Oppermann's conjecture

Last updated April 13, 2024

Unsolved problem in mathematics:

Is every pair of a square number and a pronic number (both greater than one) separated by at least one prime?

Oppermann's conjecture is an unsolved problem in mathematics on the distribution of prime numbers.^[1] It is closely related to but stronger than Legendre's conjecture, Andrica's conjecture, and Brocard's conjecture. It is named after Danish mathematician Ludvig Oppermann, who announced it in an unpublished lecture in March 1877.^[2]

Statement

The conjecture states that, for every integer x > 1, there is at least one prime number between

x(x − 1) and x²,

and at least another prime between

x² and x(x + 1).

It can also be phrased equivalently as stating that the prime-counting function must take unequal values at the endpoints of each range.^[3] That is:

π(x² − x) < π(x²) < π(x² + x) for x > 1

with π(x) being the number of prime numbers less than or equal to x. The end points of these two ranges are a square between two pronic numbers, with each of the pronic numbers being twice a pair triangular number. The sum of the pair of triangular numbers is the square.

Consequences

If the conjecture is true, then the gap size would be on the order of

g_{n}<{\sqrt {p_{n}}}\,

.

This also means there would be at least two primes between x² and (x + 1)² (one in the range from x² to x(x + 1) and the second in the range from x(x + 1) to (x + 1)²), strengthening Legendre's conjecture that there is at least one prime in this range. Because there is at least one non-prime between any two odd primes it would also imply Brocard's conjecture that there are at least four primes between the squares of consecutive odd primes.^[1] Additionally, it would imply that the largest possible gaps between two consecutive prime numbers could be at most proportional to twice the square root of the numbers, as Andrica's conjecture states.

The conjecture also implies that at least one prime can be found in every quarter revolution of the Ulam spiral.

Status

Even for small values of x, the numbers of primes in the ranges given by the conjecture are much larger than 1, providing strong evidence that the conjecture is true. However, Oppermann's conjecture has not been proved as of 2011.^[update]^[1]

Related Research Articles

<span class="mw-page-title-main">Prime number</span> Number divisible only by 1 or itself

A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, 1 × 5 or 5 × 1, involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order.

A twin prime is a prime number that is either 2 less or 2 more than another prime number—for example, either member of the twin prime pair or $(41, 43)$ . In other words, a twin prime is a prime that has a prime gap of two. Sometimes the term twin prime is used for a pair of twin primes; an alternative name for this is prime twin or prime pair.

The Ulam spiral or prime spiral is a graphical depiction of the set of prime numbers, devised by mathematician Stanisław Ulam in 1963 and popularized in Martin Gardner's Mathematical Games column in Scientific American a short time later. It is constructed by writing the positive integers in a square spiral and specially marking the prime numbers.

In number theory, an integer q is called a quadratic residue modulo n if it is congruent to a perfect square modulo n; i.e., if there exists an integer x such that:

<span class="mw-page-title-main">Bertrand's postulate</span> Existence of a prime number between any number and its double

In number theory, Bertrand's postulate is the theorem that for any integer $, there exists at least one prime number with$

In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Peter Gustav Lejeune Dirichlet's 1837 introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic progressions. It is well known for its results on prime numbers and additive number theory.

In number theory, Cramér's conjecture, formulated by the Swedish mathematician Harald Cramér in 1936, is an estimate for the size of gaps between consecutive prime numbers: intuitively, that gaps between consecutive primes are always small, and the conjecture quantifies asymptotically just how small they must be. It states that

A powerful number is a positive integer m such that for every prime number p dividing m, p² also divides m. Equivalently, a powerful number is the product of a square and a cube, that is, a number m of the form m = a²b³, where a and b are positive integers. Powerful numbers are also known as squareful, square-full, or 2-full. Paul Erdős and George Szekeres studied such numbers and Solomon W. Golomb named such numbers powerful.

Legendre's conjecture, proposed by Adrien-Marie Legendre, states that there is a prime number between $and for every positive integer . The conjecture is one of Landau's problems (1912) on prime numbers; as of 2024, the conjecture has neither been proved nor disproved.$

In number theory, Brocard's conjecture is the conjecture that there are at least four prime numbers between (p_n)² and (p_n+1)², where p_n is the n^th prime number, for every n ≥ 2. The conjecture is named after Henri Brocard. It is widely believed that this conjecture is true. However, it remains unproven as of 2022.

Euclid's theorem is a fundamental statement in number theory that asserts that there are infinitely many prime numbers. It was first proven by Euclid in his work Elements. There are several proofs of the theorem.

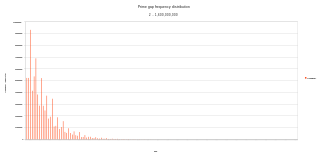
<span class="mw-page-title-main">Prime gap</span> Difference between two successive prime numbers

A prime gap is the difference between two successive prime numbers. The n-th prime gap, denoted g_n or g(p_n) is the difference between the (n + 1)-st and the n-th prime numbers, i.e.

At the 1912 International Congress of Mathematicians, Edmund Landau listed four basic problems about prime numbers. These problems were characterised in his speech as "unattackable at the present state of mathematics" and are now known as Landau's problems. They are as follows:

Goldbach's conjecture: Can every even integer greater than 2 be written as the sum of two primes?
Twin prime conjecture: Are there infinitely many primes p such that p + 2 is prime?
Legendre's conjecture: Does there always exist at least one prime between consecutive perfect squares?
Are there infinitely many primes p such that p − 1 is a perfect square? In other words: Are there infinitely many primes of the form n² + 1?

Andrica's conjecture is a conjecture regarding the gaps between prime numbers.

Brocard's problem is a problem in mathematics that seeks integer values of $such that is a perfect square, where is the factorial. Only three values of are known — 4, 5, 7 — and it is not known whether there are any more.$

In mathematics, Euler's idoneal numbers are the positive integers D such that any integer expressible in only one way as x² ± Dy² is a prime power or twice a prime power. In particular, a number that has two distinct representations as a sum of two squares is composite. Every idoneal number generates a set containing infinitely many primes and missing infinitely many other primes.

In mathematics, specifically the field of transcendental number theory, the four exponentials conjecture is a conjecture which, given the right conditions on the exponents, would guarantee the transcendence of at least one of four exponentials. The conjecture, along with two related, stronger conjectures, is at the top of a hierarchy of conjectures and theorems concerning the arithmetic nature of a certain number of values of the exponential function.

In mathematics, the Riemann hypothesis is the conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part 1/2. Many consider it to be the most important unsolved problem in pure mathematics. It is of great interest in number theory because it implies results about the distribution of prime numbers. It was proposed by Bernhard Riemann, after whom it is named.

This is a timeline of pure and applied mathematics history. It is divided here into three stages, corresponding to stages in the development of mathematical notation: a "rhetorical" stage in which calculations are described purely by words, a "syncopated" stage in which quantities and common algebraic operations are beginning to be represented by symbolic abbreviations, and finally a "symbolic" stage, in which comprehensive notational systems for formulas are the norm.

References

1 2 3 Wells, David (2011), Prime Numbers: The Most Mysterious Figures in Math, John Wiley & Sons, p. 164, ISBN 9781118045718 .
↑ Oppermann, L. (1882), "Om vor Kundskab om Primtallenes Mængde mellem givne Grændser", Oversigt over Det Kongelige Danske Videnskabernes Selskabs Forhandlinger og Dets Medlemmers Arbejder: 169–179
↑ Ribenboim, Paulo (2004), The Little Book of Bigger Primes, Springer, p. 183, ISBN 9780387201696 .

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[wells-1] 1 2 3 Wells, David (2011), Prime Numbers: The Most Mysterious Figures in Math, John Wiley & Sons, p. 164, ISBN 9781118045718 .

[2] Oppermann, L. (1882), "Om vor Kundskab om Primtallenes Mængde mellem givne Grændser", Oversigt over Det Kongelige Danske Videnskabernes Selskabs Forhandlinger og Dets Medlemmers Arbejder: 169–179

[3] Ribenboim, Paulo (2004), The Little Book of Bigger Primes, Springer, p. 183, ISBN 9780387201696 .

[1]

[2]

[3]