Related Research Articles

In a dynamical system, bistability means the system has two stable equilibrium states. Something that is bistable can be resting in either of two states. An example of a mechanical device which is bistable is a light switch. The switch lever is designed to rest in the "on" or "off" position, but not between the two. Bistable behavior can occur in mechanical linkages, electronic circuits, nonlinear optical systems, chemical reactions, and physiological and biological systems.
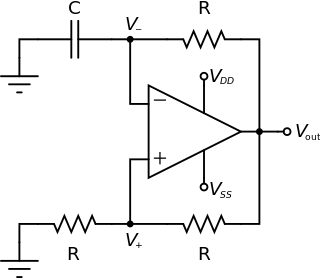
An electronic oscillator is an electronic circuit that produces a periodic, oscillating electronic signal, often a sine wave or a square wave or a triangle wave. Oscillators convert direct current (DC) from a power supply to an alternating current (AC) signal. They are widely used in many electronic devices ranging from simplest clock generators to digital instruments and complex computers and peripherals etc. Common examples of signals generated by oscillators include signals broadcast by radio and television transmitters, clock signals that regulate computers and quartz clocks, and the sounds produced by electronic beepers and video games.

Feedback occurs when outputs of a system are routed back as inputs as part of a chain of cause-and-effect that forms a circuit or loop. The system can then be said to feed back into itself. The notion of cause-and-effect has to be handled carefully when applied to feedback systems:
Simple causal reasoning about a feedback system is difficult because the first system influences the second and second system influences the first, leading to a circular argument. This makes reasoning based upon cause and effect tricky, and it is necessary to analyze the system as a whole.

Oscillation is the repetitive or periodic variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples of oscillation include a swinging pendulum and alternating current. Oscillations can be used in physics to approximate complex interactions, such as those between atoms.
The amplitude of a periodic variable is a measure of its change in a single period. The amplitude of a non-periodic signal is its magnitude compared with a reference value. There are various definitions of amplitude, which are all functions of the magnitude of the differences between the variable's extreme values. In older texts, the phase of a periodic function is sometimes called the amplitude.

In electronics a relaxation oscillator is a nonlinear electronic oscillator circuit that produces a nonsinusoidal repetitive output signal, such as a triangle wave or square wave. The circuit consists of a feedback loop containing a switching device such as a transistor, comparator, relay, op amp, or a negative resistance device like a tunnel diode, that repetitively charges a capacitor or inductor through a resistance until it reaches a threshold level, then discharges it again. The period of the oscillator depends on the time constant of the capacitor or inductor circuit. The active device switches abruptly between charging and discharging modes, and thus produces a discontinuously changing repetitive waveform. This contrasts with the other type of electronic oscillator, the harmonic or linear oscillator, which uses an amplifier with feedback to excite resonant oscillations in a resonator, producing a sine wave. Relaxation oscillators are used to produce low frequency signals for applications such as blinking lights and electronic beepers and in voltage controlled oscillators (VCOs), inverters and switching power supplies, dual-slope analog to digital converters, and function generators.

Positive feedback is a process that occurs in a feedback loop which exacerbates the effects of a small disturbance. That is, the effects of a perturbation on a system include an increase in the magnitude of the perturbation. That is, A produces more of B which in turn produces more of A. In contrast, a system in which the results of a change act to reduce or counteract it has negative feedback. Both concepts play an important role in science and engineering, including biology, chemistry, and cybernetics.

Atomic force microscopy (AFM) or scanning force microscopy (SFM) is a very-high-resolution type of scanning probe microscopy (SPM), with demonstrated resolution on the order of fractions of a nanometer, more than 1000 times better than the optical diffraction limit.
Linear electronic oscillator circuits, which generate a sinusoidal output signal, are composed of an amplifier and a frequency selective element, a filter. A linear oscillator circuit which uses an RC network, a combination of resistors and capacitors, for its frequency selective part is called an RC oscillator.
Brainwave entrainment, also referred to as brainwave synchronization or neural entrainment, refers to the observation that brainwaves will naturally synchronize to the rhythm of periodic external stimuli, such as flickering lights, speech, music, or tactile stimuli.

Neural oscillations, or brainwaves, are rhythmic or repetitive patterns of neural activity in the central nervous system. Neural tissue can generate oscillatory activity in many ways, driven either by mechanisms within individual neurons or by interactions between neurons. In individual neurons, oscillations can appear either as oscillations in membrane potential or as rhythmic patterns of action potentials, which then produce oscillatory activation of post-synaptic neurons. At the level of neural ensembles, synchronized activity of large numbers of neurons can give rise to macroscopic oscillations, which can be observed in an electroencephalogram. Oscillatory activity in groups of neurons generally arises from feedback connections between the neurons that result in the synchronization of their firing patterns. The interaction between neurons can give rise to oscillations at a different frequency than the firing frequency of individual neurons. A well-known example of macroscopic neural oscillations is alpha activity.
Nonlinear control theory is the area of control theory which deals with systems that are nonlinear, time-variant, or both. Control theory is an interdisciplinary branch of engineering and mathematics that is concerned with the behavior of dynamical systems with inputs, and how to modify the output by changes in the input using feedback, feedforward, or signal filtering. The system to be controlled is called the "plant". One way to make the output of a system follow a desired reference signal is to compare the output of the plant to the desired output, and provide feedback to the plant to modify the output to bring it closer to the desired output.
In control systems theory, the describing function (DF) method, developed by Nikolay Mitrofanovich Krylov and Nikolay Bogoliubov in the 1930s, and extended by Ralph Kochenburger is an approximate procedure for analyzing certain nonlinear control problems. It is based on quasi-linearization, which is the approximation of the non-linear system under investigation by a linear time-invariant (LTI) transfer function that depends on the amplitude of the input waveform. By definition, a transfer function of a true LTI system cannot depend on the amplitude of the input function because an LTI system is linear. Thus, this dependence on amplitude generates a family of linear systems that are combined in an attempt to capture salient features of the non-linear system behavior. The describing function is one of the few widely applicable methods for designing nonlinear systems, and is very widely used as a standard mathematical tool for analyzing limit cycles in closed-loop controllers, such as industrial process controls, servomechanisms, and electronic oscillators.
Injection locking and injection pulling are the frequency effects that can occur when a harmonic oscillator is disturbed by a second oscillator operating at a nearby frequency. When the coupling is strong enough and the frequencies near enough, the second oscillator can capture the first oscillator, causing it to have essentially identical frequency as the second. This is injection locking. When the second oscillator merely disturbs the first but does not capture it, the effect is called injection pulling. Injection locking and pulling effects are observed in numerous types of physical systems, however the terms are most often associated with electronic oscillators or laser resonators.
Recurrent thalamo-cortical resonance is an observed phenomenon of oscillatory neural activity between the thalamus and various cortical regions of the brain. It is proposed by Rodolfo Llinas and others as a theory for the integration of sensory information into the whole of perception in the brain. Thalamocortical oscillation is proposed to be a mechanism of synchronization between different cortical regions of the brain, a process known as temporal binding. This is possible through the existence of thalamocortical networks, groupings of thalamic and cortical cells that exhibit oscillatory properties.

The insulin concentration in blood increases after meals and gradually returns to basal levels during the next 1–2 hours. However, the basal insulin level is not stable. It oscillates with a regular period of 3-6 min. After a meal the amplitude of these oscillations increases but the periodicity remains constant. The oscillations are believed to be important for insulin sensitivity by preventing downregulation of insulin receptors in target cells. Such downregulation underlies insulin resistance, which is common in type 2 diabetes. It would therefore be advantageous to administer insulin to diabetic patients in a manner mimicking the natural oscillations. The insulin oscillations are generated by pulsatile release of the hormone from the pancreas. Insulin originates from beta cells located in the islets of Langerhans. Since each islet contains up to 2000 beta cells and there are one million islets in the pancreas it is apparent that pulsatile secretion requires sophisticated synchronization both within and among the islets of Langerhans.

In electronics, the Barkhausen stability criterion is a mathematical condition to determine when a linear electronic circuit will oscillate. It was put forth in 1921 by German physicist Heinrich Georg Barkhausen (1881–1956). It is widely used in the design of electronic oscillators, and also in the design of general negative feedback circuits such as op amps, to prevent them from oscillating.
Oscillators produce various levels of phase noise, or variations from perfect periodicity. Viewed as an additive noise, phase noise increases at frequencies close to the oscillation frequency or its harmonics. With the additive noise being close to the oscillation frequency, it cannot be removed by filtering without also removing the oscillation signal.
In molecular biology, an oscillating gene is a gene that is expressed in a rhythmic pattern or in periodic cycles. Oscillating genes are usually circadian and can be identified by periodic changes in the state of an organism. Circadian rhythms, controlled by oscillating genes, have a period of approximately 24 hours. For example, plant leaves opening and closing at different times of the day or the sleep-wake schedule of animals can all include circadian rhythms. Other periods are also possible, such as 29.5 days resulting from circalunar rhythms or 12.4 hours resulting from circatidal rhythms. Oscillating genes include both core clock component genes and output genes. A core clock component gene is a gene necessary for to the pacemaker. However, an output oscillating gene, such as the AVP gene, is rhythmic but not necessary to the pacemaker.
Parasitic oscillation is an undesirable electronic oscillation in an electronic or digital device. It is often caused by feedback in an amplifying device. The problem occurs notably in RF, audio, and other electronic amplifiers as well as in digital signal processing. It is one of the fundamental issues addressed by control theory.