Related Research Articles

In celestial mechanics, the Lagrange points are orbital points near two large co-orbiting bodies. Normally, the two objects exert an unbalanced gravitational force at a point, altering the orbit of whatever is at that point. At the Lagrange points, the gravitational forces of the two large bodies and the centrifugal force balance each other. This can make Lagrange points an excellent location for satellites, as few orbit corrections are needed to maintain the desired orbit. Small objects placed in orbit at Lagrange points are in equilibrium in at least two directions relative to the center of mass of the large bodies.

In physics, an orbit is the gravitationally curved trajectory of an object, such as the trajectory of a planet around a star or a natural satellite around a planet. Normally, orbit refers to a regularly repeating trajectory, although it may also refer to a non-repeating trajectory. To a close approximation, planets and satellites follow elliptic orbits, with the center of mass being orbited at a focal point of the ellipse, as described by Kepler's laws of planetary motion.

A trans-lunar injection (TLI) is a propulsive maneuver used to set a spacecraft on a trajectory that will cause it to arrive at the Moon.

Celestial mechanics is the branch of astronomy that deals with the motions of objects in outer space. Historically, celestial mechanics applies principles of physics to astronomical objects, such as stars and planets, to produce ephemeris data.

In orbital mechanics and aerospace engineering, a gravitational slingshot, gravity assist maneuver, or swing-by is the use of the relative movement and gravity of a planet or other astronomical object to alter the path and speed of a spacecraft, typically to save propellant and reduce expense.
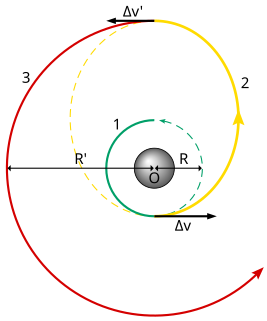
In orbital mechanics, the Hohmann transfer orbit is an elliptical orbit used to transfer between two circular orbits of different radii around a central body in the same plane. The Hohmann transfer often uses the lowest possible amount of propellant in traveling between these orbits, but bi-elliptic transfers can use less in some cases.

Orbital mechanics or astrodynamics is the application of ballistics and celestial mechanics to the practical problems concerning the motion of rockets and other spacecraft. The motion of these objects is usually calculated from Newton's laws of motion and law of universal gravitation. Orbital mechanics is a core discipline within space-mission design and control.

The Interplanetary Transport Network (ITN) is a collection of gravitationally determined pathways through the Solar System that require very little energy for an object to follow. The ITN makes particular use of Lagrange points as locations where trajectories through space can be redirected using little or no energy. These points have the peculiar property of allowing objects to orbit around them, despite lacking an object to orbit. While it would use little energy, transport along the network would take a long time.
A geocentric orbit or Earth orbit involves any object orbiting the Earth, such as the Moon or artificial satellites. In 1997 NASA estimated there were approximately 2,465 artificial satellite payloads orbiting the Earth and 6,216 pieces of space debris as tracked by the Goddard Space Flight Center. Over 16,291 previously launched objects have decayed into the Earth's atmosphere.

In astrodynamics or celestial mechanics, a hyperbolic trajectory is the trajectory of any object around a central body with more than enough speed to escape the central object's gravitational pull. The name derives from the fact that according to Newtonian theory such an orbit has the shape of a hyperbola. In more technical terms this can be expressed by the condition that the orbital eccentricity is greater than one.
In astrodynamics, the characteristic energy is a measure of the excess specific energy over that required to just barely escape from a massive body. The units are length2 time−2, i.e. velocity squared, or energy per mass.

A sphere of influence (SOI) in astrodynamics and astronomy is the oblate-spheroid-shaped region around a celestial body where the primary gravitational influence on an orbiting object is that body. This is usually used to describe the areas in the Solar System where planets dominate the orbits of surrounding objects such as moons, despite the presence of the much more massive but distant Sun. In the patched conic approximation, used in estimating the trajectories of bodies moving between the neighbourhoods of different masses using a two body approximation, ellipses and hyperbolae, the SOI is taken as the boundary where the trajectory switches which mass field it is influenced by.

Spacecraft flight dynamics is the application of mechanical dynamics to model how the external forces acting on a space vehicle or spacecraft determine its flight path. These forces are primarily of three types: propulsive force provided by the vehicle's engines; gravitational force exerted by the Earth and other celestial bodies; and aerodynamic lift and drag.

A heliocentric orbit is an orbit around the barycenter of the Solar System, which is usually located within or very near the surface of the Sun. All planets, comets, and asteroids in the Solar System, and the Sun itself are in such orbits, as are many artificial probes and pieces of debris. The moons of planets in the Solar System, by contrast, are not in heliocentric orbits, as they orbit their respective planet.

In astronomy, and in particular in astrodynamics, the osculating orbit of an object in space at a given moment in time is the gravitational Kepler orbit that it would have around its central body if perturbations were absent. That is, it is the orbit that coincides with the current orbital state vectors.

A free-return trajectory is a trajectory of a spacecraft traveling away from a primary body where gravity due to a secondary body causes the spacecraft to return to the primary body without propulsion.

Orbit determination is the estimation of orbits of objects such as moons, planets, and spacecraft. One major application is to allow tracking newly observed asteroids and verify that they have not been previously discovered. The basic methods were discovered in the 17th century and have been continuously refined.

In orbital mechanics, a Lissajous orbit, named after Jules Antoine Lissajous, is a quasi-periodic orbital trajectory that an object can follow around a Lagrangian point of a three-body system without requiring any propulsion. Lyapunov orbits around a Lagrangian point are curved paths that lie entirely in the plane of the two primary bodies. In contrast, Lissajous orbits include components in this plane and perpendicular to it, and follow a Lissajous curve. Halo orbits also include components perpendicular to the plane, but they are periodic, while Lissajous orbits are usually not.

In physics, the n-body problem is the problem of predicting the individual motions of a group of celestial objects interacting with each other gravitationally. Solving this problem has been motivated by the desire to understand the motions of the Sun, Moon, planets, and visible stars. In the 20th century, understanding the dynamics of globular cluster star systems became an important n-body problem. The n-body problem in general relativity is considerably more difficult to solve.
References
- ↑ Roger, R. Bate; Mueller, Donald D.; White, Jerry E. (1971). Fundamentals of Astrodynamics . Dover Books on Astronomy and Astrophysics. New York: Dover Publications. ISBN 0486600610. LCCN 73157430.
- ↑ Lagerstrom, P. A. and Kevorkian, J. [1963], Earth-to-moon trajectories in the restricted three-body problem, Journal de mecanique, p. 189-218.
- ↑ Koon, Wang Sang; Loo, Martin W.; Marsden, Jerrold E.; Ross, Shane D. (2011) [2005]. Dynamical Systems, the Three-Body Problem and Space Mission Design (PDF). v1.2. Marsden Books. p. 5. ISBN 978-0-615-24095-4.