Related Research Articles

In mathematics, the four color theorem, or the four color map theorem, states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color. Adjacent means that two regions share a common boundary curve segment, not merely a corner where three or more regions meet. It was the first major theorem to be proved using a computer. Initially, this proof was not accepted by all mathematicians because the computer-assisted proof was infeasible for a human to check by hand. Since then the proof has gained wide acceptance, although some doubters remain.

Thomas L. Saaty was a Distinguished University Professor at the University of Pittsburgh, where he taught in the Joseph M. Katz Graduate School of Business. He is the inventor, architect, and primary theoretician of the Analytic Hierarchy Process (AHP), a decision-making framework used for large-scale, multiparty, multi-criteria decision analysis, and of the Analytic Network Process (ANP), its generalization to decisions with dependence and feedback. Later on, he generalized the mathematics of the ANP to the Neural Network Process (NNP) with application to neural firing and synthesis but none of them gain such popularity as AHP.

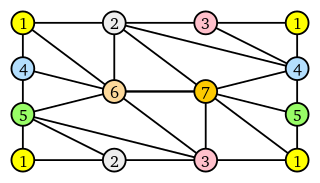
In graph theory, an edge coloring of a graph is an assignment of "colors" to the edges of the graph so that no two incident edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several different types of graph coloring. The edge-coloring problem asks whether it is possible to color the edges of a given graph using at most k different colors, for a given value of k, or with the fewest possible colors. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph. For example, the edges of the graph in the illustration can be colored by three colors but cannot be colored by two colors, so the graph shown has chromatic index three.
The Fulkerson Prize for outstanding papers in the area of discrete mathematics is sponsored jointly by the Mathematical Optimization Society (MOS) and the American Mathematical Society (AMS). Up to three awards of $1500 each are presented at each (triennial) International Symposium of the MOS. Originally, the prizes were paid out of a memorial fund administered by the AMS that was established by friends of the late Delbert Ray Fulkerson to encourage mathematical excellence in the fields of research exemplified by his work. The prizes are now funded by an endowment administered by MPS.

Frank Harary was an American mathematician, who specialized in graph theory. He was widely recognized as one of the "fathers" of modern graph theory. Harary was a master of clear exposition and, together with his many doctoral students, he standardized the terminology of graphs. He broadened the reach of this field to include physics, psychology, sociology, and even anthropology. Gifted with a keen sense of humor, Harary challenged and entertained audiences at all levels of mathematical sophistication. A particular trick he employed was to turn theorems into games - for instance, students would try to add red edges to a graph on six vertices in order to create a red triangle, while another group of students tried to add edges to create a blue triangle. Because of the theorem on friends and strangers, one team or the other would have to win.
In mathematics, the Heawood number of a surface is a certain upper bound for the maximal number of colors needed to color any graph embedded in the surface.

In graph theory, a book embedding is a generalization of planar embedding of a graph to embeddings into a book, a collection of half-planes all having the same line as their boundary. Usually, the vertices of the graph are required to lie on this boundary line, called the spine, and the edges are required to stay within a single half-plane. The book thickness of a graph is the smallest possible number of half-planes for any book embedding of the graph. Book thickness is also called pagenumber, stacknumber or fixed outerthickness. Book embeddings have also been used to define several other graph invariants including the pagewidth and book crossing number.

Arthur Leonard Rubin is an American mathematician and aerospace engineer. He was named a Putnam Fellow on four consecutive occasions from 1970 to 1973.
In graph theory, Vizing's theorem states that every simple undirected graph may be edge colored using a number of colors that is at most one larger than the maximum degree Δ of the graph. At least Δ colors are always necessary, so the undirected graphs may be partitioned into two classes: "class one" graphs for which Δ colors suffice, and "class two" graphs for which Δ + 1 colors are necessary. The theorem is named for Vadim G. Vizing who published it in 1964.
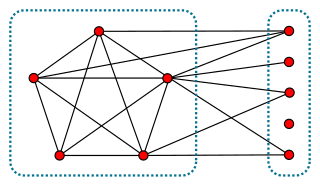
In graph theory, a branch of mathematics, a split graph is a graph in which the vertices can be partitioned into a clique and an independent set. Split graphs were first studied by Földes and Hammer, and independently introduced by Tyshkevich and Chernyak (1979).

In the mathematical field of graph theory, a graph G is said to be hypohamiltonian if G does not itself have a Hamiltonian cycle but every graph formed by removing a single vertex from G is Hamiltonian.

Maria Chudnovsky is an Israeli-American mathematician working on graph theory and combinatorial optimization. She is a 2012 MacArthur Fellow.

Gary Theodore Chartrand is an American-born mathematician who specializes in graph theory. He is known for his textbooks on introductory graph theory and for the concept of a highly irregular graph.

In the mathematical field of graph theory, the Goldner–Harary graph is a simple undirected graph with 11 vertices and 27 edges. It is named after A. Goldner and Frank Harary, who proved in 1975 that it was the smallest non-Hamiltonian maximal planar graph. The same graph had already been given as an example of a non-Hamiltonian simplicial polyhedron by Branko Grünbaum in 1967.

In the mathematical study of graph theory, a pancyclic graph is a directed graph or undirected graph that contains cycles of all possible lengths from three up to the number of vertices in the graph. Pancyclic graphs are a generalization of Hamiltonian graphs, graphs which have a cycle of the maximum possible length.
Jon Hal Folkman was an American mathematician, a student of John Milnor, and a researcher at the RAND Corporation.

In graph drawing, an arc diagram is a style of graph drawing, in which the vertices of a graph are placed along a line in the Euclidean plane, with edges being drawn as semicircles in one of the two halfplanes bounded by the line, or as smooth curves formed by sequences of semicircles. In some cases, line segments of the line itself are also allowed as edges, as long as they connect only vertices that are consecutive along the line.
In graph theory and graph drawing, a subhamiltonian graph is a subgraph of a planar Hamiltonian graph.

The Wiener–Araya graph is, in graph theory, a graph on 42 vertices with 67 edges. It is hypohamiltonian, which means that it does not itself have a Hamiltonian cycle but every graph formed by removing a single vertex from it is Hamiltonian. It is also planar.
The Beraha constants are a series of mathematical constants by which the Beraha constant is given by
References
- ↑ Mathematics faculty listing, Georgetown U., retrieved 2012-07-05.
- ↑ Saaty & Kainen (1977).
- ↑ Bernhart & Kainen (1979).
- ↑ Paul Chester Kainen at the Mathematics Genealogy Project