Related Research Articles
A twin prime is a prime number that is either 2 less or 2 more than another prime number—for example, either member of the twin prime pair or (41, 43). In other words, a twin prime is a prime that has a prime gap of two. Sometimes the term twin prime is used for a pair of twin primes; an alternative name for this is prime twin or prime pair.
The de Bruijn–Newman constant, denoted by Λ and named after Nicolaas Govert de Bruijn and Charles Michael Newman, is a mathematical constant defined via the zeros of a certain function H(λ,z), where λ is a real parameter and z is a complex variable. More precisely,

Sir William Timothy Gowers, is a British mathematician. He is Professeur titulaire of the Combinatorics chair at the Collège de France, and director of research at the University of Cambridge and Fellow of Trinity College, Cambridge. In 1998, he received the Fields Medal for research connecting the fields of functional analysis and combinatorics.
The Kepler conjecture, named after the 17th-century mathematician and astronomer Johannes Kepler, is a mathematical theorem about sphere packing in three-dimensional Euclidean space. It states that no arrangement of equally sized spheres filling space has a greater average density than that of the cubic close packing and hexagonal close packing arrangements. The density of these arrangements is around 74.05%.

In geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical size, and the space is usually three-dimensional Euclidean space. However, sphere packing problems can be generalised to consider unequal spheres, spaces of other dimensions or to non-Euclidean spaces such as hyperbolic space.
In arithmetic combinatorics, Szemerédi's theorem is a result concerning arithmetic progressions in subsets of the integers. In 1936, Erdős and Turán conjectured that every set of integers A with positive natural density contains a k-term arithmetic progression for every k. Endre Szemerédi proved the conjecture in 1975.
In mathematics, the Hales–Jewett theorem is a fundamental combinatorial result of Ramsey theory named after Alfred W. Hales and Robert I. Jewett, concerning the degree to which high-dimensional objects must necessarily exhibit some combinatorial structure; it is impossible for such objects to be "completely random".

Terence Chi-Shen Tao is an Australian mathematician. He is a professor of mathematics at the University of California, Los Angeles (UCLA), where he holds the James and Carol Collins chair. His research includes topics in harmonic analysis, partial differential equations, algebraic combinatorics, arithmetic combinatorics, geometric combinatorics, probability theory, compressed sensing and analytic number theory.

Ben Joseph Green FRS is a British mathematician, specialising in combinatorics and number theory. He is the Waynflete Professor of Pure Mathematics at the University of Oxford.
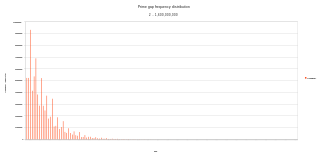
A prime gap is the difference between two successive prime numbers. The n-th prime gap, denoted gn or g(pn) is the difference between the (n + 1)-st and the n-th prime numbers, i.e.

At the 1912 International Congress of Mathematicians, Edmund Landau listed four basic problems about prime numbers. These problems were characterised in his speech as "unattackable at the present state of mathematics" and are now known as Landau's problems. They are as follows:
- Goldbach's conjecture: Can every even integer greater than 2 be written as the sum of two primes?
- Twin prime conjecture: Are there infinitely many primes p such that p + 2 is prime?
- Legendre's conjecture: Does there always exist at least one prime between consecutive perfect squares?
- Are there infinitely many primes p such that p − 1 is a perfect square? In other words: Are there infinitely many primes of the form n2 + 1?
In number theory, the Green–Tao theorem, proved by Ben Green and Terence Tao in 2004, states that the sequence of prime numbers contains arbitrarily long arithmetic progressions. In other words, for every natural number k, there exist arithmetic progressions of primes with k terms. The proof is an extension of Szemerédi's theorem. The problem can be traced back to investigations of Lagrange and Waring from around 1770.
In mathematical physics, the almost Mathieu operator arises in the study of the quantum Hall effect. It is given by
In mathematics, arithmetic combinatorics is a field in the intersection of number theory, combinatorics, ergodic theory and harmonic analysis.
In mathematics, a sign sequence, or ±1–sequence or bipolar sequence, is a sequence of numbers, each of which is either 1 or −1. One example is the sequence.

James Alexander Maynard is an English mathematician working in analytic number theory and in particular the theory of prime numbers. In 2017, he was appointed Research Professor at Oxford. Maynard is a fellow of St John's College, Oxford. He was awarded the Fields Medal in 2022 and the New Horizons in Mathematics Prize in 2023.

Tamar Debora Ziegler is an Israeli mathematician known for her work in ergodic theory, combinatorics and number theory. She holds the Henry and Manya Noskwith Chair of Mathematics at the Einstein Institute of Mathematics at the Hebrew University.

In affine geometry, a cap set is a subset of with no three elements in a line. The cap set problem is the problem of finding the size of the largest possible cap set, as a function of . The first few cap set sizes are 1, 2, 4, 9, 20, 45, 112, ....

Andrew Victor Sutherland is an American mathematician and Principal Research Scientist at the Massachusetts Institute of Technology. His research focuses on computational aspects of number theory and arithmetic geometry. He is known for his contributions to several projects involving large scale computations, including the Polymath project on bounded gaps between primes, the L-functions and Modular Forms Database, the sums of three cubes project, and the computation and classification of Sato-Tate distributions.
References
- 1 2 Nielsen, Michael (2012). Reinventing discovery: the new era of networked science . Princeton NJ: Princeton University Press. pp. 1–3. ISBN 978-0-691-14890-8.
- ↑ Gowers, Tim (27 January 2009). "Is massively collaborative mathematics possible?". Gowers' weblog. Retrieved 2009-03-30.
- ↑ Gowers, T.; Nielsen, M. (2009). "Massively collaborative mathematics". Nature. 461 (7266): 879–881. Bibcode:2009Natur.461..879G. doi:10.1038/461879a. PMID 19829354. S2CID 205050360.
- ↑ ""Crowdmath" project for high school students opens on March 1". 2 January 2016. Retrieved 18 February 2016.
- ↑ "CROWDMATH" . Retrieved 18 February 2016.
- ↑ Gowers, Tim (1 February 2009). "A combinatorial approach to density Hales-Jewett". Gower's Weblog.
- ↑ Nielsen, Michael (2009-03-20). "The Polymath project: scope of participation" . Retrieved 2009-03-30.
- ↑ Polymath (2012). "Deterministic methods to find primes". Math. Comp. 81: 1233–1246. arXiv: 1009.3956 . Bibcode:2010arXiv1009.3956P.
- ↑ Polymath (2010). "Density Hales-Jewett and Moser numbers". arXiv: 1002.0374 [math.CO].
- ↑ Polymath (2009). "A new proof of the density Hales-Jewett theorem". arXiv: 0910.3926 [math.CO].
- ↑ Polymath8 project.
- ↑ Polymath (2014). "New equidistribution estimates of Zhang type". Algebra & Number Theory. 8 (9): 2067–2199. arXiv: 1402.0811 . Bibcode:2014arXiv1402.0811P. doi:10.2140/ant.2014.8.2067. S2CID 119695637.
- ↑ Polymath (2014). "Variants of the Selberg sieve, and bounded intervals containing many primes". Research in the Mathematical Sciences. 1: 12. arXiv: 1407.4897 . Bibcode:2014arXiv1407.4897P. doi:10.1186/s40687-014-0012-7. S2CID 119699189.