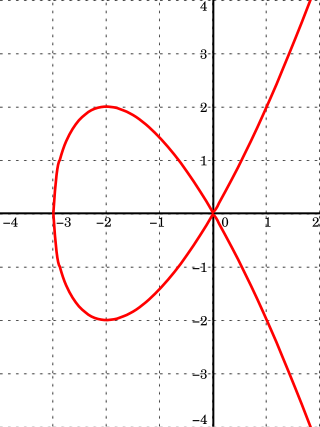In mathematics, the Chinese remainder theorem states that if one knows the remainders of the Euclidean division of an integer n by several integers, then one can determine uniquely the remainder of the division of n by the product of these integers, under the condition that the divisors are pairwise coprime.
In mathematics, a finite field or Galois field is a field that contains a finite number of elements. As with any field, a finite field is a set on which the operations of multiplication, addition, subtraction and division are defined and satisfy certain basic rules. The most common examples of finite fields are given by the integers mod p when p is a prime number.

In mathematics, an integral domain is a nonzero commutative ring in which the product of any two nonzero elements is nonzero. Integral domains are generalizations of the ring of integers and provide a natural setting for studying divisibility. In an integral domain, every nonzero element a has the cancellation property, that is, if a ≠ 0, an equality ab = ac implies b = c.
In mathematics, an irreducible polynomial is, roughly speaking, a polynomial that cannot be factored into the product of two non-constant polynomials. The property of irreducibility depends on the nature of the coefficients that are accepted for the possible factors, that is, the field to which the coefficients of the polynomial and its possible factors are supposed to belong. For example, the polynomial x2 − 2 is a polynomial with integer coefficients, but, as every integer is also a real number, it is also a polynomial with real coefficients. It is irreducible if it is considered as a polynomial with integer coefficients, but it factors as if it is considered as a polynomial with real coefficients. One says that the polynomial x2 − 2 is irreducible over the integers but not over the reals.
In mathematics, the Weil conjectures were highly influential proposals by André Weil (1949). They led to a successful multi-decade program to prove them, in which many leading researchers developed the framework of modern algebraic geometry and number theory.
Algebraic varieties are the central objects of study in algebraic geometry, a sub-field of mathematics. Classically, an algebraic variety is defined as the set of solutions of a system of polynomial equations over the real or complex numbers. Modern definitions generalize this concept in several different ways, while attempting to preserve the geometric intuition behind the original definition.
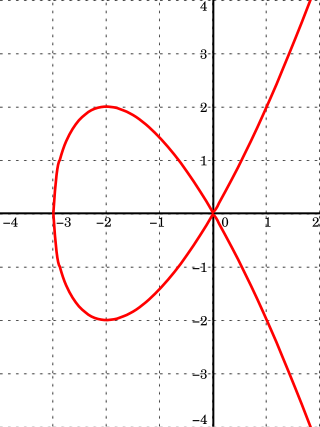
In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane curve can be completed in a projective algebraic plane curve by homogenizing its defining polynomial. Conversely, a projective algebraic plane curve of homogeneous equation h(x, y, t) = 0 can be restricted to the affine algebraic plane curve of equation h(x, y, 1) = 0. These two operations are each inverse to the other; therefore, the phrase algebraic plane curve is often used without specifying explicitly whether it is the affine or the projective case that is considered.
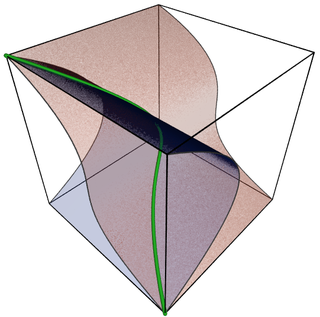
In algebraic geometry, a projective variety over an algebraically closed field k is a subset of some projective n-space over k that is the zero-locus of some finite family of homogeneous polynomials of n + 1 variables with coefficients in k, that generate a prime ideal, the defining ideal of the variety. Equivalently, an algebraic variety is projective if it can be embedded as a Zariski closed subvariety of .
Invariant theory is a branch of abstract algebra dealing with actions of groups on algebraic varieties, such as vector spaces, from the point of view of their effect on functions. Classically, the theory dealt with the question of explicit description of polynomial functions that do not change, or are invariant, under the transformations from a given linear group. For example, if we consider the action of the special linear group SLn on the space of n by n matrices by left multiplication, then the determinant is an invariant of this action because the determinant of A X equals the determinant of X, when A is in SLn.
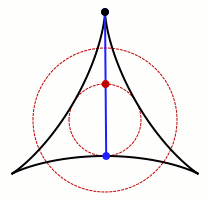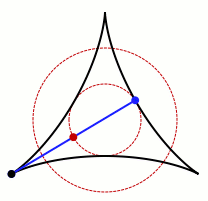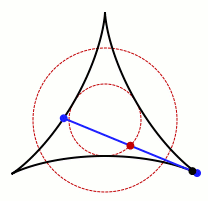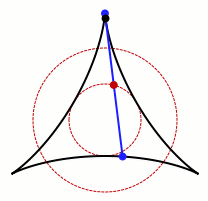
In mathematics, a Kakeya set, or Besicovitch set, is a set of points in Euclidean space which contains a unit line segment in every direction. For instance, a disk of radius 1/2 in the Euclidean plane, or a ball of radius 1/2 in three-dimensional space, forms a Kakeya set. Much of the research in this area has studied the problem of how small such sets can be. Besicovitch showed that there are Besicovitch sets of measure zero.

In mathematics, tropical geometry is the study of polynomials and their geometric properties when addition is replaced with minimization and multiplication is replaced with ordinary addition:
In mathematics, the characteristic of a ring R, often denoted char(R), is defined to be the smallest positive number of copies of the ring's multiplicative identity (1) that will sum to the additive identity (0). If no such number exists, the ring is said to have characteristic zero.
In mathematics, differential algebra is, broadly speaking, the area of mathematics consisting in the study of differential equations and differential operators as algebraic objects in view of deriving properties of differential equations and operators without computing the solutions, similarly as polynomial algebras are used for the study of algebraic varieties, which are solution sets of systems of polynomial equations. Weyl algebras and Lie algebras may be considered as belonging to differential algebra.
In mathematics and computer algebra, factorization of polynomials or polynomial factorization expresses a polynomial with coefficients in a given field or in the integers as the product of irreducible factors with coefficients in the same domain. Polynomial factorization is one of the fundamental components of computer algebra systems.
In mathematical optimization, the ellipsoid method is an iterative method for minimizing convex functions. The ellipsoid method generates a sequence of ellipsoids whose volume uniformly decreases at every step, thus enclosing a minimizer of a convex function.
In additive number theory and combinatorics, a restricted sumset has the form
In mathematics, Macdonald polynomialsPλ(x; t,q) are a family of orthogonal symmetric polynomials in several variables, introduced by Macdonald in 1987. He later introduced a non-symmetric generalization in 1995. Macdonald originally associated his polynomials with weights λ of finite root systems and used just one variable t, but later realized that it is more natural to associate them with affine root systems rather than finite root systems, in which case the variable t can be replaced by several different variables t=(t1,...,tk), one for each of the k orbits of roots in the affine root system. The Macdonald polynomials are polynomials in n variables x=(x1,...,xn), where n is the rank of the affine root system. They generalize many other families of orthogonal polynomials, such as Jack polynomials and Hall–Littlewood polynomials and Askey–Wilson polynomials, which in turn include most of the named 1-variable orthogonal polynomials as special cases. Koornwinder polynomials are Macdonald polynomials of certain non-reduced root systems. They have deep relationships with affine Hecke algebras and Hilbert schemes, which were used to prove several conjectures made by Macdonald about them.
In real algebraic geometry, Krivine–StenglePositivstellensatz characterizes polynomials that are positive on a semialgebraic set, which is defined by systems of inequalities of polynomials with real coefficients, or more generally, coefficients from any real closed field.
In ring theory, a branch of mathematics, a ring R is a polynomial identity ring if there is, for some N > 0, an element P ≠ 0 of the free algebra, Z⟨X1, X2, ..., XN⟩, over the ring of integers in N variables X1, X2, ..., XN such that
Nets Hawk Katz is the W.L. Moody Professor of Mathematics at Rice University. He was a professor of Mathematics at Indiana University Bloomington until March 2013 and the IBM Professor of Mathematics at the California Institute of Technology until 2023.