Positive polynomial

Last updated March 01, 2023

In mathematics, a positive polynomial (respectively non-negative polynomial) on a particular set is a polynomial whose values are positive (respectively non-negative) on that set. Precisely, Let p be a polynomial in n variables with real coefficients and let S be a subset of the n-dimensional Euclidean space ℝⁿ. We say that:

Positivstellensatz (and nichtnegativstellensatz)

For certain sets S, there exist algebraic descriptions of all polynomials that are positive (resp. non-negative) on S. Such a description is a positivstellensatz (resp. nichtnegativstellensatz). The importance of Positivstellensatz theorems in computation arises from its ability to transform problems of polynomial optimization into semidefinite programming problems, which can be efficiently solved using convex optimization techniques.^[1]

Examples of positivstellensatz (and nichtnegativstellensatz)

Globally positive polynomials and sum of squares decomposition.
- Every real polynomial in one variable and with even degree is non-negative on ℝ if and only if it is a sum of two squares of real polynomials in one variable.^[2] This equivalence does not generalize for polynomial with more than one variable: for instance, the Motzkin polynomial X⁴Y² + X²Y⁴ − 3X²Y² + 1 is non-negative on ℝ² but is not a sum of squares of elements from ℝ[X, Y].^[3]
- A real polynomial in n variables is non-negative on ℝⁿ if and only if it is a sum of squares of real rational functions in n variables (see Hilbert's seventeenth problem and Artin's solution^[4]).
- Suppose that p ∈ ℝ[X₁, ..., X_n] is homogeneous of even degree. If it is positive on ℝⁿ \ {0}, then there exists an integer m such that (X₁² + ... + X_n²)^m p is a sum of squares of elements from ℝ[X₁, ..., X_n].^[5]
Polynomials positive on polytopes.
- For polynomials of degree ≤ 1 we have the following variant of Farkas lemma: If f, g₁, ..., g_k have degree ≤ 1 and f(x) ≥ 0 for every x ∈ ℝⁿ satisfying g₁(x) ≥ 0, ..., g_k(x) ≥ 0, then there exist non-negative real numbers c₀, c₁, ..., c_k such that f = c₀ + c₁g₁ + ... + c_kg_k.
- Pólya's theorem:^[6] If p ∈ ℝ[X₁, ..., X_n] is homogeneous and p is positive on the set {x ∈ ℝⁿ | x₁ ≥ 0, ..., x_n ≥ 0, x₁ + ... + x_n ≠ 0}, then there exists an integer m such that (x₁ + ... + x_n)^m p has non-negative coefficients.
- Handelman's theorem:^[7] If K is a compact polytope in Euclidean d-space, defined by linear inequalities g_i ≥ 0, and if f is a polynomial in d variables that is positive on K, then f can be expressed as a linear combination with non-negative coefficients of products of members of {g_i}.
Polynomials positive on semialgebraic sets.
- The most general result is Stengle's Positivstellensatz.
- For compact semialgebraic sets we have Schmüdgen's positivstellensatz,^[8]^[9] Putinar's positivstellensatz ^[10]^[11] and Vasilescu's positivstellensatz.^[12] The point here is that no denominators are needed.
- For nice compact semialgebraic sets of low dimension, there exists a nichtnegativstellensatz without denominators.^[13]^[14]^[15]

Generalizations of positivstellensatz

Positivstellensatz also exist for signomials,^[16] trigonometric polynomials,^[17] polynomial matrices,^[18] polynomials in free variables,^[19] quantum polynomials,^[20] and definable functions on o-minimal structures.^[21]

Related Research Articles

In mathematics, a polynomial is an expression consisting of indeterminates and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. An example of a polynomial of a single indeterminate $x$ is $x 2 - 4 x + 7$ . An example with three indeterminates is $x 3 + 2 xyz 2 - yz + 1$ .

In mathematical analysis, the Weierstrass approximation theorem states that every continuous function defined on a closed interval $[a, b]$ can be uniformly approximated as closely as desired by a polynomial function. Because polynomials are among the simplest functions, and because computers can directly evaluate polynomials, this theorem has both practical and theoretical relevance, especially in polynomial interpolation. The original version of this result was established by Karl Weierstrass in 1885 using the Weierstrass transform.

Hilbert's tenth problem is the tenth on the list of mathematical problems that the German mathematician David Hilbert posed in 1900. It is the challenge to provide a general algorithm which, for any given Diophantine equation, can decide whether the equation has a solution with all unknowns taking integer values.

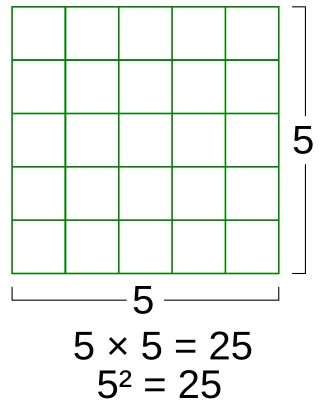
In mathematics, a square is the result of multiplying a number by itself. The verb "to square" is used to denote this operation. Squaring is the same as raising to the power 2, and is denoted by a superscript 2; for instance, the square of 3 may be written as 3², which is the number 9. In some cases when superscripts are not available, as for instance in programming languages or plain text files, the notations x^2 (caret) or x**2 may be used in place of x². The adjective which corresponds to squaring is quadratic.

In mathematics, a real closed field is a field F that has the same first-order properties as the field of real numbers. Some examples are the field of real numbers, the field of real algebraic numbers, and the field of hyperreal numbers.

In mathematics, Hilbert's fourteenth problem, that is, number 14 of Hilbert's problems proposed in 1900, asks whether certain algebras are finitely generated.

In mathematics, a homogeneous polynomial, sometimes called quantic in older texts, is a polynomial whose nonzero terms all have the same degree. For example, $is a homogeneous polynomial of degree 5, in two variables; the sum of the exponents in each term is always 5. The polynomial is not homogeneous, because the sum of exponents does not match from term to term. The function defined by a homogeneous polynomial is always a homogeneous function.$

Hilbert's seventeenth problem is one of the 23 Hilbert problems set out in a celebrated list compiled in 1900 by David Hilbert. It concerns the expression of positive definite rational functions as sums of quotients of squares. The original question may be reformulated as:

In mathematics, real algebraic geometry is the sub-branch of algebraic geometry studying real algebraic sets, i.e. real-number solutions to algebraic equations with real-number coefficients, and mappings between them.

In real algebraic geometry, Krivine–StenglePositivstellensatz characterizes polynomials that are positive on a semialgebraic set, which is defined by systems of inequalities of polynomials with real coefficients, or more generally, coefficients from any real closed field.

In real algebraic geometry, a Nash function on an open semialgebraic subset U ⊂ Rⁿ is an analytic function f: U → R satisfying a nontrivial polynomial equation P(x,f(x)) = 0 for all x in U (A semialgebraic subset of Rⁿ is a subset obtained from subsets of the form {x in Rⁿ : P(x)=0} or {x in Rⁿ : P(x) > 0}, where P is a polynomial, by taking finite unions, finite intersections and complements). Some examples of Nash functions:

In mathematics, a form (i.e. a homogeneous polynomial) h(x) of degree 2m in the real n-dimensional vector x is sum of squares of forms (SOS) if and only if there exist forms $of degree m such that$

A signomial is an algebraic function of one or more independent variables. It is perhaps most easily thought of as an algebraic extension of multivariable polynomials—an extension that permits exponents to be arbitrary real numbers while requiring the independent variables to be strictly positive.

In mathematics, the Tarski–Seidenberg theorem states that a set in (n + 1)-dimensional space defined by polynomial equations and inequalities can be projected down onto n-dimensional space, and the resulting set is still definable in terms of polynomial identities and inequalities. The theorem—also known as the Tarski–Seidenberg projection property—is named after Alfred Tarski and Abraham Seidenberg. It implies that quantifier elimination is possible over the reals, that is that every formula constructed from polynomial equations and inequalities by logical connectives $\lor$ (or), $\land$ (and), $\neg$ (not) and quantifiers $\forall$ (for all), $\exists$ (exists) is equivalent to a similar formula without quantifiers. An important consequence is the decidability of the theory of real-closed fields.

In mathematics, Hilbert spaces allow generalizing the methods of linear algebra and calculus from (finite-dimensional) Euclidean vector spaces to spaces that may be infinite-dimensional. Hilbert spaces arise naturally and frequently in mathematics and physics, typically as function spaces. Formally, a Hilbert space is a vector space equipped with an inner product that defines a distance function for which the space is a complete metric space.

In mathematics, a real number is a number that can be used to measure a continuous one-dimensional quantity such as a distance, duration or temperature. Here, continuous means that values can have arbitrarily small variations. Every real number can be almost uniquely represented by an infinite decimal expansion.

In mathematics, an invariant convex cone is a closed convex cone in a Lie algebra of a connected Lie group that is invariant under inner automorphisms. The study of such cones was initiated by Ernest Vinberg and Bertram Kostant.

This is a glossary for the terminology in a mathematical field of functional analysis.

A multivariate polynomial is SOS-convex (or sum of squares convex) if its Hessian matrix H can be factored as H(x) = S^T(x)S(x) where S is a matrix (possibly rectangular) which entries are polynomials in x. In other words, the Hessian matrix is a SOS matrix polynomial.

References

Bochnak, Jacek; Coste, Michel; Roy, Marie-Françoise. Real Algebraic Geometry. Translated from the 1987 French original. Revised by the authors. Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], 36. Springer-Verlag, Berlin, 1998. x+430 pp. ISBN 3-540-64663-9.
Marshall, Murray. "Positive polynomials and sums of squares". Mathematical Surveys and Monographs, 146. American Mathematical Society, Providence, RI, 2008. xii+187 pp. ISBN 978-0-8218-4402-1, ISBN 0-8218-4402-4.

Notes

↑ Semidefinite optimization and convex algebraic geometry. Grigoriy Blekherman, Pablo A. Parrilo, Rekha R. Thomas. Philadelphia. 2013. ISBN 978-1-61197-228-3. OCLC 809420808.{{cite book}}: CS1 maint: others (link)
↑ Benoist, Olivier (2017). "Writing Positive Polynomials as Sums of (Few) Squares". EMS Newsletter. 2017–9 (105): 8–13. doi: 10.4171/NEWS/105/4 . ISSN 1027-488X.
↑ T. S. Motzkin, The arithmetic-geometric inequality. 1967 Inequalities (Proc. Sympos. Wright-Patterson Air Force Base, Ohio, 1965) pp. 205–224.
↑ E. Artin, Uber die Zerlegung definiter Funktionen in Quadrate, Abh. Math. Sem. Univ. Hamburg, 5 (1927), 85–99.
↑ B. Reznick, Uniform denominators in Hilbert's seventeenth problem. Math. Z. 220 (1995), no. 1, 75–97.
↑ G. Pólya, Über positive Darstellung von Polynomen Vierteljschr, Naturforsch. Ges. Zürich 73 (1928) 141–145, in: R. P. Boas (Ed.), Collected Papers Vol. 2, MIT Press, Cambridge, MA, 1974, pp. 309–313.
↑ D. Handelman, Representing polynomials by positive linear functions on compact convex polyhedra. Pacific J. Math. 132 (1988), no. 1, 35–62.
↑ K. Schmüdgen. "The K-moment problem for compact semi-algebraic sets". Math. Ann. 289 (1991), no. 2, 203–206.
↑ T. Wörmann. "Strikt Positive Polynome in der Semialgebraischen Geometrie", Univ. Dortmund 1998.
↑ M. Putinar, "Positive polynomials on compact semi-algebraic sets". Indiana Univ. Math. J. 42 (1993), no. 3, 969–984.
↑ T. Jacobi, "A representation theorem for certain partially ordered commutative rings". Math. Z. 237 (2001), no. 2, 259–273.
↑ Vasilescu, F.-H. "Spectral measures and moment problems". Spectral analysis and its applications, 173–215, Theta Ser. Adv. Math., 2, Theta, Bucharest, 2003. See Theorem 1.3.1.
↑ C. Scheiderer, "Sums of squares of regular functions on real algebraic varieties". Trans. Amer. Math. Soc. 352 (2000), no. 3, 1039–1069.
↑ C. Scheiderer, "Sums of squares on real algebraic curves". Math. Z. 245 (2003), no. 4, 725–760.
↑ C. Scheiderer, "Sums of squares on real algebraic surfaces". Manuscripta Math. 119 (2006), no. 4, 395–410.
↑ Dressler, Mareike; Murray, Riley (2022-12-31). "Algebraic Perspectives on Signomial Optimization". SIAM Journal on Applied Algebra and Geometry. 6 (4): 650–684. arXiv: 2107.00345 . doi:10.1137/21M1462568. ISSN 2470-6566. S2CID 235694320.
↑ Dumitrescu, Bogdan (2007). "Positivstellensatz for Trigonometric Polynomials and Multidimensional Stability Tests". IEEE Transactions on Circuits and Systems II: Express Briefs. 54 (4): 353–356. doi:10.1109/TCSII.2006.890409. ISSN 1558-3791. S2CID 38131072.
↑ Cimprič, J. (2011). "Strict positivstellensätze for matrix polynomials with scalar constraints". Linear Algebra and Its Applications. 434 (8): 1879–1883. doi: 10.1016/j.laa.2010.11.046 . S2CID 119169153.
↑ Helton, J. William; Klep, Igor; McCullough, Scott (2012). "The convex Positivstellensatz in a free algebra". Advances in Mathematics . 231 (1): 516–534. doi: 10.1016/j.aim.2012.04.028 .
↑ Klep, Igor (2004-12-31). "The Noncommutative Graded Positivstellensatz". Communications in Algebra. 32 (5): 2029–2040. doi:10.1081/AGB-120029921. ISSN 0092-7872. S2CID 120795025.
↑ Acquistapace, F.; Andradas, C.; Broglia, F. (2002-07-01). "The Positivstellensatz for definable functions on o-minimal structures". Illinois Journal of Mathematics. 46 (3). doi: 10.1215/ijm/1258130979 . ISSN 0019-2082. S2CID 122451112.