
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted i, called the imaginary unit and satisfying the equation ; every complex number can be expressed in the form , where a and b are real numbers. Because no real number satisfies the above equation, i was called an imaginary number by René Descartes. For the complex number , a is called the real part, and b is called the imaginary part. The set of complex numbers is denoted by either of the symbols or C. Despite the historical nomenclature "imaginary", complex numbers are regarded in the mathematical sciences as just as "real" as the real numbers and are fundamental in many aspects of the scientific description of the natural world.

In mathematics, a cardinal number, or cardinal for short, is what is commonly called the number of elements of a set. In the case of a finite set, its cardinal number, or cardinality is therefore a natural number. For dealing with the case of infinite sets, the infinite cardinal numbers have been introduced, which are often denoted with the Hebrew letter (aleph) marked with subscript indicating their rank among the infinite cardinals.
In mathematics, the cardinality of a set is a measure of the number of elements of the set. For example, the set contains 3 elements, and therefore has a cardinality of 3. Beginning in the late 19th century, this concept was generalized to infinite sets, which allows one to distinguish between different types of infinity, and to perform arithmetic on them. There are two approaches to cardinality: one which compares sets directly using bijections and injections, and another which uses cardinal numbers. The cardinality of a set may also be called its size, when no confusion with other notions of size is possible.
In mathematics, especially in order theory, the cofinality cf(A) of a partially ordered set A is the least of the cardinalities of the cofinal subsets of A.
In mathematical logic, model theory is the study of the relationship between formal theories, and their models. The aspects investigated include the number and size of models of a theory, the relationship of different models to each other, and their interaction with the formal language itself. In particular, model theorists also investigate the sets that can be defined in a model of a theory, and the relationship of such definable sets to each other. As a separate discipline, model theory goes back to Alfred Tarski, who first used the term "Theory of Models" in publication in 1954. Since the 1970s, the subject has been shaped decisively by Saharon Shelah's stability theory.
In mathematics, an uncountable set is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger than aleph-null, the cardinality of the natural numbers.

In mathematics, the system of hyperreal numbers is a way of treating infinite and infinitesimal quantities. The hyperreals, or nonstandard reals, *R, are an extension of the real numbers R that contains numbers greater than anything of the form
In mathematics, transfinite numbers or infinite numbers are numbers that are "infinite" in the sense that they are larger than all finite numbers. These include the transfinite cardinals, which are cardinal numbers used to quantify the size of infinite sets, and the transfinite ordinals, which are ordinal numbers used to provide an ordering of infinite sets. The term transfinite was coined in 1895 by Georg Cantor, who wished to avoid some of the implications of the word infinite in connection with these objects, which were, nevertheless, not finite. Few contemporary writers share these qualms; it is now accepted usage to refer to transfinite cardinals and ordinals as infinite numbers. Nevertheless, the term transfinite also remains in use.
In axiomatic set theory and the branches of mathematics and philosophy that use it, the axiom of infinity is one of the axioms of Zermelo–Fraenkel set theory. It guarantees the existence of at least one infinite set, namely a set containing the natural numbers. It was first published by Ernst Zermelo as part of his set theory in 1908.
In the mathematical discipline of set theory, 0# is the set of true formulae about indiscernibles and order-indiscernibles in the Gödel constructible universe. It is often encoded as a subset of the integers, or as a subset of the hereditarily finite sets, or as a real number. Its existence is unprovable in ZFC, the standard form of axiomatic set theory, but follows from a suitable large cardinal axiom. It was first introduced as a set of formulae in Silver's 1966 thesis, later published as Silver (1971), where it was denoted by Σ, and rediscovered by Solovay, who considered it as a subset of the natural numbers and introduced the notation O#.

In mathematics, particularly in set theory, the aleph numbers are a sequence of numbers used to represent the cardinality of infinite sets that can be well-ordered. They were introduced by the mathematician Georg Cantor and are named after the symbol he used to denote them, the Hebrew letter aleph.
The von Neumann cardinal assignment is a cardinal assignment that uses ordinal numbers. For a well-orderable set U, we define its cardinal number to be the smallest ordinal number equinumerous to U, using the von Neumann definition of an ordinal number. More precisely:
In mathematics, a real closed field is a field F that has the same first-order properties as the field of real numbers. Some examples are the field of real numbers, the field of real algebraic numbers, and the field of hyperreal numbers.
PCF theory is the name of a mathematical theory, introduced by Saharon Shelah (1978), that deals with the cofinality of the ultraproducts of ordered sets. It gives strong upper bounds on the cardinalities of power sets of singular cardinals, and has many more applications as well. The abbreviation "PCF" stands for "possible cofinalities".
In mathematics, set-theoretic topology is a subject that combines set theory and general topology. It focuses on topological questions that are independent of Zermelo–Fraenkel set theory (ZFC).
Axiomatic constructive set theory is an approach to mathematical constructivism following the program of axiomatic set theory. The same first-order language with "" and "" of classical set theory is usually used, so this is not to be confused with a constructive types approach. On the other hand, some constructive theories are indeed motivated by their interpretability in type theories.

James Earl Baumgartner was an American mathematician who worked in set theory, mathematical logic and foundations, and topology.
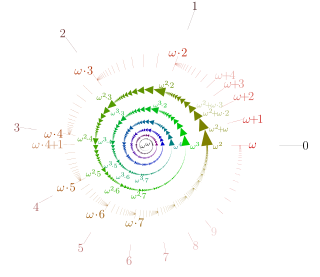
In set theory, an ordinal number, or ordinal, is a generalization of ordinal numerals aimed to extend enumeration to infinite sets.
In the mathematical discipline of set theory, a cardinal characteristic of the continuum is an infinite cardinal number that may consistently lie strictly between , and the cardinality of the continuum, that is, the cardinality of the set of all real numbers. The latter cardinal is denoted or . A variety of such cardinal characteristics arise naturally, and much work has been done in determining what relations between them are provable, and constructing models of set theory for various consistent configurations of them.




















