
An equal temperament is a musical temperament or tuning system that approximates just intervals by dividing an octave into steps such that the ratio of the frequencies of any adjacent pair of notes is the same. This system yields pitch steps perceived as equal in size, due to the logarithmic changes in pitch frequency.
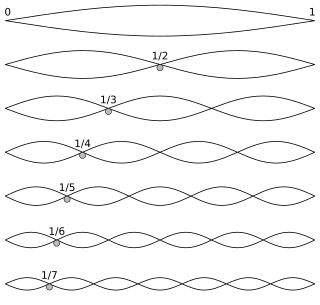
A harmonic series is the sequence of harmonics, musical tones, or pure tones whose frequency is an integer multiple of a fundamental frequency.

In music, there are two common meanings for tuning:

The piano is a keyboard instrument that produces sound when the keys are pressed. Most modern pianos have a row of 88 black and white keys: 52 white keys for the notes of the C major scale and 36 shorter black keys raised above the white keys and set further back, for sharps and flats. This means that the piano can play 88 different pitches, spanning a range of a bit over seven octaves. The black keys are for the "accidentals", which are needed to play in all twelve keys.
In music, an octave or perfect octave is a series of eight notes occupying the interval between two notes, one having twice or half the frequency of vibration of the other. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems". The interval between the first and second harmonics of the harmonic series is an octave. In Western music notation, notes separated by an octave have the same name and are of the same pitch class.
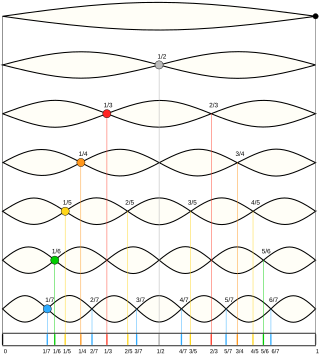
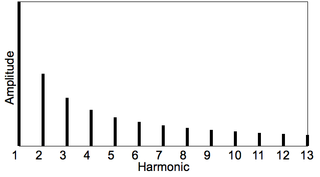
In physics, acoustics, and telecommunications, a harmonic is a sinusoidal wave with a frequency that is a positive integer multiple of the fundamental frequency of a periodic signal. The fundamental frequency is also called the 1st harmonic; the other harmonics are known as higher harmonics. As all harmonics are periodic at the fundamental frequency, the sum of harmonics is also periodic at that frequency. The set of harmonics forms a harmonic series.

An overtone is any resonant frequency above the fundamental frequency of a sound. In other words, overtones are all pitches higher than the lowest pitch within an individual sound; the fundamental is the lowest pitch. While the fundamental is usually heard most prominently, overtones are actually present in any pitch except a true sine wave. The relative volume or amplitude of various overtone partials is one of the key identifying features of timbre, or the individual characteristic of a sound.

Pitch is a perceptual property of sounds that allows their ordering on a frequency-related scale, or more commonly, pitch is the quality that makes it possible to judge sounds as "higher" and "lower" in the sense associated with musical melodies. Pitch is a major auditory attribute of musical tones, along with duration, loudness, and timbre.
In music, inharmonicity is the degree to which the frequencies of overtones depart from whole multiples of the fundamental frequency.
Piano acoustics is the set of physical properties of the piano that affect its sound. It is an area of study within musical acoustics.

Sympathetic strings or resonance strings are auxiliary strings found on many Indian musical instruments, as well as some Western Baroque instruments and a variety of folk instruments. They are typically not played directly by the performer, only indirectly through the tones that are played on the main strings, based on the principle of sympathetic resonance. The resonance is most often heard when the fundamental frequency of the string is in unison or an octave lower or higher than the catalyst note, although it can occur for other intervals, such as a fifth, with less effect.

Piano tuning is the act of adjusting the tension of the strings of an acoustic piano so that the musical intervals between strings are in tune. The meaning of the term 'in tune', in the context of piano tuning, is not simply a particular fixed set of pitches. Fine piano tuning requires an assessment of the vibration interaction among notes, which is different for every piano, thus in practice requiring slightly different pitches from any theoretical standard. Pianos are usually tuned to a modified version of the system called equal temperament.
Musical acoustics or music acoustics is a multidisciplinary field that combines knowledge from physics, psychophysics, organology, physiology, music theory, ethnomusicology, signal processing and instrument building, among other disciplines. As a branch of acoustics, it is concerned with researching and describing the physics of music – how sounds are employed to make music. Examples of areas of study are the function of musical instruments, the human voice, computer analysis of melody, and in the clinical use of music in music therapy.

In music, consonance and dissonance are categorizations of simultaneous or successive sounds. Within the Western tradition, some listeners associate consonance with sweetness, pleasantness, and acceptability, and dissonance with harshness, unpleasantness, or unacceptability, although there is broad acknowledgement that this depends also on familiarity and musical expertise. The terms form a structural dichotomy in which they define each other by mutual exclusion: a consonance is what is not dissonant, and a dissonance is what is not consonant. However, a finer consideration shows that the distinction forms a gradation, from the most consonant to the most dissonant. In casual discourse, as German composer and music theorist Paul Hindemith stressed, "The two concepts have never been completely explained, and for a thousand years the definitions have varied". The term sonance has been proposed to encompass or refer indistinctly to the terms consonance and dissonance.
Stretched tuning is a detail of musical tuning, applied to wire-stringed musical instruments, older, non-digital electric pianos, and some sample-based synthesizers based on these instruments, to accommodate the natural inharmonicity of their vibrating elements. In stretched tuning, two notes an octave apart, whose fundamental frequencies theoretically have an exact 2:1 ratio, are tuned slightly farther apart. "For a stretched tuning the octave is greater than a factor of 2; for a compressed tuning the octave is smaller than a factor of 2."

In musical tuning, a temperament is a tuning system that slightly compromises the pure intervals of just intonation to meet other requirements. Most modern Western musical instruments are tuned in the equal temperament system. Tempering is the process of altering the size of an interval by making it narrower or wider than pure. "Any plan that describes the adjustments to the sizes of some or all of the twelve fifth intervals in the circle of fifths so that they accommodate pure octaves and produce certain sizes of major thirds is called a temperament." Temperament is especially important for keyboard instruments, which typically allow a player to play only the pitches assigned to the various keys, and lack any way to alter pitch of a note in performance. Historically, the use of just intonation, Pythagorean tuning and meantone temperament meant that such instruments could sound "in tune" in one key, or some keys, but would then have more dissonance in other keys.
In music, the undertone series or subharmonic series is a sequence of notes that results from inverting the intervals of the overtone series. While overtones naturally occur with the physical production of music on instruments, undertones must be produced in unusual ways. While the overtone series is based upon arithmetic multiplication of frequencies, resulting in a harmonic series, the undertone series is based on arithmetic division.

Playing a string harmonic is a string instrument technique that uses the nodes of natural harmonics of a musical string to isolate overtones. Playing string harmonics produces high pitched tones, often compared in timbre to a whistle or flute. Overtones can be isolated "by lightly touching the string with the finger instead of pressing it down" against the fingerboard. For some instruments this is a fundamental technique, such as the Chinese guqin, where it is known as fan yin, and the Vietnamese đàn bầu.
Dynamic tonality is a paradigm for tuning and timbre which generalizes the special relationship between just intonation, and the harmonic series to apply to a wider set of pseudo-just tunings and related pseudo-harmonic timbres.

Among alternative tunings for the guitar, an overtones tuning selects its open-string notes from the overtone sequence of a fundamental note. An example is the open tuning constituted by the first six overtones of the fundamental note C, namely C2-C3-G3-C4-E4-G4.














