Related Research Articles

Category theory is a general theory of mathematical structures and their relations that was introduced by Samuel Eilenberg and Saunders Mac Lane in the middle of the 20th century in their foundational work on algebraic topology. Nowadays, category theory is used in almost all areas of mathematics, and in some areas of computer science. In particular, many constructions of new mathematical objects from previous ones, that appear similarly in several contexts are conveniently expressed and unified in terms of categories. Examples include quotient spaces, direct products, completion, and duality.

In mathematics, a category is a collection of "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose objects are sets and whose arrows are functions.
In category theory, a branch of mathematics, an initial object of a category C is an object I in C such that for every object X in C, there exists precisely one morphism I → X.
In mathematics, a complete category is a category in which all small limits exist. That is, a category C is complete if every diagram F : J → C has a limit in C. Dually, a cocomplete category is one in which all small colimits exist. A bicomplete category is a category which is both complete and cocomplete.
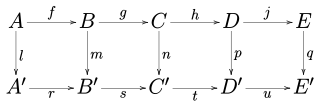
In mathematics, and especially in category theory, a commutative diagram is a diagram such that all directed paths in the diagram with the same start and endpoints lead to the same result. It is said that commutative diagrams play the role in category theory that equations play in algebra.
In category theory, a branch of mathematics, a zero morphism is a special kind of morphism exhibiting properties like the morphisms to and from a zero object.
In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous, and the identity function is continuous. The study of Top and of properties of topological spaces using the techniques of category theory is known as categorical topology.
In mathematics, especially in the field of category theory, the concept of injective object is a generalization of the concept of injective module. This concept is important in cohomology, in homotopy theory and in the theory of model categories. The dual notion is that of a projective object.
In category theory, a branch of mathematics, a pullback is the limit of a diagram consisting of two morphisms f : X → Z and g : Y → Z with a common codomain. The pullback is often written
In mathematics, a skeleton of a category is a subcategory that, roughly speaking, does not contain any extraneous isomorphisms. In a certain sense, the skeleton of a category is the "smallest" equivalent category, which captures all "categorical properties" of the original. In fact, two categories are equivalent if and only if they have isomorphic skeletons. A category is called skeletal if isomorphic objects are necessarily identical.
In mathematics, specifically in category theory, an exponential object or map object is the categorical generalization of a function space in set theory. Categories with all finite products and exponential objects are called cartesian closed categories. Categories without adjoined products may still have an exponential law.
In mathematics, a full subcategory A of a category B is said to be reflective in B when the inclusion functor from A to B has a left adjoint. This adjoint is sometimes called a reflector, or localization. Dually, A is said to be coreflective in B when the inclusion functor has a right adjoint.

In mathematics, the category Rel has the class of sets as objects and binary relations as morphisms.
In category theory, a branch of mathematics, a diagram is the categorical analogue of an indexed family in set theory. The primary difference is that in the categorical setting one has morphisms that also need indexing. An indexed family of sets is a collection of sets, indexed by a fixed set; equivalently, a function from a fixed index set to the class of sets. A diagram is a collection of objects and morphisms, indexed by a fixed category; equivalently, a functor from a fixed index category to some category.
In mathematics, a preordered class is a class equipped with a preorder.

In mathematics, the Stone functor is a functor S: Topop → Bool, where Top is the category of topological spaces and Bool is the category of Boolean algebras and Boolean homomorphisms. It assigns to each topological space X the Boolean algebra S(X) of its clopen subsets, and to each morphism fop: X → Y in Topop the homomorphism S(f): S(X) → S(Y) given by S(f)(Z) = f−1[Z].
In the mathematical field of category theory, an amnestic functorF : A → B is a functor for which an A-isomorphism ƒ is an identity whenever Fƒ is an identity.
In mathematics, particularly in category theory, a morphism is a structure-preserving map from one mathematical structure to another one of the same type. The notion of morphism recurs in much of contemporary mathematics. In set theory, morphisms are functions; in linear algebra, linear transformations; in group theory, group homomorphisms; in topology, continuous functions, and so on.
In mathematics, in the framework of one-universe foundation for category theory, the term "conglomerate" is applied to arbitrary sets as a contraposition to the distinguished sets that are elements of a Grothendieck universe.

Horst Herrlich was a German mathematician, known as a pioneer of categorical topology.
References
- Adámek, Jiří, Herrlich, Horst, & Strecker, George E. (1990). Abstract and Concrete Categories (4.2MB PDF). Originally publ. John Wiley & Sons. ISBN 0-471-60922-6. (now free on-line edition)
- Herrlich, Horst, & Strecker, George E., Category Theory, Heldermann Verlag (2007).