 | This article may be too technical for most readers to understand.(September 2010) |
In mathematics, a quantaloid is a category enriched over the category Sup of suplattices . [1] In other words, for any objects a and b the morphism object between them is not just a set but a complete lattice, in such a way that composition of morphisms preserves all joins:
The endomorphism lattice of any object in a quantaloid is a quantale, whence the name.
In mathematics, specifically category theory, a functor is a mapping between categories. Functors were first considered in algebraic topology, where algebraic objects are associated to topological spaces, and maps between these algebraic objects are associated to continuous maps between spaces. Nowadays, functors are used throughout modern mathematics to relate various categories. Thus, functors are important in all areas within mathematics to which category theory is applied.
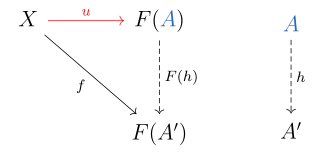
In category theory, a branch of mathematics, a universal property is an important property which is satisfied by a universal morphism. Universal morphisms can also be thought of more abstractly as initial or terminal objects of a comma category. Universal properties occur almost everywhere in mathematics, and hence the precise category theoretic concept helps point out similarities between different branches of mathematics, some of which may even seem unrelated.
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products, pullbacks and inverse limits. The dual notion of a colimit generalizes constructions such as disjoint unions, direct sums, coproducts, pushouts and direct limits.
In mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum (join) and an infimum (meet). Specifically, every non-empty finite lattice is complete. Complete lattices appear in many applications in mathematics and computer science. Being a special instance of lattices, they are studied both in order theory and universal algebra.
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed, this intuition can be formalized to define so-called functor categories. Natural transformations are, after categories and functors, one of the most fundamental notions of category theory and consequently appear in the majority of its applications.
In mathematics, specifically category theory, adjunction is a relationship that two functors may have. Two functors that stand in this relationship are known as adjoint functors, one being the left adjoint and the other the right adjoint. Pairs of adjoint functors are ubiquitous in mathematics and often arise from constructions of "optimal solutions" to certain problems, such as the construction of a free group on a set in algebra, or the construction of the Stone–Čech compactification of a topological space in topology.
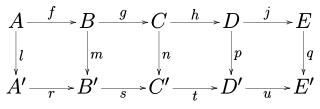
In mathematics, and especially in category theory, a commutative diagram is a diagram such that all directed paths in the diagram with the same start and endpoints lead to the same result. It is said that commutative diagrams play the role in category theory that equations play in algebra.
In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the Cartesian product of sets, the direct product of groups or rings, and the product of topological spaces. Essentially, the product of a family of objects is the "most general" object which admits a morphism to each of the given objects.
In mathematics, a Heyting algebra is a bounded lattice equipped with a binary operation a → b of implication such that ≤ b is equivalent to c ≤. From a logical standpoint, A → B is by this definition the weakest proposition for which modus ponens, the inference rule A → B, A ⊢ B, is sound. Like Boolean algebras, Heyting algebras form a variety axiomatizable with finitely many equations. Heyting algebras were introduced by Arend Heyting (1930) to formalize intuitionistic logic.
In category theory, a branch of mathematics, duality is a correspondence between the properties of a category C and the dual properties of the opposite category Cop. Given a statement regarding the category C, by interchanging the source and target of each morphism as well as interchanging the order of composing two morphisms, a corresponding dual statement is obtained regarding the opposite category Cop. Duality, as such, is the assertion that truth is invariant under this operation on statements. In other words, if a statement is true about C, then its dual statement is true about Cop. Also, if a statement is false about C, then its dual has to be false about Cop.
In category theory, a branch of mathematics, a monad is an endofunctor, together with two natural transformations required to fulfill certain coherence conditions. Monads are used in the theory of pairs of adjoint functors, and they generalize closure operators on partially ordered sets to arbitrary categories.
In category theory, a branch of abstract mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics. Establishing an equivalence involves demonstrating strong similarities between the mathematical structures concerned. In some cases, these structures may appear to be unrelated at a superficial or intuitive level, making the notion fairly powerful: it creates the opportunity to "translate" theorems between different kinds of mathematical structures, knowing that the essential meaning of those theorems is preserved under the translation.
In mathematics, especially in the field of category theory, the concept of injective object is a generalization of the concept of injective module. This concept is important in cohomology, in homotopy theory and in the theory of model categories. The dual notion is that of a projective object.
In mathematics, especially in order theory, a complete Heyting algebra is a Heyting algebra that is complete as a lattice. Complete Heyting algebras are the objects of three different categories; the category CHey, the category Loc of locales, and its opposite, the category Frm of frames. Although these three categories contain the same objects, they differ in their morphisms, and thus get distinct names. Only the morphisms of CHey are homomorphisms of complete Heyting algebras.
In mathematics, quantales are certain partially ordered algebraic structures that generalize locales as well as various multiplicative lattices of ideals from ring theory and functional analysis. Quantales are sometimes referred to as complete residuated semigroups.
In mathematics, specifically in category theory, an exponential object or map object is the categorical generalization of a function space in set theory. Categories with all finite products and exponential objects are called cartesian closed categories. Categories without adjoined products may still have an exponential law.
This is a glossary of properties and concepts in category theory in mathematics.
In category theory, a Kleisli category is a category naturally associated to any monad T. It is equivalent to the category of free T-algebras. The Kleisli category is one of two extremal solutions to the question Does every monad arise from an adjunction? The other extremal solution is the Eilenberg–Moore category. Kleisli categories are named for the mathematician Heinrich Kleisli.
In the mathematical area of order theory, a completely distributive lattice is a complete lattice in which arbitrary joins distribute over arbitrary meets.
In mathematics, in the area of order theory, a free lattice is the free object corresponding to a lattice. As free objects, they have the universal property.
 | This category theory-related article is a stub. You can help Wikipedia by expanding it. |
