Bra–ket notation, also called Dirac notation, is a notation for linear algebra and linear operators on complex vector spaces together with their dual space both in the finite-dimensional and infinite-dimensional case. It is specifically designed to ease the types of calculations that frequently come up in quantum mechanics. Its use in quantum mechanics is quite widespread.
Shor's algorithm is a quantum algorithm for finding the prime factors of an integer. It was developed in 1994 by the American mathematician Peter Shor. It is one of the few known quantum algorithms with compelling potential applications and strong evidence of superpolynomial speedup compared to best known classical algorithms. On the other hand, factoring numbers of practical significance requires far more qubits than available in the near future. Another concern is that noise in quantum circuits may undermine results, requiring additional qubits for quantum error correction.

Quantum superposition is a fundamental principle of quantum mechanics that states that linear combinations of solutions to the Schrödinger equation are also solutions of the Schrödinger equation. This follows from the fact that the Schrödinger equation is a linear differential equation in time and position. More precisely, the state of a system is given by a linear combination of all the eigenfunctions of the Schrödinger equation governing that system.

Quantum decoherence is the loss of quantum coherence. Quantum decoherence has been studied to understand how quantum systems convert to systems which can be explained by classical mechanics. Beginning out of attempts to extend the understanding of quantum mechanics, the theory has developed in several directions and experimental studies have confirmed some of the key issues. Quantum computing relies on quantum coherence and is the primary practical applications of the concept.
In physics, an operator is a function over a space of physical states onto another space of physical states. The simplest example of the utility of operators is the study of symmetry. Because of this, they are useful tools in classical mechanics. Operators are even more important in quantum mechanics, where they form an intrinsic part of the formulation of the theory.

In quantum mechanics, a probability amplitude is a complex number used for describing the behaviour of systems. The square of the modulus of this quantity represents a probability density.

In quantum mechanics and computing, the Bloch sphere is a geometrical representation of the pure state space of a two-level quantum mechanical system (qubit), named after the physicist Felix Bloch.
In quantum computing and specifically the quantum circuit model of computation, a quantum logic gate is a basic quantum circuit operating on a small number of qubits. Quantum logic gates are the building blocks of quantum circuits, like classical logic gates are for conventional digital circuits.
In quantum information theory, a quantum channel is a communication channel which can transmit quantum information, as well as classical information. An example of quantum information is the state of a qubit. An example of classical information is a text document transmitted over the Internet.

In quantum mechanics, a two-state system is a quantum system that can exist in any quantum superposition of two independent quantum states. The Hilbert space describing such a system is two-dimensional. Therefore, a complete basis spanning the space will consist of two independent states. Any two-state system can also be seen as a qubit.

LOCC, or local operations and classical communication, is a method in quantum information theory where a local (product) operation is performed on part of the system, and where the result of that operation is "communicated" classically to another part where usually another local operation is performed conditioned on the information received.
In category theory, a branch of mathematics, dagger compact categories first appeared in 1989 in the work of Sergio Doplicher and John E. Roberts on the reconstruction of compact topological groups from their category of finite-dimensional continuous unitary representations. They also appeared in the work of John Baez and James Dolan as an instance of semistrict k-tuply monoidal n-categories, which describe general topological quantum field theories, for n = 1 and k = 3. They are a fundamental structure in Samson Abramsky and Bob Coecke's categorical quantum mechanics.
Amplitude amplification is a technique in quantum computing which generalizes the idea behind Grover's search algorithm, and gives rise to a family of quantum algorithms. It was discovered by Gilles Brassard and Peter Høyer in 1997, and independently rediscovered by Lov Grover in 1998.
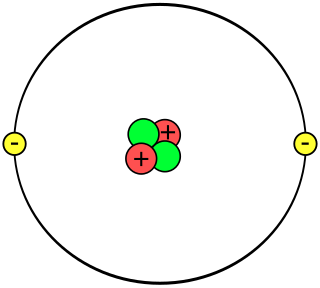
A helium atom is an atom of the chemical element helium. Helium is composed of two electrons bound by the electromagnetic force to a nucleus containing two protons along with two neutrons, depending on the isotope, held together by the strong force. Unlike for hydrogen, a closed-form solution to the Schrödinger equation for the helium atom has not been found. However, various approximations, such as the Hartree–Fock method, can be used to estimate the ground state energy and wavefunction of the atom. Historically, the first such helium spectrum calculation was done by Albrecht Unsöld in 1927. Its success was considered to be one of the earliest signs of validity of Schrödinger's wave mechanics.
Entanglement distillation is the transformation of N copies of an arbitrary entangled state into some number of approximately pure Bell pairs, using only local operations and classical communication.
In quantum computing, the quantum phase estimation algorithm is a quantum algorithm to estimate the phase corresponding to an eigenvalue of a given unitary operator. Because the eigenvalues of a unitary operator always have unit modulus, they are characterized by their phase, and therefore the algorithm can be equivalently described as retrieving either the phase or the eigenvalue itself. The algorithm was initially introduced by Alexei Kitaev in 1995.
In quantum physics, a quantum state is a mathematical entity that embodies the knowledge of a quantum system. Quantum mechanics specifies the construction, evolution, and measurement of a quantum state. The result is a quantum-mechanical prediction for the system represented by the state. Knowledge of the quantum state, and the quantum mechanical rules for the system's evolution in time, exhausts all that can be known about a quantum system.
In quantum mechanics, weak measurements are a type of quantum measurement that results in an observer obtaining very little information about the system on average, but also disturbs the state very little. From Busch's theorem the system is necessarily disturbed by the measurement. In the literature weak measurements are also known as unsharp, fuzzy, dull, noisy, approximate, and gentle measurements. Additionally weak measurements are often confused with the distinct but related concept of the weak value.
In quantum computation, the Hadamard test is a method used to create a random variable whose expected value is the expected real part , where is a quantum state and is a unitary gate acting on the space of . The Hadamard test produces a random variable whose image is in and whose expected value is exactly . It is possible to modify the circuit to produce a random variable whose expected value is by applying an gate after the first Hadamard gate.
Many-body localization (MBL) is a dynamical phenomenon which leads to the breakdown of equilibrium statistical mechanics in isolated many-body systems. Such systems never reach local thermal equilibrium, and retain local memory of their initial conditions for infinite times. One can still define a notion of phase structure in these out-of-equilibrium systems. Strikingly, MBL can even enable new kinds of exotic orders that are disallowed in thermal equilibrium – a phenomenon that goes by the name of localization-protected quantum order (LPQO) or eigenstate order.
















































