Random utility model

Last updated

In economics and psychology, a random utility model, [1] [2] also called stochastic utility model, [3] is a mathematical description of the preferences of a person, whose choices are not deterministic, but depend on a random state variable.

Contents

Background

A basic assumption in classic economics is that the choices of a rational person choices are guided by a preference relation, which can usually be described by a utility function. When faced with several alternatives, the person will choose the alternative with the highest utility. The utility function is not visible; however, by observing the choices made by the person, we can "reverse-engineer" his utility function. This is the goal of revealed preference theory.

In practice, however, people are not rational. Ample empirical evidence shows that, when faced with the same set of alternatives, people may make different choices. [4] [5] [6] [7] [8] To an outside observer, their choices may appear random.

One way to model this behavior is called stochastic rationality. It is assumed that each agent has an unobserved state, which can be considered a random variable. Given that state, the agent behaves rationally. In other words: each agent has, not a single preference-relation, but a distribution over preference-relations (or utility functions).

The representation problem

Block and Marschak [9] presented the following problem. Suppose we are given as input, a set of choice probabilitiesPa,B, describing the probability that an agent chooses alternative a from the set B. We want to rationalize the agent's behavior by a probability distribution over preference relations. That is: we want to find a distribution such that, for all pairs a,B given in the input, Pa,B = Prob[a is weakly preferred to all alternatives in B]. What conditions on the set of probabilities Pa,B guarantee the existence of such a distribution?

Falmagne [10] solved this problem for the case in which the set of alternatives is finite: he proved that a probability distribution exists iff a set of polynomials derived from the choice-probabilities, denoted Block-Marschak polynomials, are nonnegative. His solution is constructive, and provides an algorithm for computing the distribution.

Barbera and Pattanaik [11] extend this result to settings in which the agent may choose sets of alternatives, rather than just singletons.

Uniqueness

Block and Marschak [9] proved that, when there are at most 3 alternatives, the random utility model is unique ("identified"); however, when there are 4 or more alternatives, the model may be non-unique. [11] For example, [12] we can compute the probability that the agent prefers w to x (w>x), and the probability that y>z, but may not be able to know the probability that both w>x and y>z. There are even distributions with disjoint supports, which induce the same set of choice probabilities.

Some conditions for uniqueness were given by Falmagne. [10] Turansick [13] presents two characterizations for the existence of a unique random utility representation.

Models

There are various random utility models, which differ in the assumptions on the probability distributions of the agent's utility, A popular random utility model was developed by Luce [14] and Plackett. [15] They assume that the random utility terms are generated according to Gumbel distributions with fixed shape parameter. In the Plackett–Luce model, the likelihood function has a simple analytical solution, so maximum likelihood estimation can be done in polynomial time.

The Plackett–Luce model was applied in econometrics, [16] for example, to analyze automobile prices in market equilibrium. [17] It was also applied in machine learning and information retrieval. [18] It was also applied in social choice, to analyze an opinion poll conducted during the Irish presidential election. [19] Efficient methods for expectation–maximization and expectation propagation exist for the Plackett–Luce model. [20] [21] [22]

Azari, Parkes and Xia [23] extend the Plackett–Luce model: they consider random utility models in which the random utilities can be drawn from any distribution in the Exponential family. They prove conditions under which the log-likelihood function is concave, and the set of global maxima solutions is bounded for a family of random utility models where the shape of each distribution is fixed and the only latent variables are the means.

Application to social choice

Random utility models can be used not only for modeling the behavior of a single agent, but also for decision-making among a society of agents. [23] One approach to social choice, first formalized by Condorcet's jury theorem, is that there is a "ground truth" – a true ranking of the alternatives. Each agent in society receives a noisy signal of this true ranking. The best way to approach the ground truth is using maximum likelihood estimation: construct a social ranking which maximizes the likelihood of the set of individual rankings.

Condorcet's original model assumes that the probabilities of agents' mistakes in pairwise comparisons are independent and identically distributed: all mistakes have the same probability p. This model has several drawbacks:

Random utility models provides an alternative: there is a ground-truth vector of utilities; each agent draws a utility for each alternative, based on a probability distribution whose mean value is the ground-truth. This model captures the strength of preferences, and rules out cyclic preferences. Moreover, for some common probability distributions (particularly, the Plackett–Luce model), the maximum likelihood estimators can be computed efficiently.

Generalizations

Walker and Ben-Akiva [25] generalize the classic random utility model in several ways, aiming to improve the accuracy of forecasts:

Blavatzkyy [26] studies stochastic utility theory based on choices between lotteries. The input is a set of choice probabilities, which indicate the likelihood that the agent choose one lottery over the other. The desired output is a stochastic utility representation: a writing of the choice probabilities as a non-decreasing function of the difference in expected utilities of the lotteries. He proves that choice probabilities admit a stochastic utility representation iff they are complete, strongly transitive, continuous, independent of common consequences, and interchangeable.

Related Research Articles

Independence of irrelevant alternatives (IIA), also known as binary independence, the independence axiom, is an axiom of decision theory and economics describing a necessary condition for rational behavior. The axiom says that a choice between and should not depend on the quality of a third, unrelated outcome .

The expected utility hypothesis is a foundational assumption in mathematical economics concerning decision making under uncertainty. It postulates that rational agents maximize utility, meaning the subjective desirability of their actions. Rational choice theory, a cornerstone of microeconomics, builds this postulate to model aggregate social behaviour.

In statistics, the method of moments is a method of estimation of population parameters. The same principle is used to derive higher moments like skewness and kurtosis.

The Allais paradox is a choice problem designed by Maurice Allais to show an inconsistency of actual observed choices with the predictions of expected utility theory. Rather than adhering to rationality, the Allais paradox proves that individuals rarely make rational decisions consistently when required to do so immediately. The independence axiom of expected utility theory, which requires that the preferences of an individual should not change when altering two lotteries by equal proportions, was proven to be violated by the paradox.

<span class="mw-page-title-main">Jacob Marschak</span> American economist (1898-1977)

Jacob Marschak was an American economist.

In economics, discrete choice models, or qualitative choice models, describe, explain, and predict choices between two or more discrete alternatives, such as entering or not entering the labor market, or choosing between modes of transport. Such choices contrast with standard consumption models in which the quantity of each good consumed is assumed to be a continuous variable. In the continuous case, calculus methods can be used to determine the optimum amount chosen, and demand can be modeled empirically using regression analysis. On the other hand, discrete choice analysis examines situations in which the potential outcomes are discrete, such that the optimum is not characterized by standard first-order conditions. Thus, instead of examining "how much" as in problems with continuous choice variables, discrete choice analysis examines "which one". However, discrete choice analysis can also be used to examine the chosen quantity when only a few distinct quantities must be chosen from, such as the number of vehicles a household chooses to own and the number of minutes of telecommunications service a customer decides to purchase. Techniques such as logistic regression and probit regression can be used for empirical analysis of discrete choice.

Quantal response equilibrium (QRE) is a solution concept in game theory. First introduced by Richard McKelvey and Thomas Palfrey, it provides an equilibrium notion with bounded rationality. QRE is not an equilibrium refinement, and it can give significantly different results from Nash equilibrium. QRE is only defined for games with discrete strategies, although there are continuous-strategy analogues.

In economics, and in other social sciences, preference refers to an order by which an agent, while in search of an "optimal choice", ranks alternatives based on their respective utility. Preferences are evaluations that concern matters of value, in relation to practical reasoning. Individual preferences are determined by taste, need, ..., as opposed to price, availability or personal income. Classical economics assumes that people act in their best (rational) interest. In this context, rationality would dictate that, when given a choice, an individual will select an option that maximizes their self-interest. But preferences are not always transitive, both because real humans are far from always being rational and because in some situations preferences can form cycles, in which case there exists no well-defined optimal choice. An example of this is Efron dice.

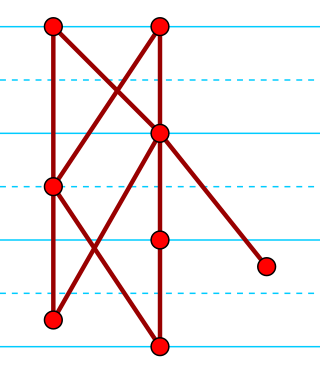
<span class="mw-page-title-main">Semiorder</span> Numerical ordering with a margin of error

In order theory, a branch of mathematics, a semiorder is a type of ordering for items with numerical scores, where items with widely differing scores are compared by their scores and where scores within a given margin of error are deemed incomparable. Semiorders were introduced and applied in mathematical psychology by Duncan Luce as a model of human preference. They generalize strict weak orderings, in which items with equal scores may be tied but there is no margin of error. They are a special case of partial orders and of interval orders, and can be characterized among the partial orders by additional axioms, or by two forbidden four-item suborders.

<span class="mw-page-title-main">Jean-Claude Falmagne</span>

Jean-Claude Falmagne is a mathematical psychologist whose scientific contributions deal with problems in reaction time theory, psychophysics, philosophy of science, measurement theory, decision theory, and educational technology. Together with Jean-Paul Doignon, he developed knowledge space theory, which is the mathematical foundation for the ALEKS software for the assessment of knowledge in various academic subjects, including K-12 mathematics, chemistry, and accounting.

<span class="mw-page-title-main">Jean-François Mertens</span> Belgian game theorist (1946–2012)

Jean-François Mertens was a Belgian game theorist and mathematical economist.

Maximal lotteries are a tournament voting rule that elects the majority-preferred candidate if one exists, and otherwise elects a candidate from the majority-preferred set by a randomized voting procedure. The method selects the probability distribution of candidates that a majority of voters would prefer to any other.

Fair random assignment is a kind of a fair division problem.

Random priority (RP), also called Random serial dictatorship (RSD), is a procedure for fair random assignment - dividing indivisible items fairly among people.

A simultaneous eating algorithm(SE) is an algorithm for allocating divisible objects among agents with ordinal preferences. "Ordinal preferences" means that each agent can rank the items from best to worst, but cannot (or does not want to) specify a numeric value for each item. The SE allocation satisfies SD-efficiency - a weak ordinal variant of Pareto-efficiency (it means that the allocation is Pareto-efficient for at least one vector of additive utility functions consistent with the agents' item rankings).


A major branch of social choice theory is devoted to the comparison of electoral systems, otherwise known as social choice functions. Viewed from the perspective of political science, electoral systems are rules for conducting elections and determining winners from the ballots cast. From the perspective of economics, mathematics, and philosophy, a social choice function is a mathematical function that determines how a society should make choices, given a collection of individual preferences.

Impartial culture (IC) or the culture of indifference is a probabilistic model used in social choice theory for analyzing ranked voting method rules.

Stochastic transitivity models are stochastic versions of the transitivity property of binary relations studied in mathematics. Several models of stochastic transitivity exist and have been used to describe the probabilities involved in experiments of paired comparisons, specifically in scenarios where transitivity is expected, however, empirical observations of the binary relation is probabilistic. For example, players' skills in a sport might be expected to be transitive, i.e. "if player A is better than B and B is better than C, then player A must be better than C"; however, in any given match, a weaker player might still end up winning with a positive probability. Tightly matched players might have a higher chance of observing this inversion while players with large differences in their skills might only see these inversions happen seldom. Stochastic transitivity models formalize such relations between the probabilities and the underlying transitive relation.

Fractional social choice is a branch of social choice theory in which the collective decision is not a single alternative, but rather a weighted sum of two or more alternatives. For example, if society has to choose between three candidates: A B or C, then in standard social choice, exactly one of these candidates is chosen, while in fractional social choice, it is possible to choose "2/3 of A and 1/3 of B".

References

  1. ↑ Manski, Charles F. (July 1977). "The structure of random utility models". Theory and Decision. 8 (3): 229–254. doi:10.1007/BF00133443. S2CID   120718598. ProQuest   1303217712.
  2. ↑ Cascetta, Ennio (2009). "Random Utility Theory". Transportation Systems Analysis. Springer Optimization and Its Applications. Vol. 29. pp. 89–167. doi:10.1007/978-0-387-75857-2_3. ISBN   978-0-387-75856-5.
  3. ↑ Manski, Charles F. (August 1975). "Maximum score estimation of the stochastic utility model of choice". Journal of Econometrics. 3 (3): 205–228. doi:10.1016/0304-4076(75)90032-9.
  4. ↑ Camerer, Colin F. (April 1989). "An experimental test of several generalized utility theories". Journal of Risk and Uncertainty. 2 (1): 61–104. doi:10.1007/BF00055711. S2CID   154335530.
  5. ↑ Starmer, Chris; Sugden, Robert (June 1989). "Probability and juxtaposition effects: An experimental investigation of the common ratio effect". Journal of Risk and Uncertainty. 2 (2): 159–178. doi:10.1007/BF00056135. S2CID   153567599.
  6. ↑ Hey, John D.; Orme, Chris (1994). "Investigating Generalizations of Expected Utility Theory Using Experimental Data". Econometrica. 62 (6): 1291–1326. doi:10.2307/2951750. JSTOR   2951750. S2CID   120069179.
  7. ↑ Wu, George (1994). "An empirical test of ordinal independence". Journal of Risk and Uncertainty. 9 (1): 39–60. doi:10.1007/BF01073402. S2CID   153558846.
  8. ↑ Ballinger, T. Parker; Wilcox, Nathaniel T. (July 1997). "Decisions, Error and Heterogeneity". The Economic Journal. 107 (443): 1090–1105. doi:10.1111/j.1468-0297.1997.tb00009.x. S2CID   153823510.
  9. 1 2 Block, H. D. (1974). "Random Orderings and Stochastic Theories of Responses (1960)". Economic Information, Decision, and Prediction. pp. 172–217. doi:10.1007/978-94-010-9276-0_8. ISBN   978-90-277-1195-3.
  10. 1 2 Falmagne, J.C. (August 1978). "A representation theorem for finite random scale systems". Journal of Mathematical Psychology. 18 (1): 52–72. doi:10.1016/0022-2496(78)90048-2.
  11. 1 2 Barberá, Salvador; Pattanaik, Prasanta K. (1986). "Falmagne and the Rationalizability of Stochastic Choices in Terms of Random Orderings". Econometrica. 54 (3): 707–715. doi:10.2307/1911317. JSTOR   1911317.
  12. ↑ https://scholar.harvard.edu/files/tomasz/files/lisbon32-post.pdf%5B%5D%5B%5D
  13. ↑ Turansick, Christopher (July 2022). "Identification in the random utility model". Journal of Economic Theory. 203: 105489. arXiv: 2102.05570 . doi:10.1016/j.jet.2022.105489. S2CID   231861383.
  14. ↑ Luce, R. Duncan (2012). Individual Choice Behavior: A Theoretical Analysis. Courier Corporation. ISBN   978-0-486-15339-1.[ page needed ]
  15. ↑ Plackett, R. L. (1975). "The Analysis of Permutations". Applied Statistics. 24 (2): 193–202. doi:10.2307/2346567. JSTOR   2346567.
  16. ↑ McFadden, Daniel (1974). "Conditional Logit Analysis of Qualitative Choice Behavior". In Zarembka, Paul (ed.). Frontiers in Econometrics. Academic Press. pp. 105–142. ISBN   978-0-12-776150-3.
  17. ↑ Berry, Steven; Levinsohn, James; Pakes, Ariel (1995). "Automobile Prices in Market Equilibrium". Econometrica. 63 (4): 841–890. doi:10.2307/2171802. JSTOR   2171802.
  18. ↑ Liu, Tie-Yan (2007). "Learning to Rank for Information Retrieval". Foundations and Trends in Information Retrieval. 3 (3): 225–331. doi:10.1561/1500000016.
  19. ↑ Gormley, Isobel Claire; Murphy, Thomas Brendan (June 2009). "A grade of membership model for rank data". Bayesian Analysis. 4 (2). doi: 10.1214/09-BA410 . hdl: 10197/7121 . S2CID   53559452.
  20. ↑ Caron, François; Doucet, Arnaud (January 2012). "Efficient Bayesian Inference for Generalized Bradley–Terry Models". Journal of Computational and Graphical Statistics. 21 (1): 174–196. arXiv: 1011.1761 . doi:10.1080/10618600.2012.638220. S2CID   42955305.
  21. ↑ Hunter, David R. (February 2004). "MM algorithms for generalized Bradley-Terry models". The Annals of Statistics. 32 (1). doi: 10.1214/aos/1079120141 .
  22. ↑ Guiver, John; Snelson, Edward (2009). "Bayesian inference for Plackett–Luce ranking models". Proceedings of the 26th Annual International Conference on Machine Learning. pp. 377–384. doi:10.1145/1553374.1553423. ISBN   978-1-60558-516-1. S2CID   16965626.
  23. 1 2 Azari, Hossein; Parks, David; Xia, Lirong (2012). "Random Utility Theory for Social Choice". Advances in Neural Information Processing Systems. 25. Curran Associates, Inc. arXiv: 1211.2476 .
  24. ↑ Hemaspaandra, Edith; Spakowski, Holger; Vogel, Jörg (December 2005). "The complexity of Kemeny elections". Theoretical Computer Science. 349 (3): 382–391. doi: 10.1016/j.tcs.2005.08.031 .
  25. ↑ Walker, Joan; Ben-Akiva, Moshe (July 2002). "Generalized random utility model". Mathematical Social Sciences. 43 (3): 303–343. doi:10.1016/S0165-4896(02)00023-9.
  26. ↑ Blavatskyy, Pavlo R. (December 2008). "Stochastic utility theorem" (PDF). Journal of Mathematical Economics. 44 (11): 1049–1056. doi:10.1016/j.jmateco.2007.12.005.
    This page is based on this Wikipedia article
    Text is available under the CC BY-SA 4.0 license; additional terms may apply.
    Images, videos and audio are available under their respective licenses.