
Differential geometry is a mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of differential calculus, integral calculus, linear algebra and multilinear algebra. The field has its origins in the study of spherical geometry as far back as antiquity. It also relates to astronomy, the geodesy of the Earth, and later the study of hyperbolic geometry by Lobachevsky. The simplest examples of smooth spaces are the plane and space curves and surfaces in the three-dimensional Euclidean space, and the study of these shapes formed the basis for development of modern differential geometry during the 18th and 19th centuries.

In the part of mathematics referred to as topology, a surface is a two-dimensional manifold. Some surfaces arise as the boundaries of three-dimensional solids; for example, the sphere is the boundary of the solid ball. Other surfaces arise as graphs of functions of two variables; see the figure at right. However, surfaces can also be defined abstractly, without reference to any ambient space. For example, the Klein bottle is a surface that cannot be embedded in three-dimensional Euclidean space.

In geometry, a catenoid is a type of surface, arising by rotating a catenary curve about an axis. It is a minimal surface, meaning that it occupies the least area when bounded by a closed space. It was formally described in 1744 by the mathematician Leonhard Euler.

In mathematics, a minimal surface is a surface that locally minimizes its area. This is equivalent to having zero mean curvature.
In mathematics, the uniformization theorem says that every simply connected Riemann surface is conformally equivalent to one of three Riemann surfaces: the open unit disk, the complex plane, or the Riemann sphere. The theorem is a generalization of the Riemann mapping theorem from simply connected open subsets of the plane to arbitrary simply connected Riemann surfaces.

A surface of revolution is a surface in Euclidean space created by rotating a curve around an axis of rotation.

The helicoid, also known as helical surface, after the plane and the catenoid, is the third minimal surface to be known.

To hear the shape of a drum is to infer information about the shape of the drumhead from the sound it makes, i.e., from the list of overtones, via the use of mathematical theory.

Richard Melvin Schoen is an American mathematician known for his work in differential geometry and geometric analysis. He is best known for the resolution of the Yamabe problem in 1984.

In mathematics, systolic geometry is the study of systolic invariants of manifolds and polyhedra, as initially conceived by Charles Loewner and developed by Mikhail Gromov, Michael Freedman, Peter Sarnak, Mikhail Katz, Larry Guth, and others, in its arithmetical, ergodic, and topological manifestations. See also a slower-paced Introduction to systolic geometry.

In differential geometry and algebraic geometry, the Enneper surface is a self-intersecting surface that can be described parametrically by:
In mathematics, the Schwarz alternating method or alternating process is an iterative method introduced in 1869–1870 by Hermann Schwarz in the theory of conformal mapping. Given two overlapping regions in the complex plane in each of which the Dirichlet problem could be solved, Schwarz described an iterative method for solving the Dirichlet problem in their union, provided their intersection was suitably well behaved. This was one of several constructive techniques of conformal mapping developed by Schwarz as a contribution to the problem of uniformization, posed by Riemann in the 1850s and first resolved rigorously by Koebe and Poincaré in 1907. It furnished a scheme for uniformizing the union of two regions knowing how to uniformize each of them separately, provided their intersection was topologically a disk or an annulus. From 1870 onwards Carl Neumann also contributed to this theory.

Robert "Bob" Osserman was an American mathematician who worked in geometry. He is specially remembered for his work on the theory of minimal surfaces.
In mathematics a translation surface is a surface obtained from identifying the sides of a polygon in the Euclidean plane by translations. An equivalent definition is a Riemann surface together with a holomorphic 1-form.
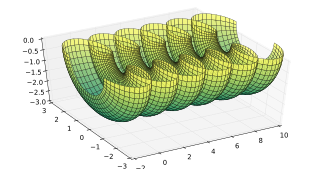
In differential geometry, constant-mean-curvature (CMC) surfaces are surfaces with constant mean curvature. This includes minimal surfaces as a subset, but typically they are treated as special case.
In differential geometry, the Schwarz minimal surfaces are periodic minimal surfaces originally described by Hermann Schwarz.

In differential geometry, the Björling problem is the problem of finding a minimal surface passing through a given curve with prescribed normal. The problem was posed and solved by Swedish mathematician Emanuel Gabriel Björling, with further refinement by Hermann Schwarz.

In differential geometry, a k-noid is a minimal surface with k catenoid openings. In particular, the 3-noid is often called trinoid. The first k-noid minimal surfaces were described by Jorge and Meeks in 1983.
David Allen Hoffman is an American mathematician whose research concerns differential geometry. He is an adjunct professor at Stanford University. In 1985, together with William Meeks, he proved that Costa's surface was embedded. He is a fellow of the American Mathematical Society since 2018, for "contributions to differential geometry, particularly minimal surface theory, and for pioneering the use of computer graphics as an aid to research." He was awarded the Chauvenet Prize in 1990 for his expository article "The Computer-Aided Discovery of New Embedded Minimal Surfaces". He obtained his Ph.D. from Stanford University in 1971 under the supervision of Robert Osserman.














