Related Research Articles
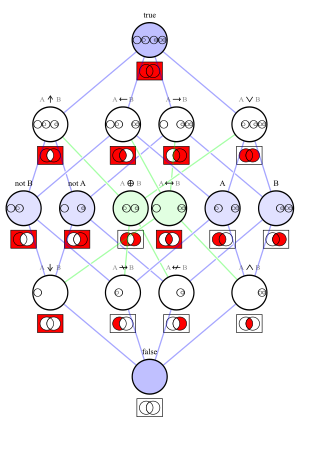
In logic, a logical connective is a logical constant. Connectives can be used to connect logical formulas. For instance in the syntax of propositional logic, the binary connective can be used to join the two atomic formulas and , rendering the complex formula .
Propositional calculus is a branch of logic. It is also called propositional logic, statement logic, sentential calculus, sentential logic, or sometimes zeroth-order logic. It deals with propositions and relations between propositions, including the construction of arguments based on them. Compound propositions are formed by connecting propositions by logical connectives. Propositions that contain no logical connectives are called atomic propositions.
In logic, the semantic principleof bivalence states that every declarative sentence expressing a proposition has exactly one truth value, either true or false. A logic satisfying this principle is called a two-valued logic or bivalent logic.
Classical logic is the intensively studied and most widely used class of deductive logic. Classical logic has had much influence on analytic philosophy.

In logic, negation, also called the logical not or logical complement, is an operation that takes a proposition to another proposition "not ", standing for " is not true", written , or . It is interpreted intuitively as being true when is false, and false when is true. Negation is thus a unary logical connective. It may be applied as an operation on notions, propositions, truth values, or semantic values more generally. In classical logic, negation is normally identified with the truth function that takes truth to falsity. In intuitionistic logic, according to the Brouwer–Heyting–Kolmogorov interpretation, the negation of a proposition is the proposition whose proofs are the refutations of .
In logic and mathematics, a truth value, sometimes called a logical value, is a value indicating the relation of a proposition to truth, which in classical logic has only two possible values.
Intuitionistic logic, sometimes more generally called constructive logic, refers to systems of symbolic logic that differ from the systems used for classical logic by more closely mirroring the notion of constructive proof. In particular, systems of intuitionistic logic do not assume the law of the excluded middle and double negation elimination, which are fundamental inference rules in classical logic.
In logic, false or untrue is the state of possessing negative truth value and is a nullary logical connective. In a truth-functional system of propositional logic, it is one of two postulated truth values, along with its negation, truth. Usual notations of the false are 0, O, and the up tack symbol .
In logic, a three-valued logic is any of several many-valued logic systems in which there are three truth values indicating true, false and some third value. This is contrasted with the more commonly known bivalent logics which provide only for true and false.
Understood in a narrow sense, philosophical logic is the area of logic that studies the application of logical methods to philosophical problems, often in the form of extended logical systems like modal logic. Some theorists conceive philosophical logic in a wider sense as the study of the scope and nature of logic in general. In this sense, philosophical logic can be seen as identical to the philosophy of logic, which includes additional topics like how to define logic or a discussion of the fundamental concepts of logic. The current article treats philosophical logic in the narrow sense, in which it forms one field of inquiry within the philosophy of logic.
In mathematical logic, a propositional variable is an input variable of a truth function. Propositional variables are the basic building-blocks of propositional formulas, used in propositional logic and higher-order logics.
In mathematical logic, a sentence of a predicate logic is a Boolean-valued well-formed formula with no free variables. A sentence can be viewed as expressing a proposition, something that must be true or false. The restriction of having no free variables is needed to make sure that sentences can have concrete, fixed truth values: as the free variables of a (general) formula can range over several values, the truth value of such a formula may vary.
In mathematical logic, a tautology is a formula or assertion that is true in every possible interpretation. An example is "x=y or x≠y". Similarly, "either the ball is green, or the ball is not green" is always true, regardless of the colour of the ball.
Logic is the formal science of using reason and is considered a branch of both philosophy and mathematics and to a lesser extent computer science. Logic investigates and classifies the structure of statements and arguments, both through the study of formal systems of inference and the study of arguments in natural language. The scope of logic can therefore be very large, ranging from core topics such as the study of fallacies and paradoxes, to specialized analyses of reasoning such as probability, correct reasoning, and arguments involving causality. One of the aims of logic is to identify the correct and incorrect inferences. Logicians study the criteria for the evaluation of arguments.
An interpretation is an assignment of meaning to the symbols of a formal language. Many formal languages used in mathematics, logic, and theoretical computer science are defined in solely syntactic terms, and as such do not have any meaning until they are given some interpretation. The general study of interpretations of formal languages is called formal semantics.
Zeroth-order logic is a branch of logic without variables or quantifiers. Some authors use the phrase "zeroth-order logic" as a synonym for propositional calculus, but an alternative definition extends propositional logic by adding constants, operations, and relations on non-Boolean values. Every zeroth-order language in this broader sense is complete and compact.
Philosophy of logic is the area of philosophy that studies the scope and nature of logic. It investigates the philosophical problems raised by logic, such as the presuppositions often implicitly at work in theories of logic and in their application. This involves questions about how logic is to be defined and how different logical systems are connected to each other. It includes the study of the nature of the fundamental concepts used by logic and the relation of logic to other disciplines. According to a common characterization, philosophical logic is the part of the philosophy of logic that studies the application of logical methods to philosophical problems, often in the form of extended logical systems like modal logic. But other theorists draw the distinction between the philosophy of logic and philosophical logic differently or not at all. Metalogic is closely related to the philosophy of logic as the discipline investigating the properties of formal logical systems, like consistency and completeness.
A truth table is a mathematical table used in logic—specifically in connection with Boolean algebra, boolean functions, and propositional calculus—which sets out the functional values of logical expressions on each of their functional arguments, that is, for each combination of values taken by their logical variables. In particular, truth tables can be used to show whether a propositional expression is true for all legitimate input values, that is, logically valid.
In mathematics and mathematical logic, Boolean algebra is a branch of algebra. It differs from elementary algebra in two ways. First, the values of the variables are the truth values true and false, usually denoted 1 and 0, whereas in elementary algebra the values of the variables are numbers. Second, Boolean algebra uses logical operators such as conjunction (and) denoted as ∧, disjunction (or) denoted as ∨, and the negation (not) denoted as ¬. Elementary algebra, on the other hand, uses arithmetic operators such as addition, multiplication, subtraction, and division. Boolean algebra is therefore a formal way of describing logical operations, in the same way that elementary algebra describes numerical operations.
References
- Parigot, Michel (Dec 1997). "Proofs of strong normalisation for second order classical natural deduction". Journal of Symbolic Logic (published 12 March 2014). 62 (4): 1461–1479. doi:10.2307/2275652. ISSN 0022-4812. JSTOR 2275652.