In mathematics, a signed set is a set of elements together with an assignment of a sign (positive or negative) to each element of the set.
Signed sets may be represented mathematically as an ordered pair of disjoint sets, one set for their positive elements and another for their negative elements. [1] Alternatively, they may be represented as a Boolean function, a function whose domain is the underlying unsigned set (possibly specified explicitly as a separate part of the representation) and whose range is a two-element set representing the signs. [2] [3]
Signed sets may also be called -graded sets. [2]
Signed sets are fundamental to the definition of oriented matroids. [1]
They may also be used to define the faces of a hypercube. If the hypercube consists of all points in Euclidean space of a given dimension whose Cartesian coordinates are in the interval , then a signed subset of the coordinate axes can be used to specify the points whose coordinates within the subset are or (according to the sign in the signed subset) and whose other coordinates may be anywhere in the interval . This subset of points forms a face, whose codimension is the cardinality of the signed subset. [4]
The number of signed subsets of a given finite set of elements is , a power of three, because there are three choices for each element: it may be absent from the subset, present with positive sign, or present with negative sign. [5] For the same reason, the number of signed subsets of cardinality is
and summing these gives an instance of the binomial theorem,
An analogue of the Erdős–Ko–Rado theorem on intersecting families of sets holds also for signed sets. The intersection of two signed sets is defined to be the signed set of elements that belong to both and have the same sign in both. According to this theorem, for any a collection of signed subsets of an -element set, all having cardinality and all pairs having a non-empty intersection, the number of signed subsets in the collection is at most
For instance, an intersecting family of this size can be obtained by choosing the sign of a single fixed element, and taking the family to be all signed subsets of cardinality that contain this element with this sign. For this theorem follows immediately from the unsigned Erdős–Ko–Rado theorem, as the unsigned versions of the subsets form an intersecting family and each unsigned set can correspond to at most signed sets. However, for larger values of a different proof is needed. [3]
In combinatorics, a branch of mathematics, a matroid is a structure that abstracts and generalizes the notion of linear independence in vector spaces. There are many equivalent ways to define a matroid axiomatically, the most significant being in terms of: independent sets; bases or circuits; rank functions; closure operators; and closed sets or flats. In the language of partially ordered sets, a finite matroid is equivalent to a geometric lattice.
In abstract algebra, a subset of a field is algebraically independent over a subfield if the elements of do not satisfy any non-trivial polynomial equation with coefficients in .
In combinatorics, the Erdős–Ko–Rado theorem of Paul Erdős, Chao Ko, and Richard Rado is a theorem on intersecting set families.
Sperner's theorem, in discrete mathematics, describes the largest possible families of finite sets none of which contain any other sets in the family. It is one of the central results in extremal set theory. It is named after Emanuel Sperner, who published it in 1928.
In geometry and combinatorics, an arrangement of hyperplanes is an arrangement of a finite set A of hyperplanes in a linear, affine, or projective space S. Questions about a hyperplane arrangement A generally concern geometrical, topological, or other properties of the complement, M(A), which is the set that remains when the hyperplanes are removed from the whole space. One may ask how these properties are related to the arrangement and its intersection semilattice. The intersection semilattice of A, written L(A), is the set of all subspaces that are obtained by intersecting some of the hyperplanes; among these subspaces are S itself, all the individual hyperplanes, all intersections of pairs of hyperplanes, etc.. These intersection subspaces of A are also called the flats ofA. The intersection semilattice L(A) is partially ordered by reverse inclusion.
In algebraic combinatorics, the Kruskal–Katona theorem gives a complete characterization of the f-vectors of abstract simplicial complexes. It includes as a special case the Erdős–Ko–Rado theorem and can be restated in terms of uniform hypergraphs. It is named after Joseph Kruskal and Gyula O. H. Katona, but has been independently discovered by several others.
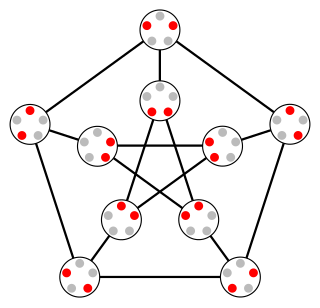
In graph theory, the Kneser graphK(n, k) is the graph whose vertices correspond to the k-element subsets of a set of n elements, and where two vertices are adjacent if and only if the two corresponding sets are disjoint. Kneser graphs are named after Martin Kneser, who first investigated them in 1955.
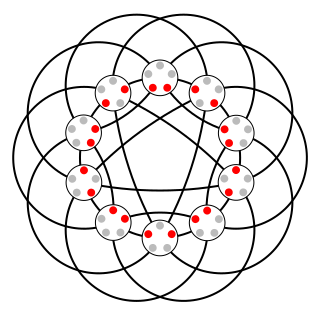
Johnson graphs are a special class of undirected graphs defined from systems of sets. The vertices of the Johnson graph are the -element subsets of an -element set; two vertices are adjacent when the intersection of the two vertices (subsets) contains -elements. Both Johnson graphs and the closely related Johnson scheme are named after Selmer M. Johnson.
In graph theory, the hypercube graphQn is the graph formed from the vertices and edges of an n-dimensional hypercube. For instance, the cubical graph Q3 is the graph formed by the 8 vertices and 12 edges of a three-dimensional cube. Qn has 2n vertices, 2n−1n edges, and is a regular graph with n edges touching each vertex.
Kuratowski's free set theorem, named after Kazimierz Kuratowski, is a result of set theory, an area of mathematics. It is a result which has been largely forgotten for almost 50 years, but has been applied recently in solving several lattice theory problems, such as the congruence lattice problem.
In mathematics, infinitary combinatorics, or combinatorial set theory, is an extension of ideas in combinatorics to infinite sets. Some of the things studied include continuous graphs and trees, extensions of Ramsey's theorem, and Martin's axiom. Recent developments concern combinatorics of the continuum and combinatorics on successors of singular cardinals.
In graph theory, the De Bruijn–Erdős theorem relates graph coloring of an infinite graph to the same problem on its finite subgraphs. It states that, when all finite subgraphs can be colored with colors, the same is true for the whole graph. The theorem was proved by Nicolaas Govert de Bruijn and Paul Erdős (1951), after whom it is named.
In partition calculus, part of combinatorial set theory, a branch of mathematics, the Erdős–Rado theorem is a basic result extending Ramsey's theorem to uncountable sets. It is named after Paul Erdős and Richard Rado. It is sometimes also attributed to Đuro Kurepa who proved it under the additional assumption of the generalised continuum hypothesis, and hence the result is sometimes also referred to as the Erdős–Rado–Kurepa theorem.
In the mathematical theory of infinite graphs, the Erdős–Dushnik–Miller theorem is a form of Ramsey's theorem stating that every infinite graph contains either a countably infinite independent set, or a clique with the same cardinality as the whole graph.
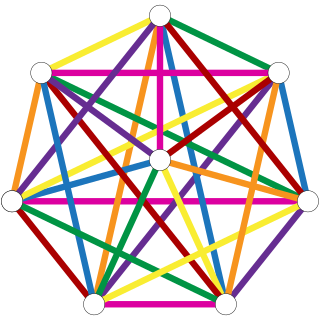
In combinatorial mathematics, Baranyai's theorem deals with the decompositions of complete hypergraphs.
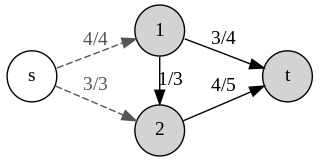
An oriented matroid is a mathematical structure that abstracts the properties of directed graphs, vector arrangements over ordered fields, and hyperplane arrangements over ordered fields. In comparison, an ordinary matroid abstracts the dependence properties that are common both to graphs, which are not necessarily directed, and to arrangements of vectors over fields, which are not necessarily ordered.
In matroid theory, a field within mathematics, a gammoid is a certain kind of matroid, describing sets of vertices that can be reached by vertex-disjoint paths in a directed graph.
In combinatorial mathematics, a partial permutation, or sequence without repetition, on a finite set S is a bijection between two specified subsets of S. That is, it is defined by two subsets U and V of equal size, and a one-to-one mapping from U to V. Equivalently, it is a partial function on S that can be extended to a permutation.
In mathematics and computer science, a matroid oracle is a subroutine through which an algorithm may access a matroid, an abstract combinatorial structure that can be used to describe the linear dependencies between vectors in a vector space or the spanning trees of a graph, among other applications.
In the mathematical theory of matroids, a matroid representation is a family of vectors whose linear independence relation is the same as that of a given matroid. Matroid representations are analogous to group representations; both types of representation provide abstract algebraic structures with concrete descriptions in terms of linear algebra.
