Snark (graph theory)

Last updated May 10, 2023

In the mathematical field of graph theory, a snark is an undirected graph with exactly three edges per vertex whose edges cannot be colored with only three colors. In order to avoid trivial cases, snarks are often restricted to have additional requirements on their connectivity and on the length of their cycles. Infinitely many snarks exist.

One of the equivalent forms of the four color theorem is that every snark is a non-planar graph. Research on snarks originated in Peter G. Tait's work on the four color theorem in 1880, but their name is much newer, given to them by Martin Gardner in 1976. Beyond coloring, snarks also have connections to other hard problems in graph theory: writing in the Electronic Journal of Combinatorics , Miroslav Chladný and Martin Škoviera state that

In the study of various important and difficult problems in graph theory (such as the cycle double cover conjecture and the 5-flow conjecture), one encounters an interesting but somewhat mysterious variety of graphs called snarks. In spite of their simple definition...and over a century long investigation, their properties and structure are largely unknown.^[1]

As well as the problems they mention, W. T. Tutte's snark conjecture concerns the existence of Petersen graphs as graph minors of snarks; its proof has been long announced but remains unpublished, and would settle a special case of the existence of nowhere zero 4-flows.

History and examples

Snarks were so named by the American mathematician Martin Gardner in 1976, after the mysterious and elusive object of the poem The Hunting of the Snark by Lewis Carroll.^[2] However, the study of this class of graphs is significantly older than their name. Peter G. Tait initiated the study of snarks in 1880, when he proved that the four color theorem is equivalent to the statement that no snark is planar.^[3] The first graph known to be a snark was the Petersen graph; it was proved to be a snark by Julius Petersen in 1898,^[4] although it had already been studied for a different purpose by Alfred Kempe in 1886.^[5]

The next four known snarks were

the Blanuša snarks (two with 18 vertices), discovered by Danilo Blanuša in 1946,^[6]
the Descartes snark (210 vertices), discovered by Bill Tutte in 1948,^[7] and
the Szekeres snark (50 vertices), discovered by George Szekeres in 1973.^[8]

In 1975, Rufus Isaacs generalized Blanuša's method to construct two infinite families of snarks: the flower snarks and the Blanuša–Descartes–Szekeres snarks, a family that includes the two Blanuša snarks, the Descartes snark and the Szekeres snark. Isaacs also discovered a 30-vertex snark that does not belong to the Blanuša–Descartes–Szekeres family and that is not a flower snark: the double-star snark.^[9] The 50-vertex Watkins snark was discovered in 1989.^[10]

Another notable cubic non-three-edge-colorable graph is Tietze's graph, with 12 vertices; as Heinrich Franz Friedrich Tietze discovered in 1910, it forms the boundary of a subdivision of the Möbius strip requiring six colors.^[11] However, because it contains a triangle, it is not generally considered a snark. Under strict definitions of snarks, the smallest snarks are the Petersen graph and Blanuša snarks, followed by six different 20-vertex snarks.^[12]

A list of all of the snarks up to 36 vertices (according to a strict definition), and up to 34 vertices (under a weaker definition), was generated by Gunnar Brinkmann, Jan Goedgebeur, Jonas Hägglund and Klas Markström in 2012.^[12] The number of snarks for a given even number of vertices grows at least exponentially in the number of vertices.^[13] (Because they have odd-degree vertices, all snarks must have an even number of vertices by the handshaking lemma.)^[14] OEIS sequence A130315 contains the number of non-trivial snarks of $2n$ vertices for small values of $n$ .^[15]

Definition

The precise definition of snarks varies among authors,^[12]^[9] but generally refers to cubic graphs (having exactly three edges at each vertex) whose edges cannot be colored with only three colors. By Vizing's theorem, the number of colors needed for the edges of a cubic graph is either three ("class one" graphs) or four ("class two" graphs), so snarks are cubic graphs of class two. However, in order to avoid cases where a snark is of class two for trivial reasons, or is constructed in a trivial way from smaller graphs, additional restrictions on connectivity and cycle lengths are often imposed. In particular:

If a cubic graph has a bridge, an edge whose removal would disconnect it, then it cannot be of class one. By the handshaking lemma, the subgraphs on either side of the bridge have an odd number of vertices each. Whichever of three colors is chosen for the bridge, their odd number of vertices prevents these subgraphs from being covered by cycles that alternate between the other two colors, as would be necessary in a 3-edge-coloring. For this reason, snarks are generally required to be bridgeless.^[2]^[9]
A loop (an edge connecting a vertex to itself) cannot be colored without causing the same color to appear twice at that vertex, a violation of the usual requirements for graph edge coloring. Additionally, a cycle consisting of two vertices connected by two edges can always be replaced by a single edge connecting their two other neighbors, simplifying the graph without changing its three-edge-colorability. For these reasons, snarks are generally restricted to simple graphs, graphs without loops or multiple adjacencies.^[9]
If a graph contains a triangle, then it can again be simplified without changing its three-edge-colorability, by contracting the three vertices of the triangle into a single vertex. Therefore, many definitions of snarks forbid triangles.^[9] However, although this requirement was also stated in Gardner's work giving the name "snark" to these graphs, Gardner lists Tietze's graph, which contains a triangle, as being a snark.^[2]
If a graph contains a four-vertex cycle, it can be simplified in two different ways by removing two opposite edges of the cycle and replacing the resulting paths of degree-two vertices by single edges. It has a three-edge-coloring if and only if at least one of these simplifications does. Therefore, Isaacs requires a "nontrivial" cubic class-two graph to avoid four-vertex cycles,^[9] and other authors have followed suit in forbidding these cycles.^[12] The requirement that a snark avoid cycles of length four or less can be summarized by stating that the girth of these graphs, the length of their shortest cycles, is at least five.
More strongly, the definition used by Brinkmann et al. (2012) requires snarks to be cyclically 4-edge-connected. That means there can be no subset of three or fewer edges, the removal of which would disconnect the graph into two subgraphs each of which has at least one cycle. Brinkmann et al. define a snark to be a cubic and cyclically 4-edge-connected graph of girth five or more and class two; they define a "weak snark" to allow girth four.^[12]

Although these definitions only consider constraints on the girth up to five, snarks with arbitrarily large girth exist.^[16]

Properties

Work by Peter G. Tait established that the four-color theorem is true if and only if every snark is non-planar.^[3] This theorem states that every planar graph has a graph coloring of its the vertices with four colors, but Tait showed how to convert 4-vertex-colorings of maximal planar graphs into 3-edge-colorings of their dual graphs, which are cubic and planar, and vice versa. A planar snark would therefore necessarily be dual to a counterexample to the four-color theorem. Thus, the subsequent proof of the four-color theorem ^[17] also demonstrates that all snarks are non-planar.^[18]

All snarks are non-Hamiltonian: when a cubic graph has a Hamiltonian cycle, it is always possible to 3-color its edges, by using two colors in alternation for the cycle, and the third color for the remaining edges. However, many known snarks are close to being Hamiltonian, in the sense that they are hypohamiltonian graphs: the removal of any single vertex leaves a Hamiltonian subgraph. A hypohamiltonian snark must be bicritical: the removal of any two vertices leaves a three-edge-colorable subgraph.^[19] The oddness of a cubic graph is defined as the minimum number of odd cycles, in any system of cycles that covers each vertex once (a 2-factor). For the same reason that they have no Hamiltonian cycles, snarks have positive oddness: a completely even 2-factor would lead to a 3-edge-coloring, and vice versa. It is possible to construct infinite families of snarks whose oddness grows linearly with their numbers of vertices.^[14]

The cycle double cover conjecture posits that in every bridgeless graph one can find a collection of cycles covering each edge twice, or equivalently that the graph can be embedded onto a surface in such a way that all faces of the embedding are simple cycles. When a cubic graph has a 3-edge-coloring, it has a cycle double cover consisting of the cycles formed by each pair of colors. Therefore, among cubic graphs, the snarks are the only possible counterexamples. More generally, snarks form the difficult case for this conjecture: if it is true for snarks, it is true for all graphs.^[20] In this connection, Branko Grünbaum conjectured that no snark could be embedded onto a surface in such a way that all faces are simple cycles and such that every two faces either are disjoint or share only a single edge; if any snark had such an embedding, its faces would form a cycle double cover. However, a counterexample to Grünbaum's conjecture was found by Martin Kochol.^[21]

Determining whether a given cyclically 5-connected cubic graph is 3-edge-colorable is NP-complete. Therefore, determining whether a graph is a snark is co-NP-complete.^[22]

Snark conjecture

W. T. Tutte conjectured that every snark has the Petersen graph as a minor. That is, he conjectured that the smallest snark, the Petersen graph, may be formed from any other snark by contracting some edges and deleting others. Equivalently (because the Petersen graph has maximum degree three) every snark has a subgraph that can be formed from the Petersen graph by subdividing some of its edges. This conjecture is a strengthened form of the four color theorem, because any graph containing the Petersen graph as a minor must be nonplanar. In 1999, Neil Robertson, Daniel P. Sanders, Paul Seymour, and Robin Thomas announced a proof of this conjecture.^[23] Steps towards this result have been published,^[24]^[25] but as of 2022^[update], the complete proof remains unpublished.^[18]^[24] See the Hadwiger conjecture for other problems and results relating graph coloring to graph minors.

Tutte also conjectured a generalization to arbitrary graphs: every bridgeless graph with no Petersen minor has a nowhere zero 4-flow. That is, the edges of the graph may be assigned a direction, and a number from the set {1, 2, 3}, such that the sum of the incoming numbers minus the sum of the outgoing numbers at each vertex is divisible by four. As Tutte showed, for cubic graphs such an assignment exists if and only if the edges can be colored by three colors, so the conjecture would follow from the snark conjecture in this case. However, proving the snark conjecture would not settle the question of the existence of 4-flows for non-cubic graphs.^[26]

Related Research Articles

In mathematics, the four color theorem, or the four color map theorem, states that no more than four colors are required to color the regions of any map so that no two adjacent regions have the same color. Adjacent means that two regions share a common boundary curve segment, not merely a corner where three or more regions meet. It was the first major theorem to be proved using a computer. Initially, this proof was not accepted by all mathematicians because the computer-assisted proof was infeasible for a human to check by hand. The proof has gained wide acceptance since then, although some doubters remain.

In mathematics, Tait's conjecture states that "Every 3-connected planar cubic graph has a Hamiltonian cycle through all its vertices". It was proposed by P. G. Tait (1884) and disproved by W. T. Tutte (1946), who constructed a counterexample with 25 faces, 69 edges and 46 vertices. Several smaller counterexamples, with 21 faces, 57 edges and 38 vertices, were later proved minimal by Holton & McKay (1988). The condition that the graph be 3-regular is necessary due to polyhedra such as the rhombic dodecahedron, which forms a bipartite graph with six degree-four vertices on one side and eight degree-three vertices on the other side; because any Hamiltonian cycle would have to alternate between the two sides of the bipartition, but they have unequal numbers of vertices, the rhombic dodecahedron is not Hamiltonian.

In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named after Julius Petersen, who in 1898 constructed it to be the smallest bridgeless cubic graph with no three-edge-coloring.

This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

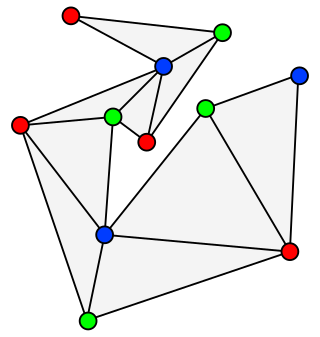
In graph theory, an outerplanar graph is a graph that has a planar drawing for which all vertices belong to the outer face of the drawing.

In graph theory, an undirected graph $H$ is called a minor of the graph $G$ if $H$ can be formed from $G$ by deleting edges, vertices and by contracting edges.

In graph theory, a uniquely colorable graph is a $k$ -chromatic graph that has only one possible (proper) $k$ -coloring up to permutation of the colors. Equivalently, there is only one way to partition its vertices into $k$ independent sets and there is no way to partition them into $k - 1$ independent sets.

In graph theory, an edge coloring of a graph is an assignment of "colors" to the edges of the graph so that no two incident edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several different types of graph coloring. The edge-coloring problem asks whether it is possible to color the edges of a given graph using at most $k$ different colors, for a given value of $k$ , or with the fewest possible colors. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph. For example, the edges of the graph in the illustration can be colored by three colors but cannot be colored by two colors, so the graph shown has chromatic index three.

In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words, a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs.

In graph theory, the Hadwiger conjecture states that if $is loopless and has no minor then its chromatic number satisfies . It is known to be true for . The conjecture is a generalization of the four-color theorem and is considered to be one of the most important and challenging open problems in the field.$

In graph theory, Vizing's theorem states that every simple undirected graph may be edge colored using a number of colors that is at most one larger than the maximum degree $Δ$ of the graph. At least $Δ$ colors are always necessary, so the undirected graphs may be partitioned into two classes: "class one" graphs for which $Δ$ colors suffice, and "class two" graphs for which $Δ + 1$ colors are necessary. A more general version of Vizing's theorem states that every undirected multigraph without loops can be colored with at most $Δ+µ$ colors, where $µ$ is the multiplicity of the multigraph. The theorem is named for Vadim G. Vizing who published it in 1964.

<span class="mw-page-title-main">Hypercube graph</span> Graphs formed by a hypercubes edges and vertices

In graph theory, the hypercube graph $Q n$ is the graph formed from the vertices and edges of an $n$ -dimensional hypercube. For instance, the cube graph $Q 3$ is the graph formed by the 8 vertices and 12 edges of a three-dimensional cube. $Q n$ has $2 n$ vertices, $2 n - 1 n$ edges, and is a regular graph with $n$ edges touching each vertex.

<span class="mw-page-title-main">Grötzsch graph</span> Triangle-free graph requiring four colors

In the mathematical field of graph theory, the Grötzsch graph is a triangle-free graph with 11 vertices, 20 edges, chromatic number 4, and crossing number 5. It is named after German mathematician Herbert Grötzsch, who used it as an example in connection with his 1959 theorem that planar triangle-free graphs are 3-colorable.

In graph theory, a nowhere-zero flow or NZ flow is a network flow that is nowhere zero. It is intimately connected to coloring planar graphs.

In the mathematical field of graph theory, a graph G is said to be hypohamiltonian if G itself does not have a Hamiltonian cycle but every graph formed by removing a single vertex from G is Hamiltonian.

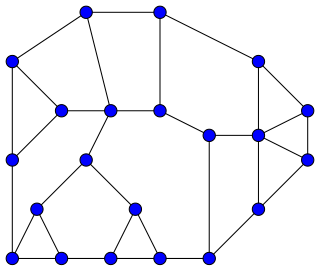
In graph theory, a Halin graph is a type of planar graph, constructed by connecting the leaves of a tree into a cycle. The tree must have at least four vertices, none of which has exactly two neighbors; it should be drawn in the plane so none of its edges cross, and the cycle connects the leaves in their clockwise ordering in this embedding. Thus, the cycle forms the outer face of the Halin graph, with the tree inside it.

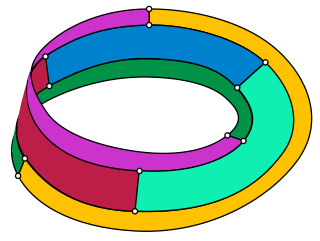
<span class="mw-page-title-main">Tietze's graph</span> Undirected cubic graph with 12 vertices and 18 edges

In the mathematical field of graph theory, Tietze's graph is an undirected cubic graph with 12 vertices and 18 edges. It is named after Heinrich Franz Friedrich Tietze, who showed in 1910 that the Möbius strip can be subdivided into six regions that all touch each other – three along the boundary of the strip and three along its center line – and therefore that graphs that are embedded onto the Möbius strip may require six colors. The boundary segments of the regions of Tietze's subdivision form an embedding of Tietze's graph.

In graph-theoretic mathematics, a cycle double cover is a collection of cycles in an undirected graph that together include each edge of the graph exactly twice. For instance, for any polyhedral graph, the faces of a convex polyhedron that represents the graph provide a double cover of the graph: each edge belongs to exactly two faces.

Barnette's conjecture is an unsolved problem in graph theory, a branch of mathematics, concerning Hamiltonian cycles in graphs. It is named after David W. Barnette, a professor emeritus at the University of California, Davis; it states that every bipartite polyhedral graph with three edges per vertex has a Hamiltonian cycle.

The Petersen Graph is a mathematics book about the Petersen graph and its applications in graph theory. It was written by Derek Holton and John Sheehan, and published in 1993 by the Cambridge University Press as volume 7 in their Australian Mathematical Society Lecture Series.

References

↑ Chladný, Miroslav; Škoviera, Martin (2010), "Factorisation of snarks", Electronic Journal of Combinatorics , 17: R32, doi: 10.37236/304 , MR 2595492
1 2 3 Gardner, Martin (1976), "Snarks, boojums, and other conjectures related to the four-color-map theorem", Mathematical Games, Scientific American, 4 (234): 126–130, Bibcode:1976SciAm.234d.126G, doi:10.1038/scientificamerican0476-126, JSTOR 24950334
1 2 Tait, Peter Guthrie (1880), "Remarks on the colourings of maps", Proceedings of the Royal Society of Edinburgh, 10: 729, doi:10.1017/S0370164600044643
↑ Petersen, Julius (1898), "Sur le théorème de Tait", L'Intermédiaire des Mathématiciens , 5: 225–227
↑ Kempe, A. B. (1886), "A memoir on the theory of mathematical form", Philosophical Transactions of the Royal Society of London, 177: 1–70, doi:10.1098/rstl.1886.0002, S2CID 108716533
↑ Blanuša, Danilo (1946), "Le problème des quatre couleurs", Glasnik Matematičko-Fizički i Astronomski, Ser. II, 1: 31–42, MR 0026310
↑ Descartes, Blanche (1948), "Network-colourings", The Mathematical Gazette , 32 (299): 67–69, doi:10.2307/3610702, JSTOR 3610702, MR 0026309, S2CID 250434686
↑ Szekeres, George (1973), "Polyhedral decompositions of cubic graphs", Bulletin of the Australian Mathematical Society, 8 (3): 367–387, doi: 10.1017/S0004972700042660
1 2 3 4 5 6 Isaacs, Rufus (1975), "Infinite families of non-trivial trivalent graphs which are not Tait-colorable", The American Mathematical Monthly , 82 (3): 221–239, doi:10.2307/2319844, JSTOR 2319844
↑ Watkins, John J. (1989), "Snarks", in Capobianco, Michael F.; Guan, Mei Gu; Hsu, D. Frank; Tian, Feng (eds.), Graph theory and its Applications: East and West, Proceedings of the First China–USA International Conference held in Jinan, June 9–20, 1986, Annals of the New York Academy of Sciences, vol. 576, New York: New York Academy of Sciences, pp. 606–622, doi:10.1111/j.1749-6632.1989.tb16441.x, MR 1110857, S2CID 222072657
↑ Tietze, Heinrich (1910), "Einige Bemerkungen zum Problem des Kartenfärbens auf einseitigen Flächen" [Some remarks on the problem of map coloring on one-sided surfaces](PDF), DMV Annual Report, 19: 155–159
1 2 3 4 5 Brinkmann, Gunnar; Goedgebeur, Jan; Hägglund, Jonas; Markström, Klas (2012), "Generation and properties of snarks", Journal of Combinatorial Theory, Series B , 103 (4): 468–488, arXiv: 1206.6690 , doi:10.1016/j.jctb.2013.05.001, MR 3071376, S2CID 15284747
↑ Skupień, Zdzisław (2007), "Exponentially many hypohamiltonian snarks", 6th Czech-Slovak International Symposium on Combinatorics, Graph Theory, Algorithms and Applications, Electronic Notes in Discrete Mathematics, vol. 28, pp. 417–424, doi:10.1016/j.endm.2007.01.059
1 2 Lukot'ka, Robert; Máčajová, Edita; Mazák, Ján; Škoviera, Martin (2015), "Small snarks with large oddness", Electronic Journal of Combinatorics , 22 (1), Paper 1.51, arXiv: 1212.3641 , doi:10.37236/3969, MR 3336565, S2CID 4805178
↑ Sloane, N. J. A. (ed.), "SequenceA130315", The On-Line Encyclopedia of Integer Sequences , OEIS Foundation
↑ Kochol, Martin (1996), "Snarks without small cycles", Journal of Combinatorial Theory, Series B , 67 (1): 34–47, doi: 10.1006/jctb.1996.0032 , MR 1385382
↑ Appel, Kenneth; Haken, Wolfgang (1989), Every Planar Map is Four-Colorable, Contemporary Mathematics, vol. 98, With the collaboration of J. Koch., Providence, RI: American Mathematical Society, doi:10.1090/conm/098, ISBN 0-8218-5103-9, MR 1025335, S2CID 8735627
1 2 belcastro, sarah-marie (2012), "The continuing saga of snarks", The College Mathematics Journal , 43 (1): 82–87, doi:10.4169/college.math.j.43.1.082, MR 2875562, S2CID 118189042
↑ Steffen, E. (1998), "Classification and characterizations of snarks", Discrete Mathematics , 188 (1–3): 183–203, doi: 10.1016/S0012-365X(97)00255-0 , MR 1630478 ; Steffen, E. (2001), "On bicritical snarks", Math. Slovaca, 51 (2): 141–150, MR 1841443
↑ Jaeger, François (1985), "A survey of the cycle double cover conjecture", in Alspach, B. R.; Godsil, C. D. (eds.), Annals of Discrete Mathematics 27: Cycles in Graphs, North-Holland Mathematics Studies, vol. 27, pp. 1–12, doi:10.1016/S0304-0208(08)72993-1, ISBN 978-0-444-87803-8
↑ Kochol, Martin (2009), "Polyhedral embeddings of snarks in orientable surfaces", Proceedings of the American Mathematical Society , vol. 137, pp. 1613–1619
↑ Kochol, Martin (2010), "Complexity of 3-edge-coloring in the class of cubic graphs with a polyhedral embedding in an orientable surface", Discrete Applied Mathematics, 158 (16): 1856–1860, doi: 10.1016/j.dam.2010.06.019 , MR 2679785
↑ Thomas, Robin (1999), "Recent excluded minor theorems for graphs" (PDF), Surveys in Combinatorics, 1999, Cambridge University Press, pp. 201–222
1 2 Edwards, Katherine; Sanders, Daniel P.; Seymour, Paul; Thomas, Robin (2016), "Three-edge-colouring doublecross cubic graphs" (PDF), Journal of Combinatorial Theory, Series B , 119: 66–95, doi:10.1016/j.jctb.2015.12.006, MR 3486338, S2CID 2656843
↑ Robertson, Neil; Seymour, Paul; Thomas, Robin (2019), "Excluded minors in cubic graphs", Journal of Combinatorial Theory, Series B , 138: 219–285, arXiv: 1403.2118 , doi:10.1016/j.jctb.2019.02.002, MR 3979232, S2CID 16237685
↑ DeVos, Matthew (March 7, 2007), "4-flow conjecture", Open Problem Garden

External links

Weisstein, Eric W., "Snark", MathWorld

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[chladny2010-1] Chladný, Miroslav; Škoviera, Martin (2010), "Factorisation of snarks", Electronic Journal of Combinatorics , 17: R32, doi: 10.37236/304 , MR 2595492

[gardner-2] 1 2 3 Gardner, Martin (1976), "Snarks, boojums, and other conjectures related to the four-color-map theorem", Mathematical Games, Scientific American, 4 (234): 126–130, Bibcode:1976SciAm.234d.126G, doi:10.1038/scientificamerican0476-126, JSTOR 24950334

[tait-3] 1 2 Tait, Peter Guthrie (1880), "Remarks on the colourings of maps", Proceedings of the Royal Society of Edinburgh, 10: 729, doi:10.1017/S0370164600044643

[petersen-4] Petersen, Julius (1898), "Sur le théorème de Tait", L'Intermédiaire des Mathématiciens , 5: 225–227

[kempe-5] Kempe, A. B. (1886), "A memoir on the theory of mathematical form", Philosophical Transactions of the Royal Society of London, 177: 1–70, doi:10.1098/rstl.1886.0002, S2CID 108716533

[blanusa-6] Blanuša, Danilo (1946), "Le problème des quatre couleurs", Glasnik Matematičko-Fizički i Astronomski, Ser. II, 1: 31–42, MR 0026310

[descartes-7] Descartes, Blanche (1948), "Network-colourings", The Mathematical Gazette , 32 (299): 67–69, doi:10.2307/3610702, JSTOR 3610702, MR 0026309, S2CID 250434686

[szekeres-8] Szekeres, George (1973), "Polyhedral decompositions of cubic graphs", Bulletin of the Australian Mathematical Society, 8 (3): 367–387, doi: 10.1017/S0004972700042660

[isaacs-9] 1 2 3 4 5 6 Isaacs, Rufus (1975), "Infinite families of non-trivial trivalent graphs which are not Tait-colorable", The American Mathematical Monthly , 82 (3): 221–239, doi:10.2307/2319844, JSTOR 2319844

[watkins-10] Watkins, John J. (1989), "Snarks", in Capobianco, Michael F.; Guan, Mei Gu; Hsu, D. Frank; Tian, Feng (eds.), Graph theory and its Applications: East and West, Proceedings of the First China–USA International Conference held in Jinan, June 9–20, 1986, Annals of the New York Academy of Sciences, vol. 576, New York: New York Academy of Sciences, pp. 606–622, doi:10.1111/j.1749-6632.1989.tb16441.x, MR 1110857, S2CID 222072657

[tietze-11] Tietze, Heinrich (1910), "Einige Bemerkungen zum Problem des Kartenfärbens auf einseitigen Flächen" [Some remarks on the problem of map coloring on one-sided surfaces](PDF), DMV Annual Report, 19: 155–159

[bghm-12] 1 2 3 4 5 Brinkmann, Gunnar; Goedgebeur, Jan; Hägglund, Jonas; Markström, Klas (2012), "Generation and properties of snarks", Journal of Combinatorial Theory, Series B , 103 (4): 468–488, arXiv: 1206.6690 , doi:10.1016/j.jctb.2013.05.001, MR 3071376, S2CID 15284747

[skupien-13] Skupień, Zdzisław (2007), "Exponentially many hypohamiltonian snarks", 6th Czech-Slovak International Symposium on Combinatorics, Graph Theory, Algorithms and Applications, Electronic Notes in Discrete Mathematics, vol. 28, pp. 417–424, doi:10.1016/j.endm.2007.01.059

[oddness-14] 1 2 Lukot'ka, Robert; Máčajová, Edita; Mazák, Ján; Škoviera, Martin (2015), "Small snarks with large oddness", Electronic Journal of Combinatorics , 22 (1), Paper 1.51, arXiv: 1212.3641 , doi:10.37236/3969, MR 3336565, S2CID 4805178

[15] Sloane, N. J. A. (ed.), "SequenceA130315", The On-Line Encyclopedia of Integer Sequences , OEIS Foundation

[kochol1996-16] Kochol, Martin (1996), "Snarks without small cycles", Journal of Combinatorial Theory, Series B , 67 (1): 34–47, doi: 10.1006/jctb.1996.0032 , MR 1385382

[4color-17] Appel, Kenneth; Haken, Wolfgang (1989), Every Planar Map is Four-Colorable, Contemporary Mathematics, vol. 98, With the collaboration of J. Koch., Providence, RI: American Mathematical Society, doi:10.1090/conm/098, ISBN 0-8218-5103-9, MR 1025335, S2CID 8735627

[belcastro-18] 1 2 belcastro, sarah-marie (2012), "The continuing saga of snarks", The College Mathematics Journal , 43 (1): 82–87, doi:10.4169/college.math.j.43.1.082, MR 2875562, S2CID 118189042

[steffen-19] Steffen, E. (1998), "Classification and characterizations of snarks", Discrete Mathematics , 188 (1–3): 183–203, doi: 10.1016/S0012-365X(97)00255-0 , MR 1630478 ; Steffen, E. (2001), "On bicritical snarks", Math. Slovaca, 51 (2): 141–150, MR 1841443

[jaeger-20] Jaeger, François (1985), "A survey of the cycle double cover conjecture", in Alspach, B. R.; Godsil, C. D. (eds.), Annals of Discrete Mathematics 27: Cycles in Graphs, North-Holland Mathematics Studies, vol. 27, pp. 1–12, doi:10.1016/S0304-0208(08)72993-1, ISBN 978-0-444-87803-8

[kochol2009-21] Kochol, Martin (2009), "Polyhedral embeddings of snarks in orientable surfaces", Proceedings of the American Mathematical Society , vol. 137, pp. 1613–1619

[kochol2010-22] Kochol, Martin (2010), "Complexity of 3-edge-coloring in the class of cubic graphs with a polyhedral embedding in an orientable surface", Discrete Applied Mathematics, 158 (16): 1856–1860, doi: 10.1016/j.dam.2010.06.019 , MR 2679785

[thomas-23] Thomas, Robin (1999), "Recent excluded minor theorems for graphs" (PDF), Surveys in Combinatorics, 1999, Cambridge University Press, pp. 201–222

[doublecross-24] 1 2 Edwards, Katherine; Sanders, Daniel P.; Seymour, Paul; Thomas, Robin (2016), "Three-edge-colouring doublecross cubic graphs" (PDF), Journal of Combinatorial Theory, Series B , 119: 66–95, doi:10.1016/j.jctb.2015.12.006, MR 3486338, S2CID 2656843

[rst2019-25] Robertson, Neil; Seymour, Paul; Thomas, Robin (2019), "Excluded minors in cubic graphs", Journal of Combinatorial Theory, Series B , 138: 219–285, arXiv: 1403.2118 , doi:10.1016/j.jctb.2019.02.002, MR 3979232, S2CID 16237685

[garden-26] DeVos, Matthew (March 7, 2007), "4-flow conjecture", Open Problem Garden

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]