
In celestial mechanics, escape velocity or escape speed is the minimum speed needed for a free, non-propelled object to escape from the gravitational influence of a primary body, thus reaching an infinite distance from it. It is typically stated as an ideal speed, ignoring atmospheric friction. Although the term "escape velocity" is common, it is more accurately described as a speed than a velocity because it is independent of direction; the escape speed increases with the mass of the primary body and decreases with the distance from the primary body. The escape speed thus depends on how far the object has already traveled, and its calculation at a given distance takes into account that without new acceleration it will slow down as it travels—due to the massive body's gravity—but it will never quite slow to a stop.
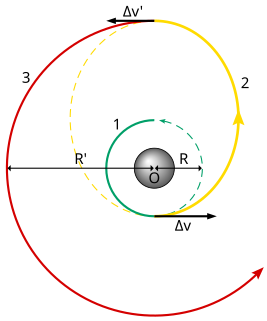
In orbital mechanics, the Hohmann transfer orbit is an elliptical orbit used to transfer between two circular orbits of different radii around a central body in the same plane that is sometimes tangential to both. The Hohmann transfer often uses the lowest possible amount of propellant in traveling between these orbits, but bi-elliptic transfers can use less in some cases.

Orbital mechanics or astrodynamics is the application of ballistics and celestial mechanics to the practical problems concerning the motion of rockets and other spacecraft. The motion of these objects is usually calculated from Newton's laws of motion and law of universal gravitation. Orbital mechanics is a core discipline within space-mission design and control.

In astrodynamics or celestial mechanics a parabolic trajectory is a Kepler orbit with the eccentricity equal to 1 and is an unbound orbit that is exactly on the border between elliptical and hyperbolic. When moving away from the source it is called an escape orbit, otherwise a capture orbit. It is also sometimes referred to as a C3 = 0 orbit (see Characteristic energy).

In astrodynamics or celestial mechanics, a hyperbolic trajectory is the trajectory of any object around a central body with more than enough speed to escape the central object's gravitational pull. The name derives from the fact that according to Newtonian theory such an orbit has the shape of a hyperbola. In more technical terms this can be expressed by the condition that the orbital eccentricity is greater than one.
In astrodynamics, the characteristic energy is a measure of the excess specific energy over that required to just barely escape from a massive body. The units are length2 time−2, i.e. velocity squared, or energy per mass.

In astrodynamics or celestial mechanics, an elliptic orbit or elliptical orbit is a Kepler orbit with an eccentricity of less than 1; this includes the special case of a circular orbit, with eccentricity equal to 0. In a stricter sense, it is a Kepler orbit with the eccentricity greater than 0 and less than 1. In a wider sense, it is a Kepler's orbit with negative energy. This includes the radial elliptic orbit, with eccentricity equal to 1.

A circular orbit is an orbit with a fixed distance around the barycenter; that is, in the shape of a circle.
In celestial mechanics, the specific relative angular momentum of a body is the angular momentum of that body divided by its mass. In the case of two orbiting bodies it is the vector product of their relative position and relative velocity, divided by the mass of the body in question.

In the gravitational two-body problem, the specific orbital energy of two orbiting bodies is the constant sum of their mutual potential energy and their total kinetic energy, divided by the reduced mass. According to the orbital energy conservation equation, it does not vary with time:
In astrodynamics an orbit equation defines the path of orbiting body around central body relative to , without specifying position as a function of time. Under standard assumptions, a body moving under the influence of a force, directed to a central body, with a magnitude inversely proportional to the square of the distance, has an orbit that is a conic section with the central body located at one of the two foci, or the focus.

In astrodynamics, the vis-viva equation, also referred to as orbital-energy-invariance law, is one of the equations that model the motion of orbiting bodies. It is the direct result of the principle of conservation of mechanical energy which applies when the only force acting on an object is its own weight.

A sphere of influence (SOI) in astrodynamics and astronomy is the oblate-spheroid-shaped region around a celestial body where the primary gravitational influence on an orbiting object is that body. This is usually used to describe the areas in the Solar System where planets dominate the orbits of surrounding objects such as moons, despite the presence of the much more massive but distant Sun. In the patched conic approximation, used in estimating the trajectories of bodies moving between the neighbourhoods of different masses using a two body approximation, ellipses and hyperbolae, the SOI is taken as the boundary where the trajectory switches which mass field it is influenced by.
In orbital mechanics, mean motion is the angular speed required for a body to complete one orbit, assuming constant speed in a circular orbit which completes in the same time as the variable speed, elliptical orbit of the actual body. The concept applies equally well to a small body revolving about a large, massive primary body or to two relatively same-sized bodies revolving about a common center of mass. While nominally a mean, and theoretically so in the case of two-body motion, in practice the mean motion is not typically an average over time for the orbits of real bodies, which only approximate the two-body assumption. It is rather the instantaneous value which satisfies the above conditions as calculated from the current gravitational and geometric circumstances of the body's constantly-changing, perturbed orbit.

Spacecraft flight dynamics is the application of mechanical dynamics to model how the external forces acting on a space vehicle or spacecraft determine its flight path. These forces are primarily of three types: propulsive force provided by the vehicle's engines; gravitational force exerted by the Earth and other celestial bodies; and aerodynamic lift and drag.
A canonical unit is a unit of measurement agreed upon as default in a certain context.

In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the two most widely separated points of the perimeter. The semi-major axis is the longest semidiameter or one half of the major axis, and thus runs from the centre, through a focus, and to the perimeter. The semi-minor axis of an ellipse or hyperbola is a line segment that is at right angles with the semi-major axis and has one end at the center of the conic section. For the special case of a circle, the lengths of the semi-axes are both equal to the radius of the circle.

In astrodynamics and celestial mechanics a radial trajectory is a Kepler orbit with zero angular momentum. Two objects in a radial trajectory move directly towards or away from each other in a straight line.
Orbit modeling is the process of creating mathematical models to simulate motion of a massive body as it moves in orbit around another massive body due to gravity. Other forces such as gravitational attraction from tertiary bodies, air resistance, solar pressure, or thrust from a propulsion system are typically modeled as secondary effects. Directly modeling an orbit can push the limits of machine precision due to the need to model small perturbations to very large orbits. Because of this, perturbation methods are often used to model the orbit in order to achieve better accuracy.

























