Spiric section

Last updated May 04, 2024

In geometry, a spiric section, sometimes called a spiric of Perseus, is a quartic plane curve defined by equations of the form

Equivalently, spiric sections can be defined as bicircular quartic curves that are symmetric with respect to the x and y-axes. Spiric sections are included in the family of toric sections and include the family of hippopedes and the family of Cassini ovals. The name is from σπειρα meaning torus in ancient Greek.^[1]

A spiric section is sometimes defined as the curve of intersection of a torus and a plane parallel to its rotational symmetry axis. However, this definition does not include all of the curves given by the previous definition unless imaginary planes are allowed.

Spiric sections were first described by the ancient Greek geometer Perseus in roughly 150 BC, and are assumed to be the first toric sections to be described. The name spiric is due to the ancient notation spira of a torus.,^[2]^[3]

Equations

Start with the usual equation for the torus:

(x^{2}+y^{2}+z^{2}+b^{2}-a^{2})^{2}=4b^{2}(x^{2}+y^{2}).\,

Interchanging y and z so that the axis of revolution is now on the xy-plane, and setting z=c to find the curve of intersection gives

(x^{2}+y^{2}-a^{2}+b^{2}+c^{2})^{2}=4b^{2}(x^{2}+c^{2}).\,

In this formula, the torus is formed by rotating a circle of radius a with its center following another circle of radius b (not necessarily larger than a, self-intersection is permitted). The parameter c is the distance from the intersecting plane to the axis of revolution. There are no spiric sections with c > b + a, since there is no intersection; the plane is too far away from the torus to intersect it.

Expanding the equation gives the form seen in the definition

(x^{2}+y^{2})^{2}=dx^{2}+ey^{2}+f\,

where

d=2(a^{2}+b^{2}-c^{2}),\ e=2(a^{2}-b^{2}-c^{2}),\ f=-(a^{4}+b^{4}+c^{4}-2a^{2}b^{2}-2a^{2}c^{2}-2b^{2}c^{2}).\,

In polar coordinates this becomes

(r^{2}-a^{2}+b^{2}+c^{2})^{2}=4b^{2}(r^{2}\cos ^{2}\theta +c^{2})\,

or

r^{4}=r^{2}(d\cos ^{2}\theta +e\sin ^{2}\theta )+f.

Spiric sections on a spindle torus

Spiric sections on a spindle torus, whose planes intersect the spindle (inner part), consist of an outer and an inner curve (s. picture).

Spiric sections as isoptics

Isoptics of ellipses and hyperbolas are spiric sections. (S. also weblink The Mathematics Enthusiast.)

Examples of spiric sections

Examples include the hippopede and the Cassini oval and their relatives, such as the lemniscate of Bernoulli. The Cassini oval has the remarkable property that the product of distances to two foci are constant. For comparison, the sum is constant in ellipses, the difference is constant in hyperbolae and the ratio is constant in circles.

Related Research Articles

In mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.

In mathematics, the Klein bottle is an example of a non-orientable surface; that is, informally, a one-sided surface which, if traveled upon, could be followed back to the point of origin while flipping the traveler upside down. More formally, the Klein bottle is a two-dimensional manifold on which one cannot define a normal vector at each point that varies continuously over the whole manifold. Other related non-orientable surfaces include the Möbius strip and the real projective plane. While a Möbius strip is a surface with a boundary, a Klein bottle has no boundary. For comparison, a sphere is an orientable surface with no boundary.

A sphere is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. Formally, a sphere is the set of points that are all at the same distance $r$ from a given point in three-dimensional space. That given point is the center of the sphere, and $r$ is the sphere's radius. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians.

In mathematics, a great circle or orthodrome is the circular intersection of a sphere and a plane passing through the sphere's center point.

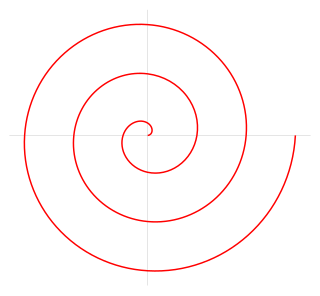
The Archimedean spiral (also known as the arithmetic spiral) is a spiral named after the 3rd-century BC Greek mathematician Archimedes. It is the locus corresponding to the locations over time of a point moving away from a fixed point with a constant speed along a line that rotates with constant angular velocity. Equivalently, in polar coordinates $(r, θ)$ it can be described by the equation

<span class="mw-page-title-main">Ellipsoid</span> Quadric surface that looks like a deformed sphere

An ellipsoid is a surface that can be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation.

In geometry, the lemniscate of Bernoulli is a plane curve defined from two given points $F 1$ and $F 2$ , known as foci, at distance $2 c$ from each other as the locus of points $P$ so that $PF 1 \cdot PF 2 = c 2$ . The curve has a shape similar to the numeral 8 and to the ∞ symbol. Its name is from lemniscatus, which is Latin for "decorated with hanging ribbons". It is a special case of the Cassini oval and is a rational algebraic curve of degree 4.

A 3D projection is a design technique used to display a three-dimensional (3D) object on a two-dimensional (2D) surface. These projections rely on visual perspective and aspect analysis to project a complex object for viewing capability on a simpler plane.

A surface of revolution is a surface in Euclidean space created by rotating a curve one full revolution around an axis of rotation . The volume bounded by the surface created by this revolution is the solid of revolution.

In geometry, the cissoid of Diocles is a cubic plane curve notable for the property that it can be used to construct two mean proportionals to a given ratio. In particular, it can be used to double a cube. It can be defined as the cissoid of a circle and a line tangent to it with respect to the point on the circle opposite to the point of tangency. In fact, the curve family of cissoids is named for this example and some authors refer to it simply as the cissoid. It has a single cusp at the pole, and is symmetric about the diameter of the circle which is the line of tangency of the cusp. The line is an asymptote. It is a member of the conchoid of de Sluze family of curves and in form it resembles a tractrix.

In geometry, a cissoid is a plane curve generated from two given curves $C 1$ , $C 2$ and a point $O$ . Let $L$ be a variable line passing through $O$ and intersecting $C 1$ at $P 1$ and $C 2$ at $P 2$ . Let $P$ be the point on $L$ so that $Then the locus of such points P is defined to be the cissoid of the curves C 1, C 2 relative to O .$

<span class="mw-page-title-main">Cassini oval</span> Class of quartic plane curves

In geometry, a Cassini oval is a quartic plane curve defined as the locus of points in the plane such that the product of the distances to two fixed points (foci) is constant. This may be contrasted with an ellipse, for which the sum of the distances is constant, rather than the product. Cassini ovals are the special case of polynomial lemniscates when the polynomial used has degree 2.

<span class="mw-page-title-main">Hippopede</span> Plane curves of the form (x² + y²)² = cx² + dy²

In geometry, a hippopede is a plane curve determined by an equation of the form

In geometry, a strophoid is a curve generated from a given curve $C$ and points $A$ and $O$ as follows: Let $L$ be a variable line passing through $O$ and intersecting $C$ at $K$ . Now let $P 1$ and $P 2$ be the two points on $L$ whose distance from $K$ is the same as the distance from $A$ to $K$ . The locus of such points $P 1$ and $P 2$ is then the strophoid of $C$ with respect to the pole $O$ and fixed point $A$ . Note that $AP 1$ and $AP 2$ are at right angles in this construction.

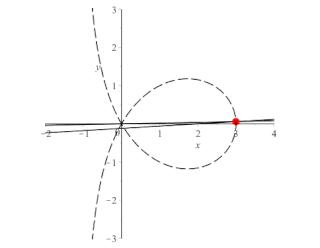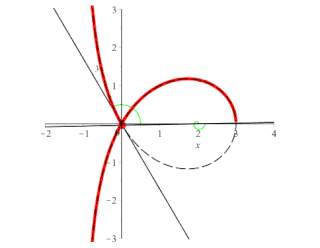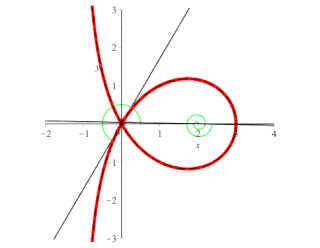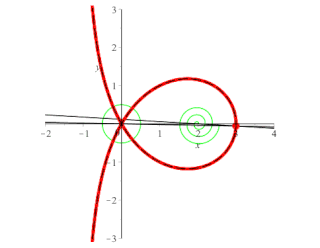
In algebraic geometry, the trisectrix of Maclaurin is a cubic plane curve notable for its trisectrix property, meaning it can be used to trisect an angle. It can be defined as locus of the point of intersection of two lines, each rotating at a uniform rate about separate points, so that the ratio of the rates of rotation is 1:3 and the lines initially coincide with the line between the two points. A generalization of this construction is called a sectrix of Maclaurin. The curve is named after Colin Maclaurin who investigated the curve in 1742.

In algebraic geometry, a quartic plane curve is a plane algebraic curve of the fourth degree. It can be defined by a bivariate quartic equation:

In algebraic geometry, a lemniscate is any of several figure-eight or $\infty$ -shaped curves. The word comes from the Latin lēmniscātus, meaning "decorated with ribbons", from the Greek λημνίσκος (lēmnískos), meaning "ribbon", or which alternatively may refer to the wool from which the ribbons were made.

A toric section is an intersection of a plane with a torus, just as a conic section is the intersection of a plane with a cone. Special cases have been known since antiquity, and the general case was studied by Jean Gaston Darboux.

In inversive geometry, an inverse curve of a given curve $C$ is the result of applying an inverse operation to $C$ . Specifically, with respect to a fixed circle with center $O$ and radius $k$ the inverse of a point $Q$ is the point $P$ for which $P$ lies on the ray $OQ$ and $OP \cdot OQ = k 2$ . The inverse of the curve $C$ is then the locus of $P$ as $Q$ runs over $C$ . The point $O$ in this construction is called the center of inversion, the circle the circle of inversion, and $k$ the radius of inversion.

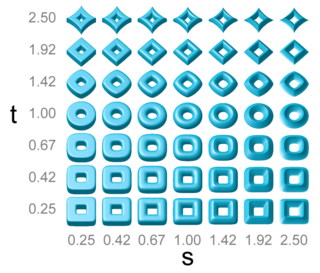
In geometry and computer graphics, a supertoroid or supertorus is usually understood to be a family of doughnut-like surfaces whose shape is defined by mathematical formulas similar to those that define the superellipsoids. The plural of "supertorus" is either supertori or supertoruses.

References

Specific

↑ Brieskorn, Egbert; Knörrer, Horst (1986). Plane algebraic curves. Modern Birkhäuser Classics. Translated by Stillwell, John. Birkhäuser/Springer Basel AG. p. 16. doi:10.1007/978-3-0348-5097-1. ISBN 978-3-0348-0492-9. MR 2975988. The word σπειρα originally meant a coil of rope, and came to refer to the base of a column, which for certain orders of column was shaped as a torus: see Yates, James (1875). "Spira". In Smith, William (ed.). A Dictionary of Greek and Roman Antiquities. London: John Murray.
↑ John Stillwell: Mathematics and Its History, Springer-Verlag, 2010, ISBN 978-1-4419-6053-5, p. 33.
↑ Wilbur R. Knorr: The Ancient Tradition of Geometric Problems , Dover-Publ., New York, 1993, ISBN 0-486-67532-7, p. 268 .

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Brieskorn, Egbert; Knörrer, Horst (1986). Plane algebraic curves. Modern Birkhäuser Classics. Translated by Stillwell, John. Birkhäuser/Springer Basel AG. p. 16. doi:10.1007/978-3-0348-5097-1. ISBN 978-3-0348-0492-9. MR 2975988. The word σπειρα originally meant a coil of rope, and came to refer to the base of a column, which for certain orders of column was shaped as a torus: see Yates, James (1875). "Spira". In Smith, William (ed.). A Dictionary of Greek and Roman Antiquities. London: John Murray.

[2] John Stillwell: Mathematics and Its History, Springer-Verlag, 2010, ISBN 978-1-4419-6053-5, p. 33.

[3] Wilbur R. Knorr: The Ancient Tradition of Geometric Problems , Dover-Publ., New York, 1993, ISBN 0-486-67532-7, p. 268 .

[1]

[2]

[3]