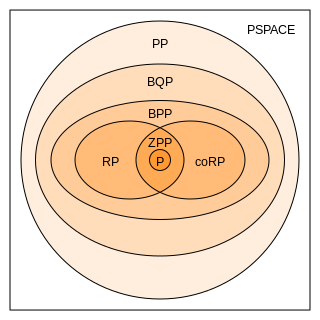
In computational complexity theory, bounded-error quantum polynomial time (BQP) is the class of decision problems solvable by a quantum computer in polynomial time, with an error probability of at most 1/3 for all instances. It is the quantum analogue to the complexity class BPP.
In mathematics, the greatest common divisor (GCD) of two or more integers, which are not all zero, is the largest positive integer that divides each of the integers. For two integers x, y, the greatest common divisor of x and y is denoted . For example, the GCD of 8 and 12 is 4, that is, gcd(8, 12) = 4.
In computational complexity theory, the class NC (for "Nick's Class") is the set of decision problems decidable in polylogarithmic time on a parallel computer with a polynomial number of processors. In other words, a problem with input size n is in NC if there exist constants c and k such that it can be solved in time O((log n)c) using O(nk) parallel processors. Stephen Cook coined the name "Nick's class" after Nick Pippenger, who had done extensive research on circuits with polylogarithmic depth and polynomial size.
In mathematics, a polynomial is a mathematical expression consisting of indeterminates and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. An example of a polynomial of a single indeterminate x is x2 − 4x + 7. An example with three indeterminates is x3 + 2xyz2 − yz + 1.

In mathematics, a square root of a number x is a number y such that ; in other words, a number y whose square is x. For example, 4 and −4 are square roots of 16 because .

In mathematics, a square-free integer (or squarefree integer) is an integer which is divisible by no square number other than 1. That is, its prime factorization has exactly one factor for each prime that appears in it. For example, 10 = 2 ⋅ 5 is square-free, but 18 = 2 ⋅ 3 ⋅ 3 is not, because 18 is divisible by 9 = 32. The smallest positive square-free numbers are
In theoretical computer science, communication complexity studies the amount of communication required to solve a problem when the input to the problem is distributed among two or more parties. The study of communication complexity was first introduced by Andrew Yao in 1979, while studying the problem of computation distributed among several machines. The problem is usually stated as follows: two parties each receive a -bit string and . The goal is for Alice to compute the value of a certain function, , that depends on both and , with the least amount of communication between them.

In mathematics, factorization (or factorisation, see English spelling differences) or factoring consists of writing a number or another mathematical object as a product of several factors, usually smaller or simpler objects of the same kind. For example, 3 × 5 is an integer factorization of 15, and (x – 2)(x + 2) is a polynomial factorization of x2 – 4.

In mathematics, a root of unity, occasionally called a de Moivre number, is any complex number that yields 1 when raised to some positive integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, and the discrete Fourier transform.
An integer programming problem is a mathematical optimization or feasibility program in which some or all of the variables are restricted to be integers. In many settings the term refers to integer linear programming (ILP), in which the objective function and the constraints are linear.

In number theory, the Mertens function is defined for all positive integers n as
In number theory, Dixon's factorization method is a general-purpose integer factorization algorithm; it is the prototypical factor base method. Unlike for other factor base methods, its run-time bound comes with a rigorous proof that does not rely on conjectures about the smoothness properties of the values taken by a polynomial.
Interior-point methods are algorithms for solving linear and non-linear convex optimization problems. IPMs combine two advantages of previously-known algorithms:
In mathematics, the resultant of two polynomials is a polynomial expression of their coefficients that is equal to zero if and only if the polynomials have a common root, or, equivalently, a common factor. In some older texts, the resultant is also called the eliminant.
In mathematical optimization, the ellipsoid method is an iterative method for minimizing convex functions over convex sets. The ellipsoid method generates a sequence of ellipsoids whose volume uniformly decreases at every step, thus enclosing a minimizer of a convex function.
In mathematics, a univariate polynomial of degree n with real or complex coefficients has n complex roots, if counted with their multiplicities. They form a multiset of n points in the complex plane. This article concerns the geometry of these points, that is the information about their localization in the complex plane that can be deduced from the degree and the coefficients of the polynomial.
In computational complexity theory, arithmetic circuits are the standard model for computing polynomials. Informally, an arithmetic circuit takes as inputs either variables or numbers, and is allowed to either add or multiply two expressions it has already computed. Arithmetic circuits provide a formal way to understand the complexity of computing polynomials. The basic type of question in this line of research is "what is the most efficient way to compute a given polynomial ?"
In applied mathematics, Graver bases enable iterative solutions of linear and various nonlinear integer programming problems in polynomial time. They were introduced by Jack E. Graver. Their connection to the theory of Gröbner bases was discussed by Bernd Sturmfels. The algorithmic theory of Graver bases and its application to integer programming is described by Shmuel Onn.
Short integer solution (SIS) and ring-SIS problems are two average-case problems that are used in lattice-based cryptography constructions. Lattice-based cryptography began in 1996 from a seminal work by Miklós Ajtai who presented a family of one-way functions based on SIS problem. He showed that it is secure in an average case if the shortest vector problem (where for some constant ) is hard in a worst-case scenario.
In mathematics and computer science, polynomial evaluation refers to computation of the value of a polynomial when its indeterminates are substituted for some values. In other words, evaluating the polynomial at consists of computing See also Polynomial ring § Polynomial evaluation



























