In mathematics, especially in order theory, the cofinality cf(A) of a partially ordered set A is the least of the cardinalities of the cofinal subsets of A.
In mathematical logic, model theory is the study of the relationship between formal theories, and their models. The aspects investigated include the number and size of models of a theory, the relationship of different models to each other, and their interaction with the formal language itself. In particular, model theorists also investigate the sets that can be defined in a model of a theory, and the relationship of such definable sets to each other. As a separate discipline, model theory goes back to Alfred Tarski, who first used the term "Theory of Models" in publication in 1954. Since the 1970s, the subject has been shaped decisively by Saharon Shelah's stability theory.
In mathematics, a topological space is called separable if it contains a countable, dense subset; that is, there exists a sequence of elements of the space such that every nonempty open subset of the space contains at least one element of the sequence.
In mathematics, an uncountable set is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger than that of the set of all natural numbers.
In mathematics, a Mahlo cardinal is a certain kind of large cardinal number. Mahlo cardinals were first described by Paul Mahlo. As with all large cardinals, none of these varieties of Mahlo cardinals can be proven to exist by ZFC.
In set theory, a branch of mathematics, a Q-indescribable cardinal is a certain kind of large cardinal number that is hard to axiomatize in some language Q. There are many different types of indescribable cardinals corresponding to different choices of languages Q. They were introduced by Hanf & Scott (1961).
In set theory, a Woodin cardinal is a cardinal number such that for all functions

In mathematics, particularly in set theory, the aleph numbers are a sequence of numbers used to represent the cardinality of infinite sets that can be well-ordered. They were introduced by the mathematician Georg Cantor and are named after the symbol he used to denote them, the Semitic letter aleph.
In mathematics, limit cardinals are certain cardinal numbers. A cardinal number λ is a weak limit cardinal if λ is neither a successor cardinal nor zero. This means that one cannot "reach" λ from another cardinal by repeated successor operations. These cardinals are sometimes called simply "limit cardinals" when the context is clear.
In set theory, a regular cardinal is a cardinal number that is equal to its own cofinality. More explicitly, this means that is a regular cardinal if and only if every unbounded subset has cardinality . Infinite well-ordered cardinals that are not regular are called singular cardinals. Finite cardinal numbers are typically not called regular or singular.
In mathematics, particularly in set theory, the beth numbers are a certain sequence of infinite cardinal numbers, conventionally written , where is the second Hebrew letter (beth). The beth numbers are related to the aleph numbers, but unless the generalized continuum hypothesis is true, there are numbers indexed by that are not indexed by .
In mathematics, particularly in mathematical logic and set theory, a club set is a subset of a limit ordinal that is closed under the order topology, and is unbounded relative to the limit ordinal. The name club is a contraction of "closed and unbounded".
In mathematics, particularly in set theory, if is a regular uncountable cardinal then the filter of all sets containing a club subset of is a -complete filter closed under diagonal intersection called the club filter.
In set theory, the singular cardinals hypothesis (SCH) arose from the question of whether the least cardinal number for which the generalized continuum hypothesis (GCH) might fail could be a singular cardinal.
In the mathematical field of set theory, the proper forcing axiom (PFA) is a significant strengthening of Martin's axiom, where forcings with the countable chain condition (ccc) are replaced by proper forcings.
In set theory, an extender is a system of ultrafilters which represents an elementary embedding witnessing large cardinal properties. A nonprincipal ultrafilter is the most basic case of an extender.
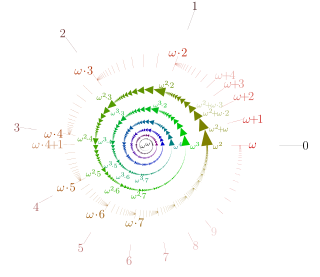
In set theory, an ordinal number, or ordinal, is a generalization of ordinal numerals aimed to extend enumeration to infinite sets.
This is a glossary of set theory.
In mathematics, a polyadic space is a topological space that is the image under a continuous function of a topological power of an Alexandroff one-point compactification of a discrete space.




































