Subgraph isomorphism problem

Last updated May 20, 2024

In theoretical computer science, the subgraph isomorphism problem is a computational task in which two graphs G and H are given as input, and one must determine whether G contains a subgraph that is isomorphic to H. Subgraph isomorphism is a generalization of both the maximum clique problem and the problem of testing whether a graph contains a Hamiltonian cycle, and is therefore NP-complete.^[1] However certain other cases of subgraph isomorphism may be solved in polynomial time.^[2]

Decision problem and computational complexity

To prove subgraph isomorphism is NP-complete, it must be formulated as a decision problem. The input to the decision problem is a pair of graphs G and H. The answer to the problem is positive if H is isomorphic to a subgraph of G, and negative otherwise.

Formal question:

Let $G=(V,E)$ , $H=(V^{\prime },E^{\prime })$ be graphs. Is there a subgraph $G_{0}=(V_{0},E_{0})\mid V_{0}\subseteq V,E_{0}\subseteq E\cap (V_{0}\times V_{0})$ such that $G_{0}\cong H$ ? I. e., does there exist a bijection $f\colon V_{0}\rightarrow V^{\prime }$ such that $\{\,v_{1},v_{2}\,\}\in E_{0}\iff \{\,f(v_{1}),f(v_{2})\,\}\in E^{\prime }$ ?

The proof of subgraph isomorphism being NP-complete is simple and based on reduction of the clique problem, an NP-complete decision problem in which the input is a single graph G and a number k, and the question is whether G contains a complete subgraph with k vertices. To translate this to a subgraph isomorphism problem, simply let H be the complete graph K_k; then the answer to the subgraph isomorphism problem for G and H is equal to the answer to the clique problem for G and k. Since the clique problem is NP-complete, this polynomial-time many-one reduction shows that subgraph isomorphism is also NP-complete.^[3]

An alternative reduction from the Hamiltonian cycle problem translates a graph G which is to be tested for Hamiltonicity into the pair of graphs G and H, where H is a cycle having the same number of vertices as G. Because the Hamiltonian cycle problem is NP-complete even for planar graphs, this shows that subgraph isomorphism remains NP-complete even in the planar case.^[4]

Subgraph isomorphism is a generalization of the graph isomorphism problem, which asks whether G is isomorphic to H: the answer to the graph isomorphism problem is true if and only if G and H both have the same numbers of vertices and edges and the subgraph isomorphism problem for G and H is true. However the complexity-theoretic status of graph isomorphism remains an open question.

In the context of the Aanderaa–Karp–Rosenberg conjecture on the query complexity of monotone graph properties, Gröger (1992) showed that any subgraph isomorphism problem has query complexity Ω(n^3/2); that is, solving the subgraph isomorphism requires an algorithm to check the presence or absence in the input of Ω(n^3/2) different edges in the graph.^[5]

Algorithms

Ullmann (1976) describes a recursive backtracking procedure for solving the subgraph isomorphism problem. Although its running time is, in general, exponential, it takes polynomial time for any fixed choice of H (with a polynomial that depends on the choice of H). When G is a planar graph (or more generally a graph of bounded expansion) and H is fixed, the running time of subgraph isomorphism can be reduced to linear time.^[2]

Ullmann (2010) is a substantial update to the 1976 subgraph isomorphism algorithm paper.

Cordella (2004) proposed in 2004 another algorithm based on Ullmann's, VF2, which improves the refinement process using different heuristics and uses significantly less memory.

Bonnici & Giugno (2013) proposed a better algorithm, which improves the initial order of the vertices using some heuristics.

The current state of the art solver for moderately-sized, hard instances is the Glasgow Subgraph Solver (McCreesh, Prosser & Trimble (2020)).^[6] This solver adopts a constraint programming approach, using bit-parallel data structures and specialized propagation algorithms for performance. It supports most common variations of the problem and is capable of counting or enumerating solutions as well as deciding whether one exists.

For large graphs, state-of-the art algorithms include CFL-Match and Turboiso, and extensions thereupon such as DAF by Han et al. (2019).

Applications

As subgraph isomorphism has been applied in the area of cheminformatics to find similarities between chemical compounds from their structural formula; often in this area the term substructure search is used.^[7] A query structure is often defined graphically using a structure editor program; SMILES based database systems typically define queries using SMARTS, a SMILES extension.

The closely related problem of counting the number of isomorphic copies of a graph H in a larger graph G has been applied to pattern discovery in databases,^[8] the bioinformatics of protein-protein interaction networks,^[9] and in exponential random graph methods for mathematically modeling social networks.^[10]

Ohlrich et al. (1993) describe an application of subgraph isomorphism in the computer-aided design of electronic circuits. Subgraph matching is also a substep in graph rewriting (the most runtime-intensive), and thus offered by graph rewrite tools.

The problem is also of interest in artificial intelligence, where it is considered part of an array of pattern matching in graphs problems; an extension of subgraph isomorphism known as graph mining is also of interest in that area.^[11]

Notes

↑ The original Cook (1971) paper that proves the Cook–Levin theorem already showed subgraph isomorphism to be NP-complete, using a reduction from 3-SAT involving cliques.
1 2 Eppstein (1999); Nešetřil & Ossona de Mendez (2012)
↑ Wegener, Ingo (2005), Complexity Theory: Exploring the Limits of Efficient Algorithms, Springer, p. 81, ISBN 9783540210450 .
↑ de la Higuera, Colin; Janodet, Jean-Christophe; Samuel, Émilie; Damiand, Guillaume; Solnon, Christine (2013), "Polynomial algorithms for open plane graph and subgraph isomorphisms" (PDF), Theoretical Computer Science, 498: 76–99, doi: 10.1016/j.tcs.2013.05.026 , MR 3083515, It is known since the mid-70's that the isomorphism problem is solvable in polynomial time for plane graphs. However, it has also been noted that the subisomorphism problem is still N P-complete, in particular because the Hamiltonian cycle problem is NP-complete for planar graphs.
↑ Here Ω invokes Big Omega notation.
↑ For an experimental evaluation, see Solnon (2019).
↑ Ullmann (1976)
↑ Kuramochi & Karypis (2001).
↑ Pržulj, Corneil & Jurisica (2006).
↑ Snijders et al. (2006).
↑ http://www.aaai.org/Papers/Symposia/Fall/2006/FS-06-02/FS06-02-007.pdf; expanded version at https://e-reports-ext.llnl.gov/pdf/332302.pdf

Related Research Articles

In graph theory, an isomorphism of graphsG and H is a bijection between the vertex sets of G and H

In computer science, the clique problem is the computational problem of finding cliques in a graph. It has several different formulations depending on which cliques, and what information about the cliques, should be found. Common formulations of the clique problem include finding a maximum clique, finding a maximum weight clique in a weighted graph, listing all maximal cliques, and solving the decision problem of testing whether a graph contains a clique larger than a given size.

In theoretical computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by the algorithm, supposing that each elementary operation takes a fixed amount of time to perform. Thus, the amount of time taken and the number of elementary operations performed by the algorithm are taken to be related by a constant factor.

In graph theory, an independent set, stable set, coclique or anticlique is a set of vertices in a graph, no two of which are adjacent. That is, it is a set $of vertices such that for every two vertices in, there is no edge connecting the two. Equivalently, each edge in the graph has at most one endpoint in . A set is independent if and only if it is a clique in the graph's complement. The size of an independent set is the number of vertices it contains. Independent sets have also been called "internally stable sets", of which "stable set" is a shortening.$

In the mathematical discipline of graph theory, a matching or independent edge set in an undirected graph is a set of edges without common vertices. In other words, a subset of the edges is a matching if each vertex appears in at most one edge of that matching. Finding a matching in a bipartite graph can be treated as a network flow problem.

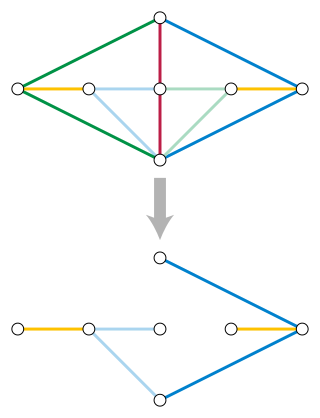
In graph theory, a cograph, or complement-reducible graph, or P₄-free graph, is a graph that can be generated from the single-vertex graph K₁ by complementation and disjoint union. That is, the family of cographs is the smallest class of graphs that includes K₁ and is closed under complementation and disjoint union.

<span class="mw-page-title-main">Graph property</span> Property of graphs that depends only on abstract structure

In graph theory, a graph property or graph invariant is a property of graphs that depends only on the abstract structure, not on graph representations such as particular labellings or drawings of the graph.

In the mathematical discipline of graph theory, a feedback vertex set (FVS) of a graph is a set of vertices whose removal leaves a graph without cycles. Equivalently, each FVS contains at least one vertex of any cycle in the graph. The feedback vertex set number of a graph is the size of a smallest feedback vertex set. The minimum feedback vertex set problem is an NP-complete problem; it was among the first problems shown to be NP-complete. It has wide applications in operating systems, database systems, and VLSI chip design.

The graph isomorphism problem is the computational problem of determining whether two finite graphs are isomorphic.

In graph theory and theoretical computer science, a maximum common induced subgraph of two graphs G and H is a graph that is an induced subgraph of both G and H, and that has as many vertices as possible.

In complexity theory and graph theory, induced subgraph isomorphism is an NP-complete decision problem that involves finding a given graph as an induced subgraph of a larger graph.

<span class="mw-page-title-main">Modular product of graphs</span> Binary operation in graph theory

In graph theory, the modular product of graphs $G$ and $H$ is a graph formed by combining $G$ and $H$ that has applications to subgraph isomorphism. It is one of several different kinds of graph products that have been studied, generally using the same vertex set but with different rules for determining which edges to include.

In the mathematical field of graph theory, an automorphism of a graph is a form of symmetry in which the graph is mapped onto itself while preserving the edge–vertex connectivity.

In graph theory, the clique-width of a graph $G$ is a parameter that describes the structural complexity of the graph; it is closely related to treewidth, but unlike treewidth it can be small for dense graphs. It is defined as the minimum number of labels needed to construct $G$ by means of the following 4 operations :

Creation of a new vertex $v$ with label $i$ (denoted by $i (v)$ )
Disjoint union of two labeled graphs $G$ and $H$ (denoted by $)$
Joining by an edge every vertex labeled $i$ to every vertex labeled $j$ (denoted by $η (i, j)$ ), where $i \neq j$
Renaming label $i$ to label $j$ (denoted by $ρ (i, j)$ )

In graph theory, a clique cover or partition into cliques of a given undirected graph is a partition of the vertices into cliques, subsets of vertices within which every two vertices are adjacent. A minimum clique cover is a clique cover that uses as few cliques as possible. The minimum $k$ for which a clique cover exists is called the clique cover number of the given graph.

In computational complexity theory, a problem is NP-complete when:

It is a decision problem, meaning that for any input to the problem, the output is either "yes" or "no".
When the answer is "yes", this can be demonstrated through the existence of a short solution.
The correctness of each solution can be verified quickly and a brute-force search algorithm can find a solution by trying all possible solutions.
The problem can be used to simulate every other problem for which we can verify quickly that a solution is correct. In this sense, NP-complete problems are the hardest of the problems to which solutions can be verified quickly. If we could find solutions of some NP-complete problem quickly, we could quickly find the solutions of every other problem to which a given solution can be easily verified.

In graph theory and computer science, a dense subgraph is a subgraph with many edges per vertex. This is formalized as follows: let $G = (V, E)$ be an undirected graph and let $S = (V S, E S)$ be a subgraph of $G$ . Then the density of $S$ is defined to be:

In theoretical computer science, Baker's technique is a method for designing polynomial-time approximation schemes (PTASs) for problems on planar graphs. It is named after Brenda Baker, who announced it in a 1983 conference and published it in the Journal of the ACM in 1994.

In combinatorial optimization, the matroid parity problem is a problem of finding the largest independent set of paired elements in a matroid. The problem was formulated by Lawler (1976) as a common generalization of graph matching and matroid intersection. It is also known as polymatroid matching, or the matchoid problem.

References

Cook, S. A. (1971), "The complexity of theorem-proving procedures", Proc. 3rd ACM Symposium on Theory of Computing, pp. 151–158, doi: 10.1145/800157.805047 , S2CID 7573663 .
Eppstein, David (1999), "Subgraph isomorphism in planar graphs and related problems" (PDF), Journal of Graph Algorithms and Applications , 3 (3): 1–27, arXiv: cs.DS/9911003 , doi:10.7155/jgaa.00014, S2CID 2303110 .
Garey, Michael R.; Johnson, David S. (1979), Computers and Intractability: A Guide to the Theory of NP-Completeness, W.H. Freeman, ISBN 978-0-7167-1045-5 . A1.4: GT48, pg.202.
Gröger, Hans Dietmar (1992), "On the randomized complexity of monotone graph properties" (PDF), Acta Cybernetica, 10 (3): 119–127.
Han, Myoungji; Kim, Hyunjoon; Gu, Geonmo; Park, Kunsoo; Han, Wookshin (2019), "Efficient Subgraph Matching: Harmonizing Dynamic Programming, Adaptive Matching Order, and Failing Set Together", SIGMOD, doi:10.1145/3299869.3319880, S2CID 195259296
Kuramochi, Michihiro; Karypis, George (2001), "Frequent subgraph discovery", 1st IEEE International Conference on Data Mining, p. 313, CiteSeerX 10.1.1.22.4992 , doi:10.1109/ICDM.2001.989534, ISBN 978-0-7695-1119-1, S2CID 8684662 .
Ohlrich, Miles; Ebeling, Carl; Ginting, Eka; Sather, Lisa (1993), "SubGemini: identifying subcircuits using a fast subgraph isomorphism algorithm", Proceedings of the 30th international Design Automation Conference, pp. 31–37, doi: 10.1145/157485.164556 , ISBN 978-0-89791-577-9, S2CID 5889119 .
Nešetřil, Jaroslav; Ossona de Mendez, Patrice (2012), "18.3 The subgraph isomorphism problem and Boolean queries", Sparsity: Graphs, Structures, and Algorithms, Algorithms and Combinatorics, vol. 28, Springer, pp. 400–401, doi:10.1007/978-3-642-27875-4, ISBN 978-3-642-27874-7, MR 2920058 .
Pržulj, N.; Corneil, D. G.; Jurisica, I. (2006), "Efficient estimation of graphlet frequency distributions in protein–protein interaction networks", Bioinformatics, 22 (8): 974–980, doi: 10.1093/bioinformatics/btl030 , PMID 16452112 .
Snijders, T. A. B.; Pattison, P. E.; Robins, G.; Handcock, M. S. (2006), "New specifications for exponential random graph models", Sociological Methodology, 36 (1): 99–153, CiteSeerX 10.1.1.62.7975 , doi:10.1111/j.1467-9531.2006.00176.x, S2CID 10800726 .
Ullmann, Julian R. (1976), "An algorithm for subgraph isomorphism", Journal of the ACM , 23 (1): 31–42, doi: 10.1145/321921.321925 , S2CID 17268751 .
Jamil, Hasan (2011), "Computing Subgraph Isomorphic Queries using Structural Unification and Minimum Graph Structures", 26th ACM Symposium on Applied Computing, pp. 1058–1063.
Ullmann, Julian R. (2010), "Bit-vector algorithms for binary constraint satisfaction and subgraph isomorphism", Journal of Experimental Algorithmics , 15: 1.1, CiteSeerX 10.1.1.681.8766 , doi:10.1145/1671970.1921702, S2CID 15021184 .
Cordella, Luigi P. (2004), "A (sub) graph isomorphism algorithm for matching large graphs", IEEE Transactions on Pattern Analysis and Machine Intelligence, 26 (10): 1367–1372, CiteSeerX 10.1.1.101.5342 , doi:10.1109/tpami.2004.75, PMID 15641723, S2CID 833657
Bonnici, V.; Giugno, R. (2013), "A subgraph isomorphism algorithm and its application to biochemical data", BMC Bioinformatics, 14(Suppl7) (13): S13, doi: 10.1186/1471-2105-14-s7-s13 , PMC 3633016 , PMID 23815292
Carletti, V.; Foggia, P.; Saggese, A.; Vento, M. (2018), "Challenging the time complexity of exact subgraph isomorphism for huge and dense graphs with VF3", IEEE Transactions on Pattern Analysis and Machine Intelligence, 40 (4): 804–818, doi:10.1109/TPAMI.2017.2696940, PMID 28436848, S2CID 3709576
Solnon, Christine (2019), "Experimental Evaluation of Subgraph Isomorphism Solvers" (PDF), Graph-Based Representations in Pattern Recognition - 12th IAPR-TC-15 International Workshop, GbRPR 2019, Tours, France, June 19-21, 2019, Proceedings, Lecture Notes in Computer Science, vol. 11510, Springer, pp. 1–13, doi:10.1007/978-3-030-20081-7_1, ISBN 978-3-030-20080-0, S2CID 128270779
McCreesh, Ciaran; Prosser, Patrick; Trimble, James (2020), "The Glasgow Subgraph Solver: Using Constraint Programming to Tackle Hard Subgraph Isomorphism Problem Variants", Graph Transformation - 13th International Conference, ICGT 2020, Held as Part of STAF 2020, Bergen, Norway, June 25-26, 2020, Proceedings, Lecture Notes in Computer Science, vol. 12150, Springer, pp. 316–324, doi: 10.1007/978-3-030-51372-6_19 , ISBN 978-3-030-51371-9

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] The original Cook (1971) paper that proves the Cook–Levin theorem already showed subgraph isomorphism to be NP-complete, using a reduction from 3-SAT involving cliques.

[e99-2] 1 2 Eppstein (1999); Nešetřil & Ossona de Mendez (2012)

[3] Wegener, Ingo (2005), Complexity Theory: Exploring the Limits of Efficient Algorithms, Springer, p. 81, ISBN 9783540210450 .

[4] Higuera, Colin; Janodet, Jean-Christophe; Samuel, Émilie; Damiand, Guillaume; Solnon, Christine (2013), "Polynomial algorithms for open plane graph and subgraph isomorphisms" (PDF), Theoretical Computer Science, 498: 76–99, doi: 10.1016/j.tcs.2013.05.026 , MR 3083515, It is known since the mid-70's that the isomorphism problem is solvable in polynomial time for plane graphs. However, it has also been noted that the subisomorphism problem is still N P-complete, in particular because the Hamiltonian cycle problem is NP-complete for planar graphs.

[5] Here Ω invokes Big Omega notation.

[6] For an experimental evaluation, see Solnon (2019).

[7] Ullmann (1976)

[8] Kuramochi & Karypis (2001).

[9] Pržulj, Corneil & Jurisica (2006).

[10] Snijders et al. (2006).

[11] ttp://www.aaai.org/Papers/Symposia/Fall/2006/FS-06-02/FS06-02-007.pdf; expanded version at https://e-reports-ext.llnl.gov/pdf/332302.pdf

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]