In set theory, a supertransitive class is a transitive class [1] which includes as a subset the power set of each of its elements.
Formally, let A be a transitive class. Then A is supertransitive if and only if
Here P(x) denotes the power set of x. [3]
In mathematics, the axiom of regularity is an axiom of Zermelo–Fraenkel set theory that states that every non-empty set A contains an element that is disjoint from A. In first-order logic, the axiom reads:
In mathematics, a binary relation over sets X and Y is a subset of the Cartesian product ; that is, it is a set of ordered pairs (x, y) consisting of elements x in X and y in Y. It encodes the common concept of relation: an element x is related to an element y, if and only if the pair (x, y) belongs to the set of ordered pairs that defines the binary relation. A binary relation is the most studied special case n = 2 of an n-ary relation over sets X1, ..., Xn, which is a subset of the Cartesian product
Naive set theory is any of several theories of sets used in the discussion of the foundations of mathematics. Unlike axiomatic set theories, which are defined using formal logic, naive set theory is defined informally, in natural language. It describes the aspects of mathematical sets familiar in discrete mathematics, and suffices for the everyday use of set theory concepts in contemporary mathematics.
In mathematics, an equivalence relation is a binary relation that is reflexive, symmetric and transitive. The relation "is equal to" is the canonical example of an equivalence relation.
In mathematics, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories ensure that the empty set exists by including an axiom of empty set, while in other theories, its existence can be deduced. Many possible properties of sets are vacuously true for the empty set.
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation indicating that, for certain pairs of elements in the set, one of the elements precedes the other in the ordering. The relation itself is called a "partial order." The word partial in the names "partial order" and "partially ordered set" is used as an indication that not every pair of elements needs to be comparable. That is, there may be pairs of elements for which neither element precedes the other in the poset. Partial orders thus generalize total orders, in which every pair is comparable.
In mathematics, the power set of a set S is the set of all subsets of S, including the empty set and S itself. In axiomatic set theory, the existence of the power set of any set is postulated by the axiom of power set. The powerset of S is variously denoted as P(S), 𝒫(S), P(S), (S), ℘(S), or 2S. The notation 2S is used because given any set with exactly two elements, the powerset of S can be identified with the set of all functions from S into that set.
Set theory is the branch of mathematical logic that studies sets, which can be informally described as collections of objects. Although objects of any kind can be collected into a set, set theory, as a branch of mathematics, is mostly concerned with those that are relevant to mathematics as a whole.
In mathematics, the axiom of power set is one of the Zermelo–Fraenkel axioms of axiomatic set theory.
In set theory, Zermelo–Fraenkel set theory, named after mathematicians Ernst Zermelo and Abraham Fraenkel, is an axiomatic system that was proposed in the early twentieth century in order to formulate a theory of sets free of paradoxes such as Russell's paradox. Today, Zermelo–Fraenkel set theory, with the historically controversial axiom of choice (AC) included, is the standard form of axiomatic set theory and as such is the most common foundation of mathematics. Zermelo–Fraenkel set theory with the axiom of choice included is abbreviated ZFC, where C stands for "choice", and ZF refers to the axioms of Zermelo–Fraenkel set theory with the axiom of choice excluded.
In axiomatic set theory and the branches of mathematics and philosophy that use it, the axiom of infinity is one of the axioms of Zermelo–Fraenkel set theory. It guarantees the existence of at least one infinite set, namely a set containing the natural numbers. It was first published by Ernst Zermelo as part of his set theory in 1908.
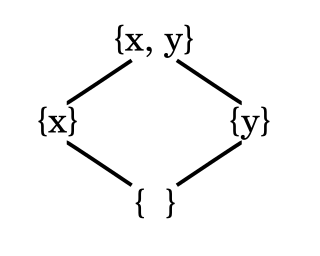
In order theory, a Hasse diagram is a type of mathematical diagram used to represent a finite partially ordered set, in the form of a drawing of its transitive reduction. Concretely, for a partially ordered set (S, ≤) one represents each element of S as a vertex in the plane and draws a line segment or curve that goes upward from x to y whenever y covers x . These curves may cross each other but must not touch any vertices other than their endpoints. Such a diagram, with labeled vertices, uniquely determines its partial order.
In mathematics, in set theory, the constructible universe, denoted by L, is a particular class of sets that can be described entirely in terms of simpler sets. L is the union of the constructible hierarchyLα . It was introduced by Kurt Gödel in his 1938 paper "The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis". In this, he proved that the constructible universe is an inner model of ZF set theory, and also that the axiom of choice and the generalized continuum hypothesis are true in the constructible universe. This shows that both propositions are consistent with the basic axioms of set theory, if ZF itself is consistent. Since many other theorems only hold in systems in which one or both of the propositions is true, their consistency is an important result.
In mathematics, two sets or classes A and B are equinumerous if there exists a one-to-one correspondence between them, that is, if there exists a function from A to B such that for every element y of B, there is exactly one element x of A with f(x) = y. Equinumerous sets are said to have the same cardinality. The study of cardinality is often called equinumerosity (equalness-of-number). The terms equipollence (equalness-of-strength) and equipotence (equalness-of-power) are sometimes used instead.
In mathematics, a Grothendieck universe is a set U with the following properties:
In mathematics, an unordered pair or pair set is a set of the form {a, b}, i.e. a set having two elements a and b with no particular relation between them, where {a, b} = {b, a}. In contrast, an ordered pair (a, b) has a as its first element and b as its second element, which means (a, b) ≠ (b, a).
Gaisi Takeuti was a Japanese mathematician, known for his work in proof theory.
In mathematics, a binary relation over sets X and Y is a subset of the Cartesian product X × Y; that is, it is a set of ordered pairs (x, y) consisting of elements x in X and y in Y. It encodes the common concept of relation: an element x is related to an element y, if and only if the pair (x, y) belongs to the set of ordered pairs that defines the binary relation. A binary relation is the most studied special case n = 2 of an n-ary relation over sets X1, ..., Xn, which is a subset of the Cartesian product X1 × ... × Xn.
In set theory, an ordinal number, or ordinal, is one generalization of the concept of a natural number that is used to describe a way to arrange a collection of objects in order, one after another.
In set theory, a foundational relation on a set or proper class lets each nonempty subset admit a relational minimal element.
