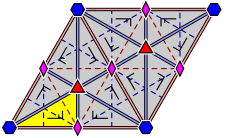
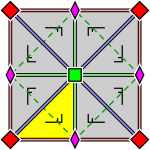
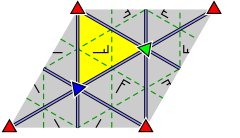
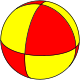
In geometry, an octahedron is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.
In geometry, a Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent regular polygons, and the same number of faces meet at each vertex. There are only five such polyhedra:

In geometry, a tetrahedron, also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the ordinary convex polyhedra and the only one that has fewer than 5 faces.

In Euclidean plane geometry, a rectangle is a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal ; or a parallelogram containing a right angle. A rectangle with four sides of equal length is a square. The term oblong is occasionally used to refer to a non-square rectangle. A rectangle with vertices ABCD would be denoted as ABCD.

Elliptic geometry is an example of a geometry in which Euclid's parallel postulate does not hold. Instead, as in spherical geometry, there are no parallel lines since any two lines must intersect. However, unlike in spherical geometry, two lines are usually assumed to intersect at a single point. Because of this, the elliptic geometry described in this article is sometimes referred to as single elliptic geometry whereas spherical geometry is sometimes referred to as double elliptic geometry.

In mathematics, hyperbolic geometry is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:

A wallpaper is a mathematical object we imagine covering a whole Euclidean plane by repeating a motif indefinitely, in manner that certain isometries keep the drawing unchanged. To a given wallpaper there corresponds a group of such congruent transformations, with function composition as the group operation. Thus, a wallpaper group is in a mathematical classification of a two‑dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art, especially in textiles, tessellations and tiles as well as wallpaper.

In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles. It can also be defined as a rectangle with two equal-length adjacent sides. It is the only regular polygon whose internal angle, central angle, and external angle are all equal (90°), and whose diagonals are all equal in length. A square with vertices ABCD would be denoted ABCD.

Rotational symmetry, also known as radial symmetry in geometry, is the property a shape has when it looks the same after some rotation by a partial turn. An object's degree of rotational symmetry is the number of distinct orientations in which it looks exactly the same for each rotation.

In hyperbolic geometry, a hyperbolic triangle is a triangle in the hyperbolic plane. It consists of three line segments called sides or edges and three points called angles or vertices.
In geometry, a Schwarz triangle, named after Hermann Schwarz, is a spherical triangle that can be used to tile a sphere, possibly overlapping, through reflections in its edges. They were classified in Schwarz (1873).
In group theory and geometry, a reflection group is a discrete group which is generated by a set of reflections of a finite-dimensional Euclidean space. The symmetry group of a regular polytope or of a tiling of the Euclidean space by congruent copies of a regular polytope is necessarily a reflection group. Reflection groups also include Weyl groups and crystallographic Coxeter groups. While the orthogonal group is generated by reflections, it is a continuous group, not a discrete group, and is generally considered separately.
In geometry, orbifold notation is a system, invented by the mathematician William Thurston and promoted by John Conway, for representing types of symmetry groups in two-dimensional spaces of constant curvature. The advantage of the notation is that it describes these groups in a way which indicates many of the groups' properties: in particular, it follows William Thurston in describing the orbifold obtained by taking the quotient of Euclidean space by the group under consideration.

In geometry, the Wythoff symbol is a notation representing a Wythoff construction of a uniform polyhedron or plane tiling within a Schwarz triangle. It was first used by Coxeter, Longuet-Higgins and Miller in their enumeration of the uniform polyhedra. Later the Coxeter diagram was developed to mark uniform polytopes and honeycombs in n-dimensional space within a fundamental simplex.

In geometry, a pentagonal tiling is a tiling of the plane where each individual piece is in the shape of a pentagon.

In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors. It describes a kaleidoscopic construction: each graph "node" represents a mirror and the label attached to a branch encodes the dihedral angle order between two mirrors, that is, the amount by which the angle between the reflective planes can be multiplied to get 180 degrees. An unlabeled branch implicitly represents order-3, and each pair of nodes that is not connected by a branch at all represents a pair of mirrors at order-2.
In geometry, a triangle center is a point in the plane that is in some sense a center of a triangle akin to the centers of squares and circles, that is, a point that is in the middle of the figure by some measure. For example, the centroid, circumcenter, incenter and orthocenter were familiar to the ancient Greeks, and can be obtained by simple constructions.
In the theory of Riemann surfaces and hyperbolic geometry, the triangle group (2,3,7) is particularly important. This importance stems from its connection to Hurwitz surfaces, namely Riemann surfaces of genus g with the largest possible order, 84(g − 1), of its automorphism group.
In geometry, many uniform tilings on sphere, euclidean plane, and hyperbolic plane can be made by Wythoff construction within a fundamental triangle,, defined by internal angles as π/p, π/q, and π/r. Special cases are right triangles. Uniform solutions are constructed by a single generator point with 7 positions within the fundamental triangle, the 3 corners, along the 3 edges, and the triangle interior. All vertices exist at the generator, or a reflected copy of it. Edges exist between a generator point and its image across a mirror. Up to 3 face types exist centered on the fundamental triangle corners. Right triangle domains can have as few as 1 face type, making regular forms, while general triangles have at least 2 triangle types, leading at best to a quasiregular tiling.