
A unit cube, more formally a cube of side 1, is a cube whose sides are 1 unit long. [1] [2] The volume of a 3-dimensional unit cube is 1 cubic unit, and its total surface area is 6 square units. [3]

A unit cube, more formally a cube of side 1, is a cube whose sides are 1 unit long. [1] [2] The volume of a 3-dimensional unit cube is 1 cubic unit, and its total surface area is 6 square units. [3]
The term unit cube or unit hypercube is also used for hypercubes, or "cubes" in n-dimensional spaces, for values of n other than 3 and edge length 1. [1] [2]
Sometimes the term "unit cube" refers in specific to the set [0, 1]n of all n-tuples of numbers in the interval [0, 1]. [1]
The length of the longest diagonal of a unit hypercube of n dimensions is , the square root of n and the (Euclidean) length of the vector (1,1,1,....1,1) in n-dimensional space. [2]

In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets, or sides, with three meeting at each vertex. Viewed from a corner, it is a hexagon and its net is usually depicted as a cross.

Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry, Elements. Euclid's approach consists in assuming a small set of intuitively appealing axioms (postulates) and deducing many other propositions (theorems) from these. Although many of Euclid's results had been stated earlier, Euclid was the first to organize these propositions into a logical system in which each result is proved from axioms and previously proved theorems.
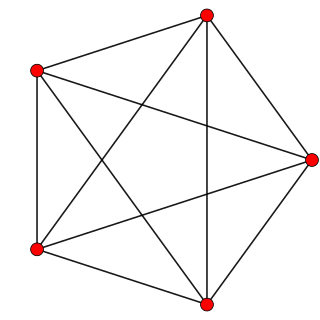
In geometry, a 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower-dimensional polytopal elements: vertices, edges, faces (polygons), and cells (polyhedra). Each face is shared by exactly two cells. The 4-polytopes were discovered by the Swiss mathematician Ludwig Schläfli before 1853.

In geometry, a tesseract or 4-cube is a four-dimensional hypercube, analogous to a two-dimensional square and a three-dimensional cube. Just as the perimeter of the square consists of four edges and the surface of the cube consists of six square faces, the hypersurface of the tesseract consists of eight cubical cells, meeting at right angles. The tesseract is one of the six convex regular 4-polytopes.

In geometry, a hypercube is an n-dimensional analogue of a square and a cube. It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length. A unit hypercube's longest diagonal in n dimensions is equal to .
In solid geometry, a face is a flat surface that forms part of the boundary of a solid object; a three-dimensional solid bounded exclusively by faces is a polyhedron.
In mathematics, a magic hypercube is the k-dimensional generalization of magic squares and magic cubes, that is, an n × n × n × ... × n array of integers such that the sums of the numbers on each pillar (along any axis) as well as on the main space diagonals are all the same. The common sum is called the magic constant of the hypercube, and is sometimes denoted Mk(n). If a magic hypercube consists of the numbers 1, 2, ..., nk, then it has magic number

In mathematics, a regular polytope is a polytope whose symmetry group acts transitively on its flags, thus giving it the highest degree of symmetry. In particular, all its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are themselves regular polytopes of dimension j≤ n.

A polycube is a solid figure formed by joining one or more equal cubes face to face. Polycubes are the three-dimensional analogues of the planar polyominoes. The Soma cube, the Bedlam cube, the Diabolical cube, the Slothouber–Graatsma puzzle, and the Conway puzzle are examples of packing problems based on polycubes.
The curse of dimensionality refers to various phenomena that arise when analyzing and organizing data in high-dimensional spaces that do not occur in low-dimensional settings such as the three-dimensional physical space of everyday experience. The expression was coined by Richard E. Bellman when considering problems in dynamic programming. The curse generally refers to issues that arise when the number of datapoints is small relative to the intrinsic dimension of the data.
Every magic cube may be assigned to one of six magic cube classes, based on the cube characteristics.
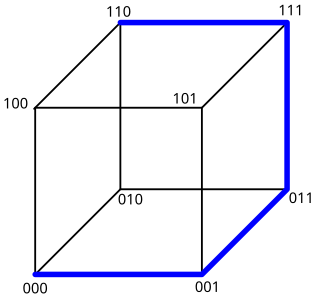
The snake-in-the-box problem in graph theory and computer science deals with finding a certain kind of path along the edges of a hypercube. This path starts at one corner and travels along the edges to as many corners as it can reach. After it gets to a new corner, the previous corner and all of its neighbors must be marked as unusable. The path should never travel to a corner which has been marked unusable.
In geometry, a truncated tesseract is a uniform 4-polytope formed as the truncation of the regular tesseract.
In harmonic analysis in mathematics, a function of bounded mean oscillation, also known as a BMO function, is a real-valued function whose mean oscillation is bounded (finite). The space of functions of bounded mean oscillation (BMO), is a function space that, in some precise sense, plays the same role in the theory of Hardy spaces Hp that the space L∞ of essentially bounded functions plays in the theory of Lp-spaces: it is also called John–Nirenberg space, after Fritz John and Louis Nirenberg who introduced and studied it for the first time.
In five-dimensional geometry, a 5-cube is a name for a five-dimensional hypercube with 32 vertices, 80 edges, 80 square faces, 40 cubic cells, and 10 tesseract 4-faces.

In geometry, a Petrie polygon for a regular polytope of n dimensions is a skew polygon in which every n – 1 consecutive sides belongs to one of the facets. The Petrie polygon of a regular polygon is the regular polygon itself; that of a regular polyhedron is a skew polygon such that every two consecutive sides belongs to one of the faces. Petrie polygons are named for mathematician John Flinders Petrie.
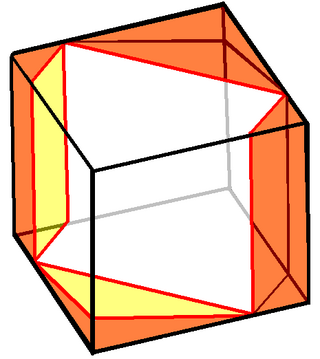
In geometry, Prince Rupert's cube is the largest cube that can pass through a hole cut through a unit cube without splitting it into separate pieces. Its side length is approximately 1.06, 6% larger than the side length 1 of the unit cube through which it passes. The problem of finding the largest square that lies entirely within a unit cube is closely related, and has the same solution.
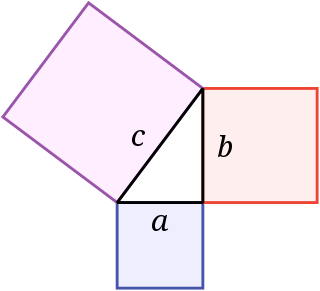
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides.

In geometry, Keller's conjecture is the conjecture that in any tiling of n-dimensional Euclidean space by identical hypercubes, there are two hypercubes that share an entire (n − 1)-dimensional face with each other. For instance, in any tiling of the plane by identical squares, some two squares must share an entire edge, as they do in the illustration.

A Pythagorean tiling or two squares tessellation is a tiling of a Euclidean plane by squares of two different sizes, in which each square touches four squares of the other size on its four sides. Many proofs of the Pythagorean theorem are based on it, explaining its name. It is commonly used as a pattern for floor tiles. When used for this, it is also known as a hopscotch pattern or pinwheel pattern, but it should not be confused with the mathematical pinwheel tiling, an unrelated pattern.