
In physics, the Lorentz transformations are a six-parameter family of linear transformations from a coordinate frame in spacetime to another frame that moves at a constant velocity relative to the former. The respective inverse transformation is then parameterized by the negative of this velocity. The transformations are named after the Dutch physicist Hendrik Lorentz.

The Navier–Stokes equations are partial differential equations which describe the motion of viscous fluid substances. They were named after French engineer and physicist Claude-Louis Navier and the Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes).

The kinetic theory of gases is a simple, historically significant classical model of the thermodynamic behavior of gases, with which many principal concepts of thermodynamics were established. The model describes a gas as a large number of identical submicroscopic particles, all of which are in constant, rapid, random motion. Their size is assumed to be much smaller than the average distance between the particles. The particles undergo random elastic collisions between themselves and with the enclosing walls of the container. The basic version of the model describes the ideal gas, and considers no other interactions between the particles.

In mathematics and physics, the heat equation is a certain partial differential equation. Solutions of the heat equation are sometimes known as caloric functions. The theory of the heat equation was first developed by Joseph Fourier in 1822 for the purpose of modeling how a quantity such as heat diffuses through a given region.
In physics, a Langevin equation is a stochastic differential equation describing how a system evolves when subjected to a combination of deterministic and fluctuating ("random") forces. The dependent variables in a Langevin equation typically are collective (macroscopic) variables changing only slowly in comparison to the other (microscopic) variables of the system. The fast (microscopic) variables are responsible for the stochastic nature of the Langevin equation. One application is to Brownian motion, which models the fluctuating motion of a small particle in a fluid.

In fluid dynamics, the Euler equations are a set of quasilinear partial differential equations governing adiabatic and inviscid flow. They are named after Leonhard Euler. In particular, they correspond to the Navier–Stokes equations with zero viscosity and zero thermal conductivity.
A continuity equation or transport equation is an equation that describes the transport of some quantity. It is particularly simple and powerful when applied to a conserved quantity, but it can be generalized to apply to any extensive quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described using continuity equations.
In mathematics, an Euler–Cauchy equation, or Cauchy–Euler equation, or simply Euler's equation is a linear homogeneous ordinary differential equation with variable coefficients. It is sometimes referred to as an equidimensional equation. Because of its particularly simple equidimensional structure, the differential equation can be solved explicitly.
A theoretical plate in many separation processes is a hypothetical zone or stage in which two phases, such as the liquid and vapor phases of a substance, establish an equilibrium with each other. Such equilibrium stages may also be referred to as an equilibrium stage, ideal stage, or a theoretical tray. The performance of many separation processes depends on having series of equilibrium stages and is enhanced by providing more such stages. In other words, having more theoretical plates increases the efficiency of the separation process be it either a distillation, absorption, chromatographic, adsorption or similar process.
In fluid dynamics, aerodynamic potential flow codes or panel codes are used to determine the fluid velocity, and subsequently the pressure distribution, on an object. This may be a simple two-dimensional object, such as a circle or wing, or it may be a three-dimensional vehicle.
The convection–diffusion equation is a combination of the diffusion and convection (advection) equations, and describes physical phenomena where particles, energy, or other physical quantities are transferred inside a physical system due to two processes: diffusion and convection. Depending on context, the same equation can be called the advection–diffusion equation, drift–diffusion equation, or (generic) scalar transport equation.

In fluid dynamics, a cnoidal wave is a nonlinear and exact periodic wave solution of the Korteweg–de Vries equation. These solutions are in terms of the Jacobi elliptic function cn, which is why they are coined cnoidal waves. They are used to describe surface gravity waves of fairly long wavelength, as compared to the water depth.
Chapman–Enskog theory provides a framework in which equations of hydrodynamics for a gas can be derived from the Boltzmann equation. The technique justifies the otherwise phenomenological constitutive relations appearing in hydrodynamical descriptions such as the Navier–Stokes equations. In doing so, expressions for various transport coefficients such as thermal conductivity and viscosity are obtained in terms of molecular parameters. Thus, Chapman–Enskog theory constitutes an important step in the passage from a microscopic, particle-based description to a continuum hydrodynamical one.
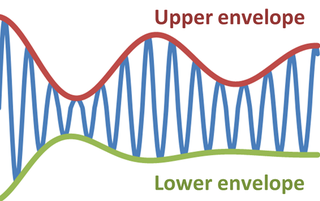
In physics and engineering, the envelope of an oscillating signal is a smooth curve outlining its extremes. The envelope thus generalizes the concept of a constant amplitude into an instantaneous amplitude. The figure illustrates a modulated sine wave varying between an upper envelope and a lower envelope. The envelope function may be a function of time, space, angle, or indeed of any variable.

In chaos theory and fluid dynamics, chaotic mixing is a process by which flow tracers develop into complex fractals under the action of a fluid flow. The flow is characterized by an exponential growth of fluid filaments. Even very simple flows, such as the blinking vortex, or finitely resolved wind fields can generate exceptionally complex patterns from initially simple tracer fields.
In fluid dynamics, a flow with periodic variations is known as pulsatile flow, or as Womersley flow. The flow profiles was first derived by John R. Womersley (1907–1958) in his work with blood flow in arteries. The cardiovascular system of chordate animals is a very good example where pulsatile flow is found, but pulsatile flow is also observed in engines and hydraulic systems, as a result of rotating mechanisms pumping the fluid.
In the science of fluid flow, Stokes' paradox is the phenomenon that there can be no creeping flow of a fluid around a disk in two dimensions; or, equivalently, the fact there is no non-trivial steady-state solution for the Stokes equations around an infinitely long cylinder. This is opposed to the 3-dimensional case, where Stokes' method provides a solution to the problem of flow around a sphere.
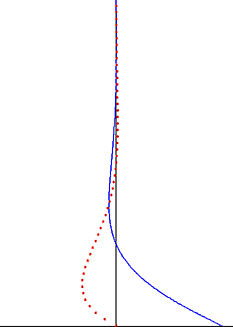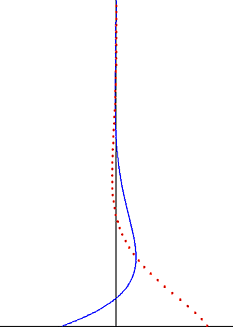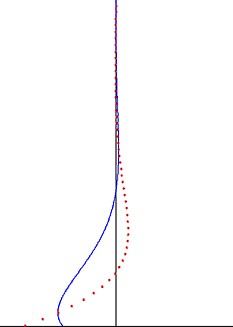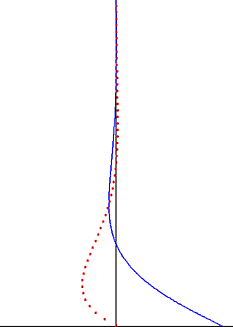
In fluid dynamics, Stokes problem also known as Stokes second problem or sometimes referred to as Stokes boundary layer or Oscillating boundary layer is a problem of determining the flow created by an oscillating solid surface, named after Sir George Stokes. This is considered one of the simplest unsteady problems that has an exact solution for the Navier-Stokes equations. In turbulent flow, this is still named a Stokes boundary layer, but now one has to rely on experiments, numerical simulations or approximate methods in order to obtain useful information on the flow.

Jan Jozef van Deemter was a Dutch physicist and engineer known for the Van Deemter equation in chromatography.
Alírio Rodrigues is a Portuguese chemical engineer. He is emeritus Professor of Chemical Engineering at Universidade do Porto and Director of the Laboratory of Separation and Reaction Engineering.


























