Related Research Articles

Mathematical optimization or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries.
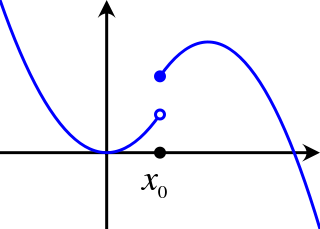
In mathematical analysis, semicontinuity is a property of extended real-valued functions that is weaker than continuity. An extended real-valued function is uppersemicontinuous at a point if, roughly speaking, the function values for arguments near are not much higher than
In mathematical analysis, in particular the subfields of convex analysis and optimization, a proper convex function is an extended real-valued convex function with a non-empty domain, that never takes on the value and also is not identically equal to

Pierre-Louis Lions is a French mathematician. He is known for a number of contributions to the fields of partial differential equations and the calculus of variations. He was a recipient of the 1994 Fields Medal and the 1991 Prize of the Philip Morris tobacco and cigarette company.
In convex analysis and the calculus of variations, both branches of mathematics, a pseudoconvex function is a function that behaves like a convex function with respect to finding its local minima, but need not actually be convex. Informally, a differentiable function is pseudoconvex if it is increasing in any direction where it has a positive directional derivative. The property must hold in all of the function domain, and not only for nearby points.

Convex analysis is the branch of mathematics devoted to the study of properties of convex functions and convex sets, often with applications in convex minimization, a subdomain of optimization theory.

In mathematics, subderivatives generalizes the derivative to convex functions which are not necessarily differentiable. The set of subderivatives at a point is called the subdifferential at that point. Subderivatives arise in convex analysis, the study of convex functions, often in connection to convex optimization.

In mathematics, the epigraph or supergraph of a function valued in the extended real numbers is the set

A set-valued function is a mathematical function that maps elements from one set, the domain of the function, to subsets of another set. Set-valued functions are used in a variety of mathematical fields, including optimization, control theory and game theory.

In mathematics, the hypograph or subgraph of a function is the set of points lying on or below its graph. A related definition is that of such a function's epigraph, which is the set of points on or above the function's graph.
Roger Jean-Baptiste Robert Wets is a "pioneer" in stochastic programming and a leader in variational analysis who publishes as Roger J-B Wets. His research, expositions, graduate students, and his collaboration with R. Tyrrell Rockafellar have had a profound influence on optimization theory, computations, and applications. Since 2009, Wets has been a distinguished research professor at the mathematics department of the University of California, Davis.

Ralph Tyrrell Rockafellar is an American mathematician and one of the leading scholars in optimization theory and related fields of analysis and combinatorics. He is the author of four major books including the landmark text "Convex Analysis" (1970), which has been cited more than 27,000 times according to Google Scholar and remains the standard reference on the subject, and "Variational Analysis" for which the authors received the Frederick W. Lanchester Prize from the Institute for Operations Research and the Management Sciences (INFORMS).
Convexity is an important topic in economics. In the Arrow–Debreu model of general economic equilibrium, agents have convex budget sets and convex preferences: At equilibrium prices, the budget hyperplane supports the best attainable indifference curve. The profit function is the convex conjugate of the cost function. Convex analysis is the standard tool for analyzing textbook economics. Non‑convex phenomena in economics have been studied with nonsmooth analysis, which generalizes convex analysis.
Ivar I. Ekeland is a French mathematician of Norwegian descent. Ekeland has written influential monographs and textbooks on nonlinear functional analysis, the calculus of variations, and mathematical economics, as well as popular books on mathematics, which have been published in French, English, and other languages. Ekeland is known as the author of Ekeland's variational principle and for his use of the Shapley–Folkman lemma in optimization theory. He has contributed to the periodic solutions of Hamiltonian systems and particularly to the theory of Kreĭn indices for linear systems. Ekeland is cited in the credits of Steven Spielberg's 1993 movie Jurassic Park as an inspiration of the fictional chaos theory specialist Ian Malcom appearing in Michael Crichton's 1990 novel Jurassic Park.
In convex analysis, a branch of mathematics, the effective domain extends of the domain of a function defined for functions that take values in the extended real number line

Jean Jacques Moreau was a French mathematician and mechanician. He normally published under the name J. J. Moreau.
Frank "Francis" H. Clarke is a Canadian and French mathematician.
In mathematics, the Clarke generalized derivatives are types generalized of derivatives that allow for the differentiation of nonsmooth functions. The Clarke derivatives were introduced by Francis Clarke in 1975.
References
- Rockafellar, R. Tyrrell; Wets, Roger J.-B. (26 June 2009). Variational Analysis. Grundlehren der mathematischen Wissenschaften. Vol. 317. Berlin New York: Springer Science & Business Media. ISBN 9783642024313. OCLC 883392544.