
Area is the measure of a region's size on a surface. The area of a plane region or plane area refers to the area of a shape or planar lamina, while surface area refers to the area of an open surface or the boundary of a three-dimensional object. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat. It is the two-dimensional analogue of the length of a curve or the volume of a solid . Two different regions may have the same area ; by synecdoche, "area" sometimes is used to refer to the region, as in a "polygonal area".

A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. The distance between any point of the circle and the centre is called the radius. Usually, the radius is required to be a positive number. A circle with is a degenerate case. This article is about circles in Euclidean geometry, and, in particular, the Euclidean plane, except where otherwise noted.

In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Expressed algebraically, for quantities and with ,
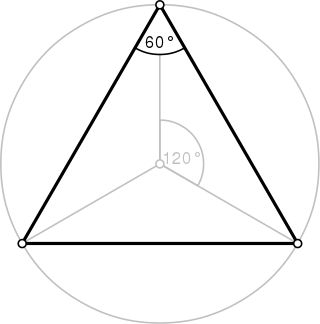
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices A, B, and C is denoted .

In geometry, a hexagon is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°.

In geometry, an equilateral triangle is a triangle in which all three sides have the same length. In the familiar Euclidean geometry, an equilateral triangle is also equiangular; that is, all three internal angles are also congruent to each other and are each 60°. It is also a regular polygon, so it is also referred to as a regular triangle.
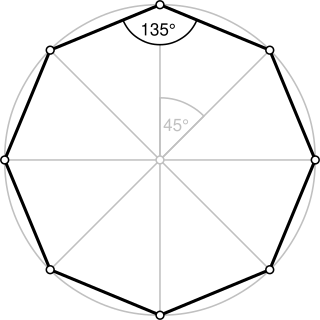
In geometry, an octagon is an eight-sided polygon or 8-gon.

In geometry, an isosceles triangle is a triangle that has two sides of equal length. Sometimes it is specified as having exactly two sides of equal length, and sometimes as having at least two sides of equal length, the latter version thus including the equilateral triangle as a special case. Examples of isosceles triangles include the isosceles right triangle, the golden triangle, and the faces of bipyramids and certain Catalan solids.

In geometry, a decagon is a ten-sided polygon or 10-gon. The total sum of the interior angles of a simple decagon is 1440°.
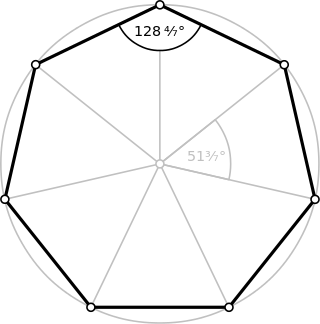
In geometry, a heptagon or septagon is a seven-sided polygon or 7-gon.

A Reuleaux triangle[ʁœlo] is a curved triangle with constant width, the simplest and best known curve of constant width other than the circle. It is formed from the intersection of three circular disks, each having its center on the boundary of the other two. Constant width means that the separation of every two parallel supporting lines is the same, independent of their orientation. Because its width is constant, the Reuleaux triangle is one answer to the question "Other than a circle, what shape can a manhole cover be made so that it cannot fall down through the hole?"
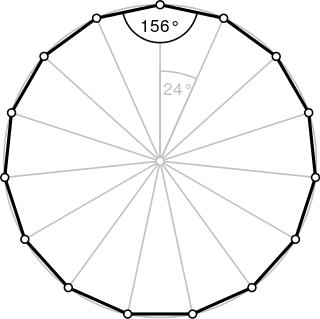
In geometry, a pentadecagon or pentakaidecagon or 15-gon is a fifteen-sided polygon.

A mandorla is an almond-shaped aureola, i.e. a frame that surrounds the totality of an iconographic figure. It is usually synonymous with vesica, a lens shape. Mandorlas often surround the figures of Jesus Christ and the Virgin Mary in traditional Christian iconography. It is distinguished from a halo in that it encircles the entire body and not just the head. It is commonly used to frame the figure of Christ in Majesty in early medieval and Romanesque art, as well as Byzantine art of the same periods. It is the shape generally used for mediaeval ecclesiastical seals, secular seals generally being round.

In 2-dimensional geometry, a lens is a convex region bounded by two circular arcs joined to each other at their endpoints. In order for this shape to be convex, both arcs must bow outwards (convex-convex). This shape can be formed as the intersection of two circular disks. It can also be formed as the union of two circular segments, joined along a common chord.

A special right triangle is a right triangle with some regular feature that makes calculations on the triangle easier, or for which simple formulas exist. For example, a right triangle may have angles that form simple relationships, such as 45°–45°–90°. This is called an "angle-based" right triangle. A "side-based" right triangle is one in which the lengths of the sides form ratios of whole numbers, such as 3 : 4 : 5, or of other special numbers such as the golden ratio. Knowing the relationships of the angles or ratios of sides of these special right triangles allows one to quickly calculate various lengths in geometric problems without resorting to more advanced methods.

In hyperbolic geometry an ideal triangle is a hyperbolic triangle whose three vertices all are ideal points. Ideal triangles are also sometimes called triply asymptotic triangles or trebly asymptotic triangles. The vertices are sometimes called ideal vertices. All ideal triangles are congruent.

The square root of 3 is the positive real number that, when multiplied by itself, gives the number 3. It is denoted mathematically as or . It is more precisely called the principal square root of 3 to distinguish it from the negative number with the same property. The square root of 3 is an irrational number. It is also known as Theodorus' constant, after Theodorus of Cyrene, who proved its irrationality.
In geometry, a pentagon is any five-sided polygon or 5-gon. The sum of the internal angles in a simple pentagon is 540°.
In geometry, the mean line segment length is the average length of a line segment connecting two points chosen uniformly at random in a given shape. In other words, it is the expected Euclidean distance between two random points, where each point in the shape is equally likely to be chosen.




























