Related Research Articles

In graph theory, the shortest path problem is the problem of finding a path between two vertices in a graph such that the sum of the weights of its constituent edges is minimized.
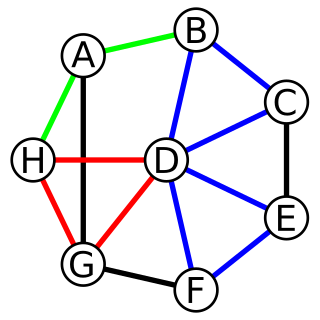
In graph theory, a cycle in a graph is a non-empty trail in which only the first and last vertices are equal. A directed cycle in a directed graph is a non-empty directed trail in which only the first and last vertices are equal.
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational geometry. While modern computational geometry is a recent development, it is one of the oldest fields of computing with a history stretching back to antiquity.
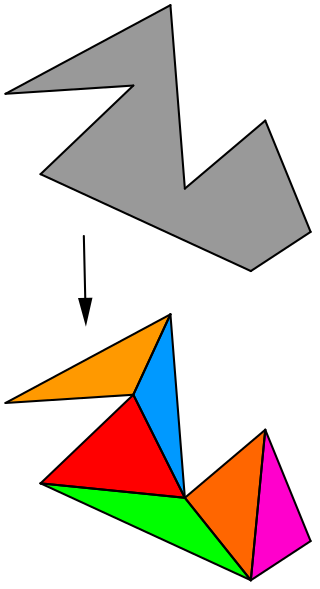
In computational geometry, polygon triangulation is the partition of a polygonal area P into a set of triangles, i.e., finding a set of triangles with pairwise non-intersecting interiors whose union is P.

In geometry, an arrangement of lines is the subdivision of the plane formed by a collection of lines. Bounds on the complexity of arrangements have been studied in discrete geometry, and computational geometers have found algorithms for the efficient construction of arrangements.

A Euclidean minimum spanning tree of a finite set of points in the Euclidean plane or higher-dimensional Euclidean space connects the points by a system of line segments with the points as endpoints, minimizing the total length of the segments. In it, any two points can reach each other along a path through the line segments. It can be found as the minimum spanning tree of a complete graph with the points as vertices and the Euclidean distances between points as edge weights.

In geometry, a bitangent to a curve C is a line L that touches C in two distinct points P and Q and that has the same direction as C at these points. That is, L is a tangent line at P and at Q.
Motion planning, also path planning is a computational problem to find a sequence of valid configurations that moves the object from the source to destination. The term is used in computational geometry, computer animation, robotics and computer games.
In geometry, visibility is a mathematical abstraction of the real-life notion of visibility.

In Euclidean plane geometry, a pseudotriangle (pseudo-triangle) is the simply connected subset of the plane that lies between any three mutually tangent convex sets. A pseudotriangulation (pseudo-triangulations) is a partition of a region of the plane into pseudotriangles, and a pointed pseudotriangulation is a pseudotriangulation in which at each vertex the incident edges span an angle of less than π.

The Euclidean shortest path problem is a problem in computational geometry: given a set of polyhedral obstacles in a Euclidean space, and two points, find the shortest path between the points that does not intersect any of the obstacles.

In computational geometry, the visibility polygon or visibility region for a point p in the plane among obstacles is the possibly unbounded polygonal region of all points of the plane visible from p. The visibility polygon can also be defined for visibility from a segment, or a polygon. Visibility polygons are useful in robotics, video games, and in various optimization problems such as the facility location problem and the art gallery problem.

In geometry, a polygonal chain is a connected series of line segments. More formally, a polygonal chain is a curve specified by a sequence of points called its vertices. The curve itself consists of the line segments connecting the consecutive vertices.

The nearest neighbor graph (NNG) is a directed graph defined for a set of points in a metric space, such as the Euclidean distance in the plane. The NNG has a vertex for each point, and a directed edge from p to q whenever q is a nearest neighbor of p, a point whose distance from p is minimum among all the given points other than p itself.

In computational geometry, the method of rotating calipers is an algorithm design technique that can be used to solve optimization problems including finding the width or diameter of a set of points.

In graph algorithms, the widest path problem is the problem of finding a path between two designated vertices in a weighted graph, maximizing the weight of the minimum-weight edge in the path. The widest path problem is also known as the maximum capacity path problem. It is possible to adapt most shortest path algorithms to compute widest paths, by modifying them to use the bottleneck distance instead of path length. However, in many cases even faster algorithms are possible.
John E. Hershberger is an American computer scientist and software professional, a principal engineer at Mentor Graphics Corporation since 1993. He is known for his research in computational geometry and algorithm engineering.
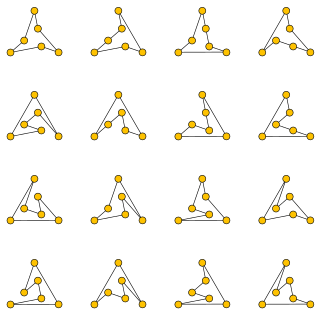
In computational geometry, a polygonalization of a finite set of points in the Euclidean plane is a simple polygon with the given points as its vertices. A polygonalization may also be called a polygonization, simple polygonalization, Hamiltonian polygon, non-crossing Hamiltonian cycle, or crossing-free straight-edge spanning cycle.
References
- de Berg, Mark; van Kreveld, Marc; Overmars, Mark; Schwarzkopf, Otfried (2000), "Chapter 15: Visibility Graphs", Computational Geometry (2nd ed.), Springer-Verlag, pp. 307–317, ISBN 978-3-540-65620-3 .
- Lozano-Pérez, Tomás; Wesley, Michael A. (1979), "An algorithm for planning collision-free paths among polyhedral obstacles", Communications of the ACM, 22 (10): 560–570, doi: 10.1145/359156.359164 , S2CID 17397594 .