
In probability theory and statistics, the exponential distribution or negative exponential distribution is the probability distribution of the time between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate. It is a particular case of the gamma distribution. It is the continuous analogue of the geometric distribution, and it has the key property of being memoryless. In addition to being used for the analysis of Poisson point processes it is found in various other contexts.

The Pareto distribution, named after the Italian civil engineer, economist, and sociologist Vilfredo Pareto, is a power-law probability distribution that is used in description of social, quality control, scientific, geophysical, actuarial, and many other types of observable phenomena; the principle originally applied to describing the distribution of wealth in a society, fitting the trend that a large portion of wealth is held by a small fraction of the population. The Pareto principle or "80-20 rule" stating that 80% of outcomes are due to 20% of causes was named in honour of Pareto, but the concepts are distinct, and only Pareto distributions with shape value of log45 ≈ 1.16 precisely reflect it. Empirical observation has shown that this 80-20 distribution fits a wide range of cases, including natural phenomena and human activities.

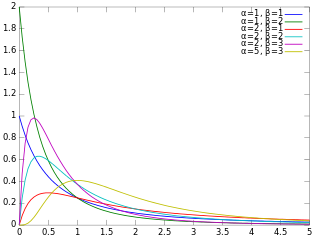
In probability theory and statistics, the gamma distribution is a two-parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-squared distribution are special cases of the gamma distribution. There are two equivalent parameterizations in common use:
- With a shape parameter and a scale parameter .
- With a shape parameter and an inverse scale parameter , called a rate parameter.

In probability theory, a distribution is said to be stable if a linear combination of two independent random variables with this distribution has the same distribution, up to location and scale parameters. A random variable is said to be stable if its distribution is stable. The stable distribution family is also sometimes referred to as the Lévy alpha-stable distribution, after Paul Lévy, the first mathematician to have studied it.
In probability theory and statistics, the generalized extreme value (GEV) distribution is a family of continuous probability distributions developed within extreme value theory to combine the Gumbel, Fréchet and Weibull families also known as type I, II and III extreme value distributions. By the extreme value theorem the GEV distribution is the only possible limit distribution of properly normalized maxima of a sequence of independent and identically distributed random variables. Note that a limit distribution needs to exist, which requires regularity conditions on the tail of the distribution. Despite this, the GEV distribution is often used as an approximation to model the maxima of long (finite) sequences of random variables.

In probability and statistics, the Kumaraswamy's double bounded distribution is a family of continuous probability distributions defined on the interval (0,1). It is similar to the Beta distribution, but much simpler to use especially in simulation studies since its probability density function, cumulative distribution function and quantile functions can be expressed in closed form. This distribution was originally proposed by Poondi Kumaraswamy for variables that are lower and upper bounded with a zero-inflation. This was extended to inflations at both extremes [0,1] in later work with S. G. Fletcher.
In physics, precisely in the study of the theory of general relativity and many alternatives to it, the post-Newtonian formalism is a calculational tool that expresses Einstein's (nonlinear) equations of gravity in terms of the lowest-order deviations from Newton's law of universal gravitation. This allows approximations to Einstein's equations to be made in the case of weak fields. Higher-order terms can be added to increase accuracy, but for strong fields, it may be preferable to solve the complete equations numerically. Some of these post-Newtonian approximations are expansions in a small parameter, which is the ratio of the velocity of the matter forming the gravitational field to the speed of light, which in this case is better called the speed of gravity. In the limit, when the fundamental speed of gravity becomes infinite, the post-Newtonian expansion reduces to Newton's law of gravity.
In probability theory and statistics, the beta prime distribution is an absolutely continuous probability distribution. If has a beta distribution, then the odds has a beta prime distribution.
The normal-inverse Gaussian distribution is a continuous probability distribution that is defined as the normal variance-mean mixture where the mixing density is the inverse Gaussian distribution. The NIG distribution was noted by Blaesild in 1977 as a subclass of the generalised hyperbolic distribution discovered by Ole Barndorff-Nielsen. In the next year Barndorff-Nielsen published the NIG in another paper. It was introduced in the mathematical finance literature in 1997.
Expected shortfall (ES) is a risk measure—a concept used in the field of financial risk measurement to evaluate the market risk or credit risk of a portfolio. The "expected shortfall at q% level" is the expected return on the portfolio in the worst of cases. ES is an alternative to value at risk that is more sensitive to the shape of the tail of the loss distribution.
A ratio distribution is a probability distribution constructed as the distribution of the ratio of random variables having two other known distributions. Given two random variables X and Y, the distribution of the random variable Z that is formed as the ratio Z = X/Y is a ratio distribution.
Tail value at risk (TVaR), also known as tail conditional expectation (TCE) or conditional tail expectation (CTE), is a risk measure associated with the more general value at risk. It quantifies the expected value of the loss given that an event outside a given probability level has occurred.
The Birnbaum–Saunders distribution, also known as the fatigue life distribution, is a probability distribution used extensively in reliability applications to model failure times. There are several alternative formulations of this distribution in the literature. It is named after Z. W. Birnbaum and S. C. Saunders.

The shifted log-logistic distribution is a probability distribution also known as the generalized log-logistic or the three-parameter log-logistic distribution. It has also been called the generalized logistic distribution, but this conflicts with other uses of the term: see generalized logistic distribution.

In probability theory and statistics, the skew normal distribution is a continuous probability distribution that generalises the normal distribution to allow for non-zero skewness.

In mathematics, Montgomery's pair correlation conjecture is a conjecture made by Hugh Montgomery (1973) that the pair correlation between pairs of zeros of the Riemann zeta function is
In probability and statistics, the generalized K-distribution is a three-parameter family of continuous probability distributions. The distribution arises by compounding two gamma distributions. In each case, a re-parametrization of the usual form of the family of gamma distributions is used, such that the parameters are:
Hypertabastic survival models were introduced in 2007 by Mohammad Tabatabai, Zoran Bursac, David Williams, and Karan Singh. This distribution can be used to analyze time-to-event data in biomedical and public health areas and normally called survival analysis. In engineering, the time-to event analysis is referred to as reliability theory and in business and economics it is called duration analysis. Other fields may use different names for the same analysis. These survival models are applicable in many fields such as biomedical, behavioral science, social science, statistics, medicine, bioinformatics, medicalinformatics, data science especially in machine learning, computational biology, business economics, engineering, and commercial entities. They not only look at the time to event, but whether or not the event occurred. These time-to-event models can be applied in a variety of applications for instance, time after diagnosis of cancer until death, comparison of individualized treatment with standard care in cancer research, time until an individual defaults on loans, relapsed time for drug and smoking cessation, time until property sold after being put on the market, time until an individual upgrades to a new phone, time until job relocation, time until bones receive microscopic fractures when undergoing different stress levels, time from marriage until divorce, time until infection due to catheter, and time from bridge completion until first repair.

The Kaniadakis Weibull distribution is a probability distribution arising as a generalization of the Weibull distribution. It is one example of a Kaniadakis κ-distribution. The κ-Weibull distribution has been adopted successfully for describing a wide variety of complex systems in seismology, economy, epidemiology, among many others.

The Kaniadakis Generalized Gamma distribution is a four-parameter family of continuous statistical distributions, supported on a semi-infinite interval [0,∞), which arising from the Kaniadakis statistics. It is one example of a Kaniadakis distribution. The κ-Gamma is a deformation of the Generalized Gamma distribution.




































