This article needs additional citations for verification .(September 2014) (Learn how and when to remove this template message) |
In mathematics, the term weak inverse is used with several meanings.
This article needs additional citations for verification .(September 2014) (Learn how and when to remove this template message) |
In mathematics, the term weak inverse is used with several meanings.
In the theory of semigroups, a weak inverse of an element x in a semigroup (S, •) is an element y such that y • x • y = y. If every element has a weak inverse, the semigroup is called an E-inversive or E-dense semigroup. An E-inversive semigroup may equivalently be defined by requiring that for every element x ∈ S, there exists y ∈ S such that x • y and y • x are idempotents. [1]
An element x of S for which there is an element y of S such that x • y • x = x is called regular. A regular semigroup is a semigroup in which every element is regular. This is a stronger notion than weak inverse. Every regular semigroup is E-inversive, but not vice versa. [1]
If every element x in S has a unique inverse y in S in the sense that x • y • x = x and y • x • y = y then S is called an inverse semigroup.
In category theory, a weak inverse of an object A in a monoidal category C with monoidal product ⊗ and unit object I is an object B such that both A ⊗ B and B ⊗ A are isomorphic to the unit object I of C. A monoidal category in which every morphism is invertible and every object has a weak inverse is called a 2-group.
In algebra, a homomorphism is a structure-preserving map between two algebraic structures of the same type. The word homomorphism comes from the ancient Greek language: ὁμός (homos) meaning "same" and μορφή (morphe) meaning "form" or "shape". However, the word was apparently introduced to mathematics due to a (mis)translation of German ähnlich meaning "similar" to ὁμός meaning "same". The term "homomorphism" appeared as early as 1892 ; it was attributed to the German mathematician Felix Klein (1849–1925).
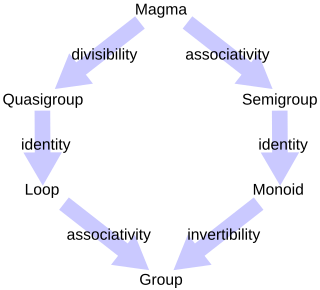
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element.
In mathematics, a partial function is a binary relation over two sets that associates to every element of the first set at most one element of the second set. It generalizes the concept of a function by not requiring every element of the first set to be associated to at least one element of the second set. Consequently, the domain of definition of a partial function can be a proper subset of its domain, contrary to a function for which the two sets always coincide.

In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation.
In abstract algebra, the idea of an inverse element generalises the concepts of negation and reciprocation. The intuition is of an element that can 'undo' the effect of combination with another given element. While the precise definition of an inverse element varies depending on the algebraic structure involved, these definitions coincide in a group.
In mathematics, more specifically in abstract algebra and universal algebra, an algebraic structure consists of a set A, a collection of operations on A of finite arity, and a finite set of identities, known as axioms, that these operations must satisfy. Some algebraic structures also involve another set.

In abstract algebra, a magma is a basic kind of algebraic structure. Specifically, a magma consists of a set equipped with a single binary operation. The binary operation must be closed by definition but no other properties are imposed.
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property. The representation theory of a Hopf algebra is particularly nice, since the existence of compatible comultiplication, counit, and antipode allows for the construction of tensor products of representations, trivial representations, and dual representations.
In mathematics, a monoidal category is a category equipped with a bifunctor
In mathematics, localization of a category consists of adding to a category inverse morphisms for some collection of morphisms, constraining them to become isomorphisms. This is formally similar to the process of localization of a ring; it in general makes objects isomorphic that were not so before. In homotopy theory, for example, there are many examples of mappings that are invertible up to homotopy; and so large classes of homotopy equivalent spaces. Calculus of fractions is another name for working in a localized category.
In universal algebra, a variety of algebras or equational class is the class of all algebraic structures of a given signature satisfying a given set of identities. For example, the groups form a variety of algebras, as do the abelian groups, the rings, the monoids etc. According to Birkhoff's theorem, a class of algebraic structures of the same signature is a variety if and only if it is closed under the taking of homomorphic images, subalgebras and (direct) products. In the context of category theory, a variety of algebras, together with its homomorphisms, forms a category; these are usually called finitary algebraic categories.
In mathematics, the bicyclic semigroup is an algebraic object important for the structure theory of semigroups. Although it is in fact a monoid, it is usually referred to as simply a semigroup. It is perhaps most easily understood as the syntactic monoid describing the Dyck language of balanced pairs of parentheses. Thus, it finds common applications in combinatorics, such as describing binary trees and associative algebras.

In group theory, an inverse semigroupS is a semigroup in which every element x in S has a unique inversey in S in the sense that x = xyx and y = yxy, i.e. a regular semigroup in which every element has a unique inverse. Inverse semigroups appear in a range of contexts; for example, they can be employed in the study of partial symmetries.
This is a glossary of properties and concepts in category theory in mathematics.
In category theory, a branch of mathematics, a symmetric monoidal category is a monoidal category such that the tensor product is symmetric. One of the prototypical examples of a symmetric monoidal category is the category of vector spaces over some fixed field k, using the ordinary tensor product of vector spaces.
In abstract algebra, a semiheap is an algebraic structure consisting of a non-empty set H with a ternary operation denoted that satisfies a modified associativity property:
In mathematics, a regular semigroup is a semigroup S in which every element is regular, i.e., for each element a, there exists an element x such that axa = a. Regular semigroups are one of the most-studied classes of semigroups, and their structure is particularly amenable to study via Green's relations.
In mathematics, a 2-group, or 2-dimensional higher group, is a certain combination of group and groupoid. The 2-groups are part of a larger hierarchy of n-groups. In some of the literature, 2-groups are also called gr-categories or groupal groupoids.
In mathematics, particularly in abstract algebra, a semigroup with involution or a *-semigroup is a semigroup equipped with an involutive anti-automorphism, which—roughly speaking—brings it closer to a group because this involution, considered as unary operator, exhibits certain fundamental properties of the operation of taking the inverse in a group: uniqueness, double application "cancelling itself out", and the same interaction law with the binary operation as in the case of the group inverse. It is thus not a surprise that any group is a semigroup with involution. However, there are significant natural examples of semigroups with involution that are not groups.
In abstract algebra, an E-dense semigroup is a semigroup in which every element a has at least one weak inversex, meaning that xax = x. The notion of weak inverse is weaker than the notion of inverse used in a regular semigroup.
| This category theory-related article is a stub. You can help Wikipedia by expanding it. |
| This abstract algebra-related article is a stub. You can help Wikipedia by expanding it. |