Zachary's karate club is a social network of a university karate club, described in the paper "An Information Flow Model for Conflict and Fission in Small Groups" by Wayne W. Zachary. The network became a popular example of community structure in networks after its use by Michelle Girvan and Mark Newman in 2002. [1]
A social network of a karate club was studied by Wayne W. Zachary for a period of three years from 1970 to 1972. [2] The network captures 34 members of a karate club, documenting links between pairs of members who interacted outside the club. During the study a conflict arose between the administrator "John A" and instructor "Mr. Hi" (pseudonyms), which led to the split of the club into two. Half of the members formed a new club around Mr. Hi; members from the other part found a new instructor or gave up karate. Based on collected data Zachary correctly assigned all but one member of the club to the groups they actually joined after the split.
Before the split each side tried to recruit adherents of the other party. Thus, communication flow had a special importance and the initial group would likely split at the "borders" of the network. Zachary used the maximum flow – minimum cut Ford–Fulkerson algorithm from “source” Mr. Hi to “sink” John A: the cut closest to Mr. Hi that cuts saturated edges divides the network into the two factions. Zachary correctly predicted each member's decision except member #9, who went with Mr. Hi instead of John A.
The standard 78-edge network data set for Zachary's karate club is publicly available on the internet. [3] The data can be summarized as list of integer pairs. Each integer represents one karate club member and a pair indicates the two members interacted. The data set is summarized below and also in the adjoining image. Node 1 stands for the instructor, node 34 for the club administrator / president.
[2 1] [3 1] [3 2] [4 1] [4 2] [4 3] [5 1] [6 1] [7 1] [7 5] [7 6] [8 1] [8 2] [8 3] [8 4] [9 1] [9 3] [10 3] [11 1] [11 5] [11 6] [12 1] [13 1] [13 4] [14 1] [14 2] [14 3] [14 4] [17 6] [17 7] [18 1] [18 2] [20 1] [20 2] [22 1] [22 2] [26 24] [26 25] [28 3] [28 24] [28 25] [29 3] [30 24] [30 27] [31 2] [31 9] [32 1] [32 25] [32 26] [32 29] [33 3] [33 9] [33 15] [33 16] [33 19] [33 21] [33 23] [33 24] [33 30] [33 31] [33 32] [34 9] [34 10] [34 14] [34 15] [34 16] [34 19] [34 20] [34 21] [34 23] [34 24] [34 27] [34 28] [34 29] [34 30] [34 31] [34 32] [34 33]
Although this version of the network is considered standard, the connection between nodes 34 and 23 is ambiguously reported in Zachary's original paper. A 77-edge version, which omits this edge, is also publicly available. [4]
Zachary Karate Club Club is a honorific group [5] that awards membership in the group, along with a traveling trophy, to a scientist who is the first to use Zachary's Karate Club as an example at a conference on networks. The first scientist to be awarded was Cristopher Moore [6] in 2013, at a conference at the Santa Fe Institute.
Network, networking and networked may refer to:
A minimum spanning tree (MST) or minimum weight spanning tree is a subset of the edges of a connected, edge-weighted undirected graph that connects all the vertices together, without any cycles and with the minimum possible total edge weight. That is, it is a spanning tree whose sum of edge weights is as small as possible. More generally, any edge-weighted undirected graph has a minimum spanning forest, which is a union of the minimum spanning trees for its connected components.
Graph drawing is an area of mathematics and computer science combining methods from geometric graph theory and information visualization to derive two-dimensional depictions of graphs arising from applications such as social network analysis, cartography, linguistics, and bioinformatics.
In graph theory, a flow network is a directed graph where each edge has a capacity and each edge receives a flow. The amount of flow on an edge cannot exceed the capacity of the edge. Often in operations research, a directed graph is called a network, the vertices are called nodes and the edges are called arcs. A flow must satisfy the restriction that the amount of flow into a node equals the amount of flow out of it, unless it is a source, which has only outgoing flow, or sink, which has only incoming flow. A network can be used to model traffic in a computer network, circulation with demands, fluids in pipes, currents in an electrical circuit, or anything similar in which something travels through a network of nodes.
In mathematics, computer science and network science, network theory is a part of graph theory. It defines networks as graphs where the nodes or edges possess attributes. Network theory analyses these networks over the symmetric relations or asymmetric relations between their (discrete) components.
In mathematics, and, in particular, in graph theory, a rooted graph is a graph in which one vertex has been distinguished as the root. Both directed and undirected versions of rooted graphs have been studied, and there are also variant definitions that allow multiple roots.
In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements that need to be removed to separate the remaining nodes into two or more isolated subgraphs. It is closely related to the theory of network flow problems. The connectivity of a graph is an important measure of its resilience as a network.
Neuroinformatics is the field that combines informatics and neuroscience. Neuroinformatics is related with neuroscience data and information processing by artificial neural networks. There are three main directions where neuroinformatics has to be applied:
The Organization for Human Brain Mapping (OHBM) is an organization of scientists with the main aim of organizing an annual meeting.
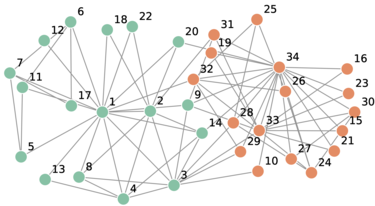
In the study of complex networks, a network is said to have community structure if the nodes of the network can be easily grouped into sets of nodes such that each set of nodes is densely connected internally. In the particular case of non-overlapping community finding, this implies that the network divides naturally into groups of nodes with dense connections internally and sparser connections between groups. But overlapping communities are also allowed. The more general definition is based on the principle that pairs of nodes are more likely to be connected if they are both members of the same community(ies), and less likely to be connected if they do not share communities. A related but different problem is community search, where the goal is to find a community that a certain vertex belongs to.
The Girvan–Newman algorithm is a hierarchical method used to detect communities in complex systems.
In network science, a gradient network is a directed subnetwork of an undirected "substrate" network where each node has an associated scalar potential and one out-link that points to the node with the smallest potential in its neighborhood, defined as the union of itself and its neighbors on the substrate network.
Mark Newman is an English–American physicist and Anatol Rapoport Distinguished University Professor of Physics at the University of Michigan, as well as an external faculty member of the Santa Fe Institute. He is known for his fundamental contributions to the fields of complex networks and complex systems, for which he was awarded the 2014 Lagrange Prize.
Modularity is a measure of the structure of networks or graphs which measures the strength of division of a network into modules. Networks with high modularity have dense connections between the nodes within modules but sparse connections between nodes in different modules. Modularity is often used in optimization methods for detecting community structure in networks. Biological networks, including animal brains, exhibit a high degree of modularity. However, modularity maximization is not statistically consistent, and finds communities in its own null model, i.e. fully random graphs, and therefore it cannot be used to find statistically significant community structures in empirical networks. Furthermore, it has been shown that modularity suffers a resolution limit and, therefore, it is unable to detect small communities.
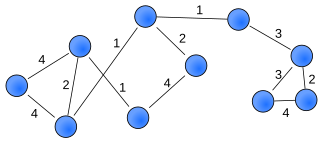
A weighted network is a network where the ties among nodes have weights assigned to them. A network is a system whose elements are somehow connected. The elements of a system are represented as nodes and the connections among interacting elements are known as ties, edges, arcs, or links. The nodes might be neurons, individuals, groups, organisations, airports, or even countries, whereas ties can take the form of friendship, communication, collaboration, alliance, flow, or trade, to name a few.
Cristopher David Moore, known as Cris Moore, is an American computer scientist, mathematician, and physicist. He is resident faculty at the Santa Fe Institute, and was formerly a full professor at the University of New Mexico.
Bipartite network projection is an extensively used method for compressing information about bipartite networks. Since the one-mode projection is always less informative than the original bipartite graph, an appropriate method for weighting network connections is often required. Optimal weighting methods reflect the nature of the specific network, conform to the designer's objectives and aim at minimizing information loss.
The Louvain method for community detection is a method to extract non-overlapping communities from large networks created by Blondel et al. from the University of Louvain. The method is a greedy optimization method that appears to run in time where is the number of nodes in the network.
The stochastic block model is a generative model for random graphs. This model tends to produce graphs containing communities, subsets of nodes characterized by being connected with one another with particular edge densities. For example, edges may be more common within communities than between communities. Its mathematical formulation has been firstly introduced in 1983 in the field of social network by Paul W. Holland et al. The stochastic block model is important in statistics, machine learning, and network science, where it serves as a useful benchmark for the task of recovering community structure in graph data.
Aaron Clauset is an American computer scientist who works in the areas of Network Science, Machine Learning, and Complex Systems. He is currently a professor of computer science at the University of Colorado Boulder and is external faculty at the Santa Fe Institute.