Abramowitz and Stegun

Last updated

Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables
Handbook of Mathematical Functions, by Abramowitz and Stegun, cover.jpg
Cover of the ninth printing, 1970
Author Milton Abramowitz and Irene Stegun
CountryUnited States
LanguageEnglish
Genre Math
Publisher United States Department of Commerce, National Bureau of Standards (NBS)
Publication date
1964
ISBN 0-486-61272-4
OCLC 18003605

Abramowitz and Stegun (AS) is the informal name of a 1964 mathematical reference work edited by Milton Abramowitz and Irene Stegun of the United States National Bureau of Standards (NBS), now the National Institute of Standards and Technology (NIST). Its full title is Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. A digital successor to the Handbook was released as the "Digital Library of Mathematical Functions" (DLMF) on 11 May 2010, along with a printed version, the NIST Handbook of Mathematical Functions , published by Cambridge University Press. [1]

Contents

Overview

Since it was first published in 1964, the 1046 page Handbook has been one of the most comprehensive sources of information on special functions, containing definitions, identities, approximations, plots, and tables of values of numerous functions used in virtually all fields of applied mathematics. [2] [3] [4] The notation used in the Handbook is the de facto standard for much of applied mathematics today.

At the time of its publication, the Handbook was an essential resource for practitioners. Nowadays, computer algebra systems have replaced the function tables, but the Handbook remains an important reference source. The foreword discusses a meeting in 1954 in which it was agreed that "the advent of high-speed computing equipment changed the task of table making but definitely did not remove the need for tables".

More than 1,000 pages long, the Handbook of Mathematical Functions was first published in 1964 and reprinted many times, with yet another reprint in 1999. Its influence on science and engineering is evidenced by its popularity. In fact, when New Scientist magazine recently asked some of the world's leading scientists what single book they would want if stranded on a desert island, one distinguished British physicist [5] said he would take the Handbook. The Handbook is likely the most widely distributed and most cited NIST technical publication of all time. Government sales exceed 150,000 copies, and an estimated three times as many have been reprinted and sold by commercial publishers since 1965. During the mid-1990s, the book was cited every 1.5 hours of each working day. And its influence will persist as it is currently being updated in digital format by NIST.

—  NIST [6]
Page 97 showing part of a table of common logarithms Abramowitz&Stegun.page97.agr.jpg
Page 97 showing part of a table of common logarithms

The chapters are:

  1. Mathematical Constants
  2. Physical Constants and Conversion Factors
  3. Elementary Analytical Methods
  4. Elementary Transcendental Functions
  5. Exponential Integral and Related Functions
  6. Gamma Function and Related Functions
  7. Error Function and Fresnel Integrals
  8. Legendre Functions
  9. Bessel Functions of Integral Order
  10. Bessel Functions of Fractional Order
  11. Integrals of Bessel Functions
  12. Struve Functions and Related Functions
  13. Confluent Hypergeometric Functions
  14. Coulomb Wave Functions
  15. Hypergeometric Functions
  16. Jacobian Elliptic Functions and Theta Functions
  17. Elliptic Integrals
  18. Weierstrass Elliptic and Related Functions
  19. Parabolic Cylinder Functions
  20. Mathieu Functions
  21. Spheroidal Wave Functions
  22. Orthogonal Polynomials
  23. Bernoulli and Euler Polynomials, Riemann Zeta Function
  24. Combinatorial Analysis
  25. Numerical Interpolation, Differentiation, and Integration
  26. Probability Functions
  27. Miscellaneous Functions
  28. Scales of Notation
  29. Laplace Transforms

Editions

Because the Handbook is the work of U.S. federal government employees acting in their official capacity, it is not protected by copyright in the United States. While it could be ordered from the Government Printing Office, it has also been reprinted by commercial publishers, most notably Dover Publications ( ISBN   0-486-61272-4), and can be legally viewed on and downloaded from the web.

While there was only one edition of the work, it went through many print runs including a growing number of corrections.

Original NBS edition:

Reprint edition by Dover Publications:

Michael Danos and Johann Rafelski edited the Pocketbook of Mathematical Functions, published by Verlag Harri Deutsch in 1984. [14] [15] The book is an abridged version of Abramowitz's and Stegun's Handbook, retaining most of the formulas (except for the first and the two last original chapters, which were dropped), but reducing the numerical tables to a minimum, [14] which, by this time, could be easily calculated with scientific pocket calculators. [15] The references were removed as well. [15] Most known errata were incorporated, the physical constants updated and the now-first chapter saw some slight enlargement compared to the former second chapter. [15] The numbering of formulas was kept for easier cross-reference. [15]

A digital successor to the Handbook, long under development at NIST, was released as the “Digital Library of Mathematical Functions” (DLMF) on 11 May 2010, along with a printed version, the NIST Handbook of Mathematical Functions , published by Cambridge University Press. [1]

See also

Notes

  1. 1 2 3 4 5 6 7 Up to the tenth printing of the original NBS edition in December 1972, corrections were incorporated on pages 2–3, [nb 2] 6–8, [nb 3] 10, 15, [nb 3] 19–20, 25, [nb 3] 76, 85, [nb 4] 91, 102, 187, 189–197, 218, 223, 225, 233, 250, [nb 3] 255, [nb 3] 260–263, [nb 2] [nb 3] [nb 5] 268, 271–273, 292, [nb 3] 302, [nb 6] 328, [nb 3] 332, [nb 3] 333–337, [nb 3] 362, [nb 3] 365, [nb 3] 415, [nb 6] 423, 438–440, [nb 2] 443, [nb 2] 445, 447, 449, 451, 484, [nb 3] 498, 505–506, 509–510, [nb 3] 543, 556, 558, 562, [nb 6] 571, 595, 599, 600, 722–723, 739, 742, 744, 746, [nb 3] 752, [nb 3] 756, 760–765, 774, [nb 3] 777–785, [nb 3] 790, 797, [nb 3] 801, 822–823, [nb 3] 832, 835, 844, [nb 3] 886–889, [nb 7] [nb 5] 897, 914, [nb 4] 915, 920, 930–931, 936, 940–941, 944–950, [nb 3] [nb 4] 953, 960, 963, 989–990, 1010 and 1026. [nb 7] The Dover Publications paperback edition ( SBN   486612724) cover names the second editor as "Irene A. Segun" instead of Stegun. The ninth reprint edition by Dover incorporates additional corrections on pages 18, 79, 80, 82, 408, 450, 786, 825 and 934. Unresolved errata include: [nb 8] [nb 6] [nb 9] [nb 10]

Related Research Articles

In mathematics, the family of Debye functions is defined by

In mathematics, the Legendre forms of elliptic integrals are a canonical set of three elliptic integrals to which all others may be reduced. Legendre chose the name elliptic integrals because the second kind gives the arc length of an ellipse of unit semi-major axis and eccentricity .

The Mathematical Tables Project was one of the largest and most sophisticated computing organizations that operated prior to the invention of the digital electronic computer. Begun in the United States in 1938 as a project of the Works Progress Administration (WPA), it employed 450 unemployed clerks to tabulate higher mathematical functions, such as exponential functions, logarithms, and trigonometric functions. These tables were eventually published in a 28-volume set by Columbia University Press.

<span class="mw-page-title-main">Milton Abramowitz</span> Jewish American mathematician (1915–1958)

Milton Abramowitz was a Jewish American mathematician at the National Bureau of Standards who, with Irene Stegun, edited a classic book of mathematical tables called Handbook of Mathematical Functions, widely known as Abramowitz and Stegun. Abramowitz died of a heart attack in 1958, at which time the book was not yet completed but was well underway. Stegun took over management of the project and was able to finish the work by 1964, working under the direction of the NBS Chief of Numerical Analysis Philip J. Davis, who was also a contributor to the book.

Handbook of Mathematical Functions may refer to:

In mathematics, and in particular the study of Weierstrass elliptic functions, the equianharmonic case occurs when the Weierstrass invariants satisfy g2 = 0 and g3 = 1. This page follows the terminology of Abramowitz and Stegun; see also the lemniscatic case.

In mathematics, Gegenbauer polynomials or ultraspherical polynomialsC(α)
n(x) are orthogonal polynomials on the interval [−1,1] with respect to the weight function (1 − x2)α–1/2. They generalize Legendre polynomials and Chebyshev polynomials, and are special cases of Jacobi polynomials. They are named after Leopold Gegenbauer.

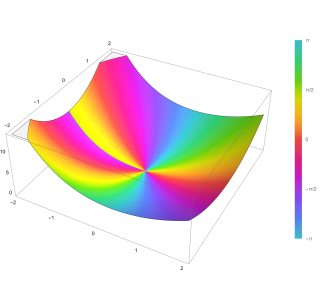
<span class="mw-page-title-main">Whittaker function</span> In mathematics, a solution to a modified form of the confluent hypergeometric equation

In mathematics, a Whittaker function is a special solution of Whittaker's equation, a modified form of the confluent hypergeometric equation introduced by Whittaker (1903) to make the formulas involving the solutions more symmetric. More generally, Jacquet (1966, 1967) introduced Whittaker functions of reductive groups over local fields, where the functions studied by Whittaker are essentially the case where the local field is the real numbers and the group is SL2(R).

In mathematics, series acceleration is one of a collection of sequence transformations for improving the rate of convergence of a series. Techniques for series acceleration are often applied in numerical analysis, where they are used to improve the speed of numerical integration. Series acceleration techniques may also be used, for example, to obtain a variety of identities on special functions. Thus, the Euler transform applied to the hypergeometric series gives some of the classic, well-known hypergeometric series identities.

<span class="mw-page-title-main">Irene Stegun</span> American mathematician

Irene Ann Stegun was an American mathematician at the National Bureau of Standards who edited a classic book of mathematical tables called A Handbook of Mathematical Functions, widely known as Abramowitz and Stegun.

There are a number of notational systems for the Jacobi theta functions. The notations given in the Wikipedia article define the original function

The Digital Library of Mathematical Functions (DLMF) is an online project at the National Institute of Standards and Technology (NIST) to develop a database of mathematical reference data for special functions and their applications. It is intended as an update of Abramowitz's and Stegun's Handbook of Mathematical Functions (A&S). It was published online on 7 May 2010, though some chapters appeared earlier. In the same year it appeared at Cambridge University Press under the title NIST Handbook of Mathematical Functions.

Lucy Joan Slater was a mathematician who worked on hypergeometric functions, and who found many generalizations of the Rogers–Ramanujan identities.

The Sievert integral, named after Swedish medical physicist Rolf Sievert, is a special function commonly encountered in radiation transport calculations.

In mathematics, Boole's rule, named after George Boole, is a method of numerical integration.

In mathematics, the Jacobi zeta functionZ(u) is the logarithmic derivative of the Jacobi theta function Θ(u). It is also commonly denoted as

In statistics, the Cunningham function or Pearson–Cunningham function ωm,n(x) is a generalisation of a special function introduced by Pearson (1906) and studied in the form here by Cunningham (1908). It can be defined in terms of the confluent hypergeometric function U, by

In mathematics, Einstein function is a name occasionally used for one of the functions

In mathematics, the Neville theta functions, named after Eric Harold Neville, are defined as follows:

<i>Gradshteyn and Ryzhik</i> Table of integrals compiled by I. S. Gradshteyn and I. M. Ryzhik

Gradshteyn and Ryzhik (GR) is the informal name of a comprehensive table of integrals originally compiled by the Russian mathematicians I. S. Gradshteyn and I. M. Ryzhik. Its full title today is Table of Integrals, Series, and Products.

References

  1. 1 2 Olver, Frank William John; Lozier, Daniel W.; Boisvert, Ronald F.; Clark, Charles W., eds. (2010). NIST Handbook of Mathematical Functions. National Institute of Standards and Technology (NIST), U.S. Department of Commerce, Cambridge University Press. ISBN   978-0-521-19225-5. MR   2723248.
  2. 1 2 Miller, David Wendell (February 1968). "Abramowitz, M., And I. A. Stegun, Handbook of Mathematical Functions. New York: Dover Publications, Inc., 1965, 1046 pp., $4.50 (paperback)". Application Series. Management Science (review). Vol. 14, no. 6 (#2). p. B-404. JSTOR   2628175 . Retrieved 2021-12-31.
  3. ↑ Wrench, Jr., John William (April 1965). "Reviews and Descriptions of Tables and Books 1: Milton Abramowitz & Irene A. Stegun, Editors, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, Applied Mathematics Series, No. 55, U. S. Government Printing Office, Washington, D. C., 1964, xiv + 1046p., 27 cm. Price $6.50" (PDF). Mathematics of Computation . 19 (89): 147–149. doi:10.2307/2004114. eISSN   1088-6842. ISSN   0025-5718. JSTOR   2004114. MSC:A-F,H-M,R,SX. Archived (PDF) from the original on 2021-09-09. Retrieved 2016-03-13.
  4. ↑ Boisvert, Ronald F.; Clark, Charles W.; Lozier, Daniel W.; Olver, Frank William John (2011). "A Special Functions Handbook for the Digital Age" (PDF). Notices of the American Mathematical Society (NAMS). 58 (7): 905–911. Archived (PDF) from the original on 2021-09-09. Retrieved 2016-03-13.
  5. ↑ Berry, Michael (1997-11-22). "Christmas books: ... Or maybe two or three ..." New Scientist . Retrieved 2016-03-13.
  6. ↑ "NIST at 100: Foundations for Progress, 1964: Mathematics Handbook Becomes Best Seller". 2001. Archived from the original on 2016-03-13. Retrieved 2016-03-13.
  7. ↑ Cloud, John D.; Denman, Harry H.; Wrench, Jr., John William (April 1965). "Table Errata 362: Milton Abramowitz & Irene A. Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, National Bureau of Standards, No. 55, U. S. Government Printing Office, Washington, D. C., 1964" (PDF). Mathematics of Computation . 19 (89): 174–175. eISSN   1088-6842. ISSN   0025-5718. JSTOR   2004148. MTE:362. Archived (PDF) from the original on 2021-09-09. Retrieved 2016-03-13.
  8. ↑ Stegun, Irene Ann; Aggarwal, H. R.; Ablow, Clarence M. (April 1965). "Table Errata 365: Milton Abramowitz & Irene A. Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, National Bureau of Standards Applied Mathematics Series, No. 55, U. S. Government Printing Office, Washington, D. C., 1964" (PDF). Mathematics of Computation . 19 (90): 360–363. eISSN   1088-6842. ISSN   0025-5718. JSTOR   2003399. MTE:365. Archived (PDF) from the original on 2021-09-09. Retrieved 2016-03-13.
  9. ↑ Thacher, Jr., Henry C. (July 1965). "Errata 373: Milton Abramowitz & Irene A. Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, National Bureau of Standards, Applied Mathematics Series, No. 55, U. S. Government Printing Office, Washington, D. C., first printing, June 1964" (PDF). Mathematics of Computation . 19 (91): 527–528. doi: 10.2307/2003725 . eISSN   1088-6842. ISSN   0025-5718. JSTOR   2003725. MTE:373. Archived (PDF) from the original on 2021-09-09. Retrieved 2016-03-13.
  10. ↑ Manning, Irwin; Templeton, James Gilbert Cooper; Thacher, Jr., Henry C. (October 1965). "Errata 376: Milton Abramowitz & Irene A. Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, National Bureau of Standards, Applied Mathematics Series, No. 55, U. S. Government Printing Office, Washington, D. C., 1964" (PDF). Mathematics of Computation . 19 (92): 705–706. doi: 10.2307/2003991 . eISSN   1088-6842. ISSN   0025-5718. JSTOR   2003991. MTE:376. Archived (PDF) from the original on 2021-09-09. Retrieved 2016-03-13.
  11. 1 2 3 4 Shanks, Daniel; Greenebaum, Michael (January 1966). "Errata 379: Milton Abramowitz & Irene A. Stegun, Editors, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, National Bureau of Standards, Applied Mathematics Series, No. 55, U. S. Government Printing Office, Washington, D. C., 1964, and all known reprints" (PDF). Mathematics of Computation . 20 (93): 202–206. eISSN   1088-6842. ISSN   0025-5718. JSTOR   2004328. MTE:379. Archived (PDF) from the original on 2021-09-09. Retrieved 2016-03-13.
  12. ↑ Wood, Van E.; Gamper, René (April 1966). "Errata 388: Milton Abramowitz & Irene A. Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, National Bureau of Standards, Applied Mathematics Series, No. 55, U.S. Government Printing Office, Washington, D.C., first printing, June 1964" (PDF). Mathematics of Computation . 20 (94): 344. eISSN   1088-6842. ISSN   0025-5718. JSTOR   2003533. MTE:388. Archived (PDF) from the original on 2021-09-09. Retrieved 2016-03-13.
  13. 1 2 3 Salzer, Herbert E.; Johnson, Robert S.; Fettis, Henry E.; Caslin, James C.; Concus, Paul (July 1966). "Errata 393: Milton Abramowitz & Irene A. Stegun, Editors, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, National Bureau of Standards, Applied Mathematics Series, No. 55, U. S. Government Printing Office, Washington, D.C., 1964" (PDF). Mathematics of Computation . 20 (95): 469–471. doi: 10.2307/2003630 . eISSN   1088-6842. ISSN   0025-5718. JSTOR   2003630. MTE:393. Archived (PDF) from the original on 2021-09-09. Retrieved 2016-03-13.
  14. 1 2 Danos, Michael; Rafelski, Johann; Abramowitz, Milton; Stegun, Irene Ann, eds. (1984). Pocketbook of Mathematical Functions. Thun, Frankfurt/Main: Verlag Harri Deutsch. ISBN   978-3-87144-818-8 . Retrieved 2016-03-13. (468 pages)
  15. 1 2 3 4 5 Wrench, Jr., John William (April 1988). "Reviews and Descriptions of Tables and Books 18: Milton Abramowitz and Irene A. Stegun. Pocketbook of Mathematical Functions - Abridged Edition of Handbook of Mathematical Functions. Material selected by Michael Danos and Johann Rafelski" (PDF). Mathematics of Computation . 50 (182): 646–647. doi:10.2307/2008636. eISSN   1088-6842. ISSN   0025-5718. JSTOR   2008636. MSC:33-00,65A05. Archived (PDF) from the original on 2021-09-09. Retrieved 2016-03-13.
  16. ↑ Zucker, Ruth (1983) [June 1964]. "Chapter 25.4.14: Numerical Interpolation, Differentiation, and Integration - Integration - Numerical Analysis". In Abramowitz, Milton; Stegun, Irene Ann (eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 886. ISBN   978-0-486-61272-0. LCCN   64-60036. MR   0167642. LCCN   65-12253.
  17. ↑ "Boole's Rule - from Wolfram MathWorld". Mathworld.wolfram.com. 2009-10-27. Archived from the original on 2021-12-01. Retrieved 2009-11-13.
  18. Fettis, Henry E. (October 1969). "Table Errata 444: Milton Abramowitz & Irene A. Stegun, Editors, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, National Bureau of Standards, Applied Mathematics Series, No. 55, U. S. Government Printing Office, Washington, D. C., 1964, and all known reprints" (PDF). Mathematics of Computation . 23 (108): 891. eISSN   1088-6842. ISSN   0025-5718. JSTOR   2004993. MTE:444. Archived (PDF) from the original on 2019-05-03. Retrieved 2016-03-13.
  19. Davenport, James Harold (October 2002). "Table Errata 638: Abramowitz, M., & Stegun, I. Handbook of mathematical functions with formulas, graphs, and mathematical tables". Mathematics of Computation . 71 (240): 1801. eISSN   1088-6842. ISSN   0025-5718. JSTOR   4099976. MTE:638. PII:S0025-5718-97-00823-5. CODEN   MCMPAF.

Further reading

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.