Acoustic attenuation

Last updated

In acoustics, acoustic attenuation is a measure of the energy loss of sound propagation through an acoustic transmission medium. Most media have viscosity and are therefore not ideal media. When sound propagates in such media, there is always thermal consumption of energy caused by viscosity. This effect can be quantified through the Stokes's law of sound attenuation. Sound attenuation may also be a result of heat conductivity in the media as has been shown by G. Kirchhoff in 1868. [1] [2] The Stokes-Kirchhoff attenuation formula takes into account both viscosity and thermal conductivity effects.

Contents

For heterogeneous media, besides media viscosity, acoustic scattering is another main reason for removal of acoustic energy. Acoustic attenuation in a lossy medium plays an important role in many scientific researches and engineering fields, such as medical ultrasonography, vibration and noise reduction. [3] [4] [5] [6]

Power-law frequency-dependent acoustic attenuation

Many experimental and field measurements show that the acoustic attenuation coefficient of a wide range of viscoelastic materials, such as soft tissue, polymers, soil, and porous rock, can be expressed as the following power law with respect to frequency: [7] [8] [9]

where is the angular frequency, P the pressure, the wave propagation distance, the attenuation coefficient, and and the frequency-dependent exponent are real non-negative material parameters obtained by fitting experimental data; the value of ranges from 0 to 4. Acoustic attenuation in water is frequency-squared dependent, namely . Acoustic attenuation in many metals and crystalline materials is frequency-independent, namely . [10] In contrast, it is widely noted that the of viscoelastic materials is between 0 and 2. [7] [8] [11] [12] [13] For example, the exponent of sediment, soil, and rock is about 1, and the exponent of most soft tissues is between 1 and 2. [7] [8] [11] [12] [13]

The classical dissipative acoustic wave propagation equations are confined to the frequency-independent and frequency-squared dependent attenuation, such as the damped wave equation and the approximate thermoviscous wave equation. In recent decades, increasing attention and efforts have been focused on developing accurate models to describe general power law frequency-dependent acoustic attenuation. [8] [11] [14] [15] [16] [17] [18] Most of these recent frequency-dependent models are established via the analysis of the complex wave number and are then extended to transient wave propagation. [19] The multiple relaxation model considers the power law viscosity underlying different molecular relaxation processes. [17] Szabo [8] proposed a time convolution integral dissipative acoustic wave equation. On the other hand, acoustic wave equations based on fractional derivative viscoelastic models are applied to describe the power law frequency dependent acoustic attenuation. [18] Chen and Holm proposed the positive fractional derivative modified Szabo's wave equation [11] and the fractional Laplacian wave equation. [11] See [20] for a paper which compares fractional wave equations with model power-law attenuation. This book on power-law attenuation also covers the topic in more detail. [21]

The phenomenon of attenuation obeying a frequency power-law may be described using a causal wave equation, derived from a fractional constitutive equation between stress and strain. This wave equation incorporates fractional time derivatives:

See also [14] and the references therein.

Such fractional derivative models are linked to the commonly recognized hypothesis that multiple relaxation phenomena (see Nachman et al. [17] ) give rise to the attenuation measured in complex media. This link is further described in [22] and in the survey paper. [23]

For frequency band-limited waves, Ref. [24] describes a model-based method to attain causal power-law attenuation using a set of discrete relaxation mechanisms within the Nachman et al. framework. [17]

In porous fluid-saturated sedimentary rocks, such as sandstone, acoustic attenuation is primarily caused by the wave-induced flow of the pore fluid relative to the solid frame, with varying between 0.5 and 1.5. [25]

See also

Related Research Articles

In physics, attenuation is the gradual loss of flux intensity through a medium. For instance, dark glasses attenuate sunlight, lead attenuates X-rays, and water and air attenuate both light and sound at variable attenuation rates.

The propagation constant of a sinusoidal electromagnetic wave is a measure of the change undergone by the amplitude and phase of the wave as it propagates in a given direction. The quantity being measured can be the voltage, the current in a circuit, or a field vector such as electric field strength or flux density. The propagation constant itself measures the dimensionless change in magnitude or phase per unit length. In the context of two-port networks and their cascades, propagation constant measures the change undergone by the source quantity as it propagates from one port to the next.

Fractional calculus is a branch of mathematical analysis that studies the several different possibilities of defining real number powers or complex number powers of the differentiation operator

In electromagnetics, an evanescent field, or evanescent wave, is an oscillating electric and/or magnetic field that does not propagate as an electromagnetic wave but whose energy is spatially concentrated in the vicinity of the source. Even when there is a propagating electromagnetic wave produced, one can still identify as an evanescent field the component of the electric or magnetic field that cannot be attributed to the propagating wave observed at a distance of many wavelengths.

<span class="mw-page-title-main">Rayleigh–Taylor instability</span> Unstable behavior of two contacting fluids of different densities

The Rayleigh–Taylor instability, or RT instability, is an instability of an interface between two fluids of different densities which occurs when the lighter fluid is pushing the heavier fluid. Examples include the behavior of water suspended above oil in the gravity of Earth, mushroom clouds like those from volcanic eruptions and atmospheric nuclear explosions, supernova explosions in which expanding core gas is accelerated into denser shell gas, instabilities in plasma fusion reactors and inertial confinement fusion.

<span class="mw-page-title-main">Dielectric spectroscopy</span>

Dielectric spectroscopy measures the dielectric properties of a medium as a function of frequency. It is based on the interaction of an external field with the electric dipole moment of the sample, often expressed by permittivity.

<span class="mw-page-title-main">Post-Newtonian expansion</span> Method of approximation in general relativity

In general relativity, post-Newtonian expansions are used for finding an approximate solution of Einstein field equations for the metric tensor. The approximations are expanded in small parameters that express orders of deviations from Newton's law of universal gravitation. This allows approximations to Einstein's equations to be made in the case of weak fields. Higher-order terms can be added to increase accuracy, but for strong fields sometimes it is preferable to solve the complete equations numerically. This method is a common mark of effective field theories. In the limit, when the small parameters are equal to 0, the post-Newtonian expansion reduces to Newton's law of gravity.

The Cole–Cole equation is a relaxation model that is often used to describe dielectric relaxation in polymers.

Acoustic waves are a type of energy propagation through a medium by means of adiabatic loading and unloading. Important quantities for describing acoustic waves are acoustic pressure, particle velocity, particle displacement and acoustic intensity. Acoustic waves travel with a characteristic acoustic velocity that depends on the medium they're passing through. Some examples of acoustic waves are audible sound from a speaker, seismic waves, or ultrasound used for medical imaging.

In acoustics, Stokes's law of sound attenuation is a formula for the attenuation of sound in a Newtonian fluid, such as water or air, due to the fluid's viscosity. It states that the amplitude of a plane wave decreases exponentially with distance traveled, at a rate α given by

An acoustic rheometer is a device used to measure the rheological properties of fluids, such as viscosity and elasticity, by utilizing sound waves. It works by generating acoustic waves in the fluid and analyzing the changes in the wave propagation caused by the fluid's rheological behavior. An acoustic rheometer uses a piezo-electric crystal to generate the acoustic waves, applying an oscillating extensional stress to the system. System response can be interpreted in terms of extensional rheology.

Acoustic streaming is a steady flow in a fluid driven by the absorption of high amplitude acoustic oscillations. This phenomenon can be observed near sound emitters, or in the standing waves within a Kundt's tube. Acoustic streaming was explained first by Lord Rayleigh in 1884. It is the less-known opposite of sound generation by a flow.

<span class="mw-page-title-main">Viscosity</span> Resistance of a fluid to shear deformation

The viscosity of a fluid is a measure of its resistance to deformation at a given rate. For liquids, it corresponds to the informal concept of "thickness": for example, syrup has a higher viscosity than water. Viscosity is defined scientifically as a force multiplied by a time divided by an area. Thus its SI units are newton-seconds per square metre, or pascal-seconds.

<span class="mw-page-title-main">Cnoidal wave</span> Nonlinear and exact periodic wave solution of the Korteweg–de Vries equation

In fluid dynamics, a cnoidal wave is a nonlinear and exact periodic wave solution of the Korteweg–de Vries equation. These solutions are in terms of the Jacobi elliptic function cn, which is why they are coined cnoidal waves. They are used to describe surface gravity waves of fairly long wavelength, as compared to the water depth.

<span class="mw-page-title-main">Substrate-integrated waveguide</span> Waveguide formed by posts inserted in a dielectric substrate

A substrate-integrated waveguide (SIW) is a synthetic rectangular electromagnetic waveguide formed in a dielectric substrate by densely arraying metallized posts or via holes that connect the upper and lower metal plates of the substrate. The waveguide can be easily fabricated with low-cost mass-production using through-hole techniques, where the post walls consists of via fences. SIW is known to have similar guided wave and mode characteristics to conventional rectangular waveguide with equivalent guide wavelength.

In mathematical physics, the Whitham equation is a non-local model for non-linear dispersive waves.

In the fields of dynamical systems and control theory, a fractional-order system is a dynamical system that can be modeled by a fractional differential equation containing derivatives of non-integer order. Such systems are said to have fractional dynamics. Derivatives and integrals of fractional orders are used to describe objects that can be characterized by power-law nonlocality, power-law long-range dependence or fractal properties. Fractional-order systems are useful in studying the anomalous behavior of dynamical systems in physics, electrochemistry, biology, viscoelasticity and chaotic systems.

<span class="mw-page-title-main">Cinna Lomnitz</span> Mexican researcher

Cinna Lomnitz Aronsfrau was a Chilean-Mexican geophysicist known for his contributions in the fields of rock mechanics and seismology.

<span class="mw-page-title-main">Green's law</span> Equation describing evolution of waves in shallow water

In fluid dynamics, Green's law, named for 19th-century British mathematician George Green, is a conservation law describing the evolution of non-breaking, surface gravity waves propagating in shallow water of gradually varying depth and width. In its simplest form, for wavefronts and depth contours parallel to each other, it states:

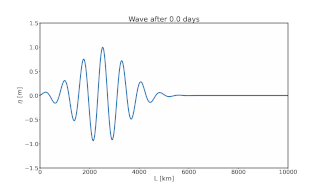
<span class="mw-page-title-main">Topographic Rossby waves</span> Description of waves in the ocean and atmosphere created by bottom irregularities

Topographic Rossby waves are geophysical waves that form due to bottom irregularities. For ocean dynamics, the bottom irregularities are on the ocean floor such as the mid-ocean ridge. For atmospheric dynamics, the other primary branch of geophysical fluid dynamics, the bottom irregularities are found on land, for example in the form of mountains. Topographic Rossby waves are one of two types of geophysical waves named after the meteorologist Carl-Gustaf Rossby. The other type of Rossby waves are called planetary Rossby waves and have a different physical origin. Planetary Rossby waves form due to the changing Coriolis parameter over the earth. Rossby waves are quasi-geostrophic, dispersive waves. This means that not only the Coriolis force and the pressure-gradient force influence the flow, as in geostrophic flow, but also inertia.

References

  1. ↑ Kirchhoff, G. (1868). "Ueber den Einfluss der Wärmeleitung in einem Gase auf die Schallbewegung". Annalen der Physik und Chemie. 210 (6): 177–193. Bibcode:1868AnP...210..177K. doi:10.1002/andp.18682100602.
  2. ↑ Benjelloun, Saad; Ghidaglia, Jean-Michel (2020). "On the dispersion relation for compressible Navier-Stokes Equations". arXiv: 2011.06394 [math.AP].
  3. ↑ Chen, Yangkang; Ma, Jitao (May–June 2014). "Random noise attenuation by f-x empirical-mode decomposition predictive filtering". Geophysics. 79 (3): V81–V91. Bibcode:2014Geop...79...81C. doi:10.1190/GEO2013-0080.1.
  4. ↑ Chen, Yangkang; Zhou, Chao; Yuan, Jiang; Jin, Zhaoyu (2014). "Application of empirical mode decomposition in random noise attenuation of seismic data". Journal of Seismic Exploration. 23: 481–495.
  5. ↑ Chen, Yangkang; Zhang, Guoyin; Gan, Shuwei; Zhang, Chenglin (2015). "Enhancing seismic reflections using empirical mode decomposition in the flattened domain". Journal of Applied Geophysics. 119: 99–105. Bibcode:2015JAG...119...99C. doi:10.1016/j.jappgeo.2015.05.012.
  6. ↑ Chen, Yangkang (2016). "Dip-separated structural filtering using seislet transform and adaptive empirical mode decomposition based dip filter". Geophysical Journal International. 206 (1): 457–469. Bibcode:2016GeoJI.206..457C. doi: 10.1093/gji/ggw165 .
  7. 1 2 3 Szabo, Thomas L.; Wu, Junru (2000). "A model for longitudinal and shear wave propagation in viscoelastic media". The Journal of the Acoustical Society of America. 107 (5): 2437–2446. Bibcode:2000ASAJ..107.2437S. doi:10.1121/1.428630. PMID   10830366.
  8. 1 2 3 4 5 Szabo, Thomas L. (1994). "Time domain wave equations for lossy media obeying a frequency power law". The Journal of the Acoustical Society of America. 96 (1): 491–500. Bibcode:1994ASAJ...96..491S. doi:10.1121/1.410434.
  9. ↑ Chen, W.; Holm, S. (2003). "Modified Szabo's wave equation models for lossy media obeying frequency power law". The Journal of the Acoustical Society of America. 114 (5): 2570–4. arXiv: math-ph/0212076 . Bibcode:2003ASAJ..114.2570C. doi:10.1121/1.1621392. PMID   14649993. S2CID   33635976.
  10. ↑ {{Knopoff, L. Rev. Geophys.|title = Q|year 1964| 2, 625–660| >
  11. 1 2 3 4 5 Chen, W.; Holm, S. (2004). "Fractional Laplacian time-space models for linear and nonlinear lossy media exhibiting arbitrary frequency power-law dependency". The Journal of the Acoustical Society of America. 115 (4): 1424–1430. Bibcode:2004ASAJ..115.1424C. doi:10.1121/1.1646399. PMID   15101619.
  12. 1 2 Carcione, J. M.; Cavallini, F.; Mainardi, F.; Hanyga, A. (2002). "Time-domain Modeling of Constant- Q Seismic Waves Using Fractional Derivatives". Pure and Applied Geophysics. 159 (7–8): 1719–1736. Bibcode:2002PApGe.159.1719C. doi:10.1007/s00024-002-8705-z. S2CID   73598914.
  13. 1 2 d'Astous, F.T.; Foster, F.S. (1986). "Frequency dependence of ultrasound attenuation and backscatter in breast tissue". Ultrasound in Medicine & Biology. 12 (10): 795–808. doi:10.1016/0301-5629(86)90077-3. PMID   3541334.
  14. 1 2 Holm, Sverre; Näsholm, Sven Peter (2011). "A causal and fractional all-frequency wave equation for lossy media". The Journal of the Acoustical Society of America. 130 (4): 2195–2202. Bibcode:2011ASAJ..130.2195H. doi:10.1121/1.3631626. hdl: 10852/103311 . PMID   21973374.
  15. ↑ Pritz, T. (2004). "Frequency power law of material damping". Applied Acoustics. 65 (11): 1027–1036. doi:10.1016/j.apacoust.2004.06.001.
  16. ↑ Waters, K.R.; Mobley, J.; Miller, J.G. (2005). "Causality-imposed (Kramers-Kronig) relationships between attenuation and dispersion". IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control. 52 (5): 822–823. doi:10.1109/TUFFC.2005.1503968. PMID   16048183. S2CID   23508424.
  17. 1 2 3 4 Nachman, Adrian I.; Smith, James F.; Waag, Robert C. (1990). "An equation for acoustic propagation in inhomogeneous media with relaxation losses". The Journal of the Acoustical Society of America. 88 (3): 1584–1595. Bibcode:1990ASAJ...88.1584N. doi:10.1121/1.400317.
  18. 1 2 Caputo, M.; Mainardi, F. (1971). "A new dissipation model based on memory mechanism". Pure and Applied Geophysics. 91 (1): 134–147. Bibcode:1971PApGe..91..134C. doi:10.1007/BF00879562. S2CID   121781575.
  19. ↑ Szabo, Thomas L. (13 November 2018). Diagnostic Ultrasound Imaging: Inside Out (Second ed.). Oxford: Academic Press. ISBN   9780123964878.
  20. ↑ Holm, Sverre; Näsholm, Sven Peter (2014). "Comparison of Fractional Wave Equations for Power Law Attenuation in Ultrasound and Elastography". Ultrasound in Medicine & Biology. 40 (4): 695–703. arXiv: 1306.6507 . doi:10.1016/j.ultrasmedbio.2013.09.033. PMID   24433745. S2CID   11983716.
  21. ↑ Holm, S. (2019). Waves with Power-Law Attenuation. Springer/Acoustical Society of America Press. ISBN   9783030149260.
  22. ↑ Näsholm, Sven Peter; Holm, Sverre (2011). "Linking multiple relaxation, power-law attenuation, and fractional wave equations". The Journal of the Acoustical Society of America. 130 (5): 3038–3045. Bibcode:2011ASAJ..130.3038N. doi:10.1121/1.3641457. hdl: 10852/103312 . PMID   22087931.
  23. ↑ Sven Peter Nasholm; Holm, Sverre (2012). "On a Fractional Zener Elastic Wave Equation". Fractional Calculus and Applied Analysis. 16: 26–50. arXiv: 1212.4024 . doi:10.2478/s13540-013-0003-1. S2CID   120348311.
  24. ↑ Näsholm, Sven Peter (2013). "Model-based discrete relaxation process representation of band-limited power-law attenuation". The Journal of the Acoustical Society of America. 133 (3): 1742–1750. arXiv: 1301.5256 . Bibcode:2013ASAJ..133.1742N. doi:10.1121/1.4789001. PMID   23464043. S2CID   22963787.
  25. ↑ Müller, Tobias M.; Gurevich, Boris; Lebedev, Maxim (September 2010). "Seismic wave attenuation and dispersion resulting from wave-induced flow in porous rocks — A review". Geophysics. 75 (5): 75A147–75A164. Bibcode:2010Geop...75A.147M. doi:10.1190/1.3463417. hdl: 20.500.11937/35921 .
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.