In computer science, an array is a data structure consisting of a collection of elements, of same memory size, each identified by at least one array index or key. An array is stored such that the position of each element can be computed from its index tuple by a mathematical formula. The simplest type of data structure is a linear array, also called one-dimensional array.
In computer science, a linked list is a linear collection of data elements whose order is not given by their physical placement in memory. Instead, each element points to the next. It is a data structure consisting of a collection of nodes which together represent a sequence. In its most basic form, each node contains data, and a reference to the next node in the sequence. This structure allows for efficient insertion or removal of elements from any position in the sequence during iteration. More complex variants add additional links, allowing more efficient insertion or removal of nodes at arbitrary positions. A drawback of linked lists is that data access time is linear in respect to the number of nodes in the list. Because nodes are serially linked, accessing any node requires that the prior node be accessed beforehand. Faster access, such as random access, is not feasible. Arrays have better cache locality compared to linked lists.

In computer science, a sorting algorithm is an algorithm that puts elements of a list into an order. The most frequently used orders are numerical order and lexicographical order, and either ascending or descending. Efficient sorting is important for optimizing the efficiency of other algorithms that require input data to be in sorted lists. Sorting is also often useful for canonicalizing data and for producing human-readable output.
In computing, an optimizing compiler is a compiler that tries to minimize or maximize some attributes of an executable computer program. Common requirements are to minimize a program's execution time, memory footprint, storage size, and power consumption.
In computer science, locality of reference, also known as the principle of locality, is the tendency of a processor to access the same set of memory locations repetitively over a short period of time. There are two basic types of reference locality – temporal and spatial locality. Temporal locality refers to the reuse of specific data and/or resources within a relatively small time duration. Spatial locality refers to the use of data elements within relatively close storage locations. Sequential locality, a special case of spatial locality, occurs when data elements are arranged and accessed linearly, such as traversing the elements in a one-dimensional array.

In computer science and computer programming, a data type is a collection or grouping of data values, usually specified by a set of possible values, a set of allowed operations on these values, and/or a representation of these values as machine types. A data type specification in a program constrains the possible values that an expression, such as a variable or a function call, might take. On literal data, it tells the compiler or interpreter how the programmer intends to use the data. Most programming languages support basic data types of integer numbers, floating-point numbers, characters and Booleans.
In computer programming, a type system is a logical system comprising a set of rules that assigns a property called a type to every term. Usually the terms are various language constructs of a computer program, such as variables, expressions, functions, or modules. A type system dictates the operations that can be performed on a term. For variables, the type system determines the allowed values of that term. Type systems formalize and enforce the otherwise implicit categories the programmer uses for algebraic data types, data structures, or other components.

In numerical analysis and scientific computing, a sparse matrix or sparse array is a matrix in which most of the elements are zero. There is no strict definition regarding the proportion of zero-value elements for a matrix to qualify as sparse but a common criterion is that the number of non-zero elements is roughly equal to the number of rows or columns. By contrast, if most of the elements are non-zero, the matrix is considered dense. The number of zero-valued elements divided by the total number of elements is sometimes referred to as the sparsity of the matrix.
In computer programming, a dope vector is a data structure used to hold information about a data object, especially its memory layout.
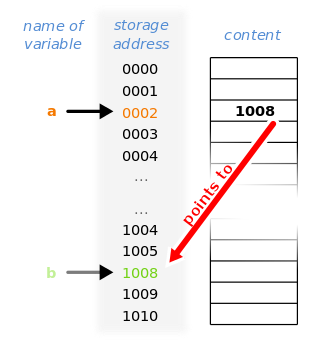
In computer science, a pointer is an object in many programming languages that stores a memory address. This can be that of another value located in computer memory, or in some cases, that of memory-mapped computer hardware. A pointer references a location in memory, and obtaining the value stored at that location is known as dereferencing the pointer. As an analogy, a page number in a book's index could be considered a pointer to the corresponding page; dereferencing such a pointer would be done by flipping to the page with the given page number and reading the text found on that page. The actual format and content of a pointer variable is dependent on the underlying computer architecture.

Curve fitting is the process of constructing a curve, or mathematical function, that has the best fit to a series of data points, possibly subject to constraints. Curve fitting can involve either interpolation, where an exact fit to the data is required, or smoothing, in which a "smooth" function is constructed that approximately fits the data. A related topic is regression analysis, which focuses more on questions of statistical inference such as how much uncertainty is present in a curve that is fitted to data observed with random errors. Fitted curves can be used as an aid for data visualization, to infer values of a function where no data are available, and to summarize the relationships among two or more variables. Extrapolation refers to the use of a fitted curve beyond the range of the observed data, and is subject to a degree of uncertainty since it may reflect the method used to construct the curve as much as it reflects the observed data.
In computer science, array programming refers to solutions that allow the application of operations to an entire set of values at once. Such solutions are commonly used in scientific and engineering settings.
In computing, a group of parallel arrays is a form of implicit data structure that uses multiple arrays to represent a singular array of records. It keeps a separate, homogeneous data array for each field of the record, each having the same number of elements. Then, objects located at the same index in each array are implicitly the fields of a single record. Pointers from one object to another are replaced by array indices. This contrasts with the normal approach of storing all fields of each record together in memory. For example, one might declare an array of 100 names, each a string, and 100 ages, each an integer, associating each name with the age that has the same index.

In computing, row-major order and column-major order are methods for storing multidimensional arrays in linear storage such as random access memory.

Quicksort is an efficient, general-purpose sorting algorithm. Quicksort was developed by British computer scientist Tony Hoare in 1959 and published in 1961. It is still a commonly used algorithm for sorting. Overall, it is slightly faster than merge sort and heapsort for randomized data, particularly on larger distributions.
In program analysis, shape analysis is a static code analysis technique that discovers and verifies properties of linked, dynamically allocated data structures in computer programs. It is typically used at compile time to find software bugs or to verify high-level correctness properties of programs. In Java programs, it can be used to ensure that a sort method correctly sorts a list. For C programs, it might look for places where a block of memory is not properly freed.
In computer science, pointer analysis, or points-to analysis, is a static code analysis technique that establishes which pointers, or heap references, can point to which variables, or storage locations. It is often a component of more complex analyses such as escape analysis. A closely related technique is shape analysis.
Use of the polyhedral model within a compiler requires software to represent the objects of this framework and perform operations upon them.
In computer science, array is a data type that represents a collection of elements, each selected by one or more indices that can be computed at run time during program execution. Such a collection is usually called an array variable or array value. By analogy with the mathematical concepts vector and matrix, array types with one and two indices are often called vector type and matrix type, respectively. More generally, a multidimensional array type can be called a tensor type, by analogy with the physical concept, tensor.
This glossary of computer science is a list of definitions of terms and concepts used in computer science, its sub-disciplines, and related fields, including terms relevant to software, data science, and computer programming.






