
In physics, physical chemistry and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids—liquids and gases. It has several subdisciplines, including aerodynamics and hydrodynamics. Fluid dynamics has a wide range of applications, including calculating forces and moments on aircraft, determining the mass flow rate of petroleum through pipelines, predicting weather patterns, understanding nebulae in interstellar space and modelling fission weapon detonation.

The Mach number, often only Mach, is a dimensionless quantity in fluid dynamics representing the ratio of flow velocity past a boundary to the local speed of sound. It is named after the Austrian physicist and philosopher Ernst Mach.

Magnetohydrodynamics is a model of electrically conducting fluids that treats all interpenetrating particle species together as a single continuous medium. It is primarily concerned with the low-frequency, large-scale, magnetic behavior in plasmas and liquid metals and has applications in numerous fields including geophysics, astrophysics, and engineering.

The Navier–Stokes equations are partial differential equations which describe the motion of viscous fluid substances. They were named after French engineer and physicist Claude-Louis Navier and the Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes).

Bernoulli's principle is a key concept in fluid dynamics that relates pressure, speed and height. Bernoulli's principle states that an increase in the speed of a fluid occurs simultaneously with a decrease in static pressure or the fluid's potential energy. The principle is named after the Swiss mathematician and physicist Daniel Bernoulli, who published it in his book Hydrodynamica in 1738. Although Bernoulli deduced that pressure decreases when the flow speed increases, it was Leonhard Euler in 1752 who derived Bernoulli's equation in its usual form.
The vorticity equation of fluid dynamics describes the evolution of the vorticity ω of a particle of a fluid as it moves with its flow; that is, the local rotation of the fluid. The governing equation is:
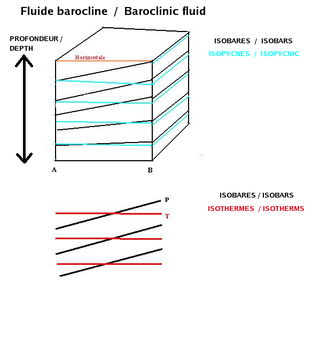
In fluid dynamics, the baroclinity of a stratified fluid is a measure of how misaligned the gradient of pressure is from the gradient of density in a fluid. In meteorology a baroclinic flow is one in which the density depends on both temperature and pressure. A simpler case, barotropic flow, allows for density dependence only on pressure, so that the curl of the pressure-gradient force vanishes.
In fluid dynamics, the Boussinesq approximation is used in the field of buoyancy-driven flow. It ignores density differences except where they appear in terms multiplied by g, the acceleration due to gravity. The essence of the Boussinesq approximation is that the difference in inertia is negligible but gravity is sufficiently strong to make the specific weight appreciably different between the two fluids. Sound waves are impossible/neglected when the Boussinesq approximation is used since sound waves move via density variations.

In fluid dynamics, the Euler equations are a set of quasilinear partial differential equations governing adiabatic and inviscid flow. They are named after Leonhard Euler. In particular, they correspond to the Navier–Stokes equations with zero viscosity and zero thermal conductivity.
In fluid mechanics, or more generally continuum mechanics, incompressible flow refers to a flow in which the material density is constant within a fluid parcel—an infinitesimal volume that moves with the flow velocity. An equivalent statement that implies incompressibility is that the divergence of the flow velocity is zero.

Internal waves are gravity waves that oscillate within a fluid medium, rather than on its surface. To exist, the fluid must be stratified: the density must change with depth/height due to changes, for example, in temperature and/or salinity. If the density changes over a small vertical distance, the waves propagate horizontally like surface waves, but do so at slower speeds as determined by the density difference of the fluid below and above the interface. If the density changes continuously, the waves can propagate vertically as well as horizontally through the fluid.

Smoothed-particle hydrodynamics (SPH) is a computational method used for simulating the mechanics of continuum media, such as solid mechanics and fluid flows. It was developed by Gingold and Monaghan and Lucy in 1977, initially for astrophysical problems. It has been used in many fields of research, including astrophysics, ballistics, volcanology, and oceanography. It is a meshfree Lagrangian method, and the resolution of the method can easily be adjusted with respect to variables such as density.
In physics, magnetosonic waves, also known as magnetoacoustic waves, are low-frequency compressive waves driven by mutual interaction between an electrically conducting fluid and a magnetic field. They are associated with compression and rarefaction of both the fluid and the magnetic field, as well as with an effective tension that acts to straighten bent magnetic field lines. The properties of magnetosonic waves are highly dependent on the angle between the wavevector and the equilibrium magnetic field and on the relative importance of fluid and magnetic processes in the medium. They only propagate with frequencies much smaller than the ion cyclotron or ion plasma frequencies of the medium, and they are nondispersive at small amplitudes.

In fluid mechanics and hydraulics, open-channel flow is a type of liquid flow within a conduit with a free surface, known as a channel. The other type of flow within a conduit is pipe flow. These two types of flow are similar in many ways but differ in one important respect: open-channel flow has a free surface, whereas pipe flow does not, resulting in flow dominated by gravity but not hydraulic pressure.
Aeroacoustics is a branch of acoustics that studies noise generation via either turbulent fluid motion or aerodynamic forces interacting with surfaces. Noise generation can also be associated with periodically varying flows. A notable example of this phenomenon is the Aeolian tones produced by wind blowing over fixed objects.

The Jeans instability is a concept in astrophysics that describes an instability that leads to the gravitational collapse of a cloud of gas or dust. It causes the collapse of interstellar gas clouds and subsequent star formation. It occurs when the internal gas pressure is not strong enough to prevent the gravitational collapse of a region filled with matter. It is named after James Jeans.
In fluid dynamics, dynamic pressure is the quantity defined by:
In magnetohydrodynamics (MHD), shocks and discontinuities are transition layers where properties of a plasma change from one equilibrium state to another. The relation between the plasma properties on both sides of a shock or a discontinuity can be obtained from the conservative form of the MHD equations, assuming conservation of mass, momentum, energy and of .
In fluid dynamics, Airy wave theory gives a linearised description of the propagation of gravity waves on the surface of a homogeneous fluid layer. The theory assumes that the fluid layer has a uniform mean depth, and that the fluid flow is inviscid, incompressible and irrotational. This theory was first published, in correct form, by George Biddell Airy in the 19th century.

In fluid dynamics, the radiation stress is the depth-integrated – and thereafter phase-averaged – excess momentum flux caused by the presence of the surface gravity waves, which is exerted on the mean flow. The radiation stresses behave as a second-order tensor.


























