Common-method variance

Last updated

In applied statistics, (e.g., applied to the social sciences and psychometrics), common-method variance (CMV) is the spurious "variance that is attributable to the measurement method rather than to the constructs the measures are assumed to represent" [1] or equivalently as "systematic error variance shared among variables measured with and introduced as a function of the same method and/or source". [2] For example, an electronic survey method might influence results for those who might be unfamiliar with an electronic survey interface differently than for those who might be familiar. If measures are affected by CMV or common-method bias, the intercorrelations among them can be inflated or deflated depending upon several factors. [3] Although it is sometimes assumed that CMV affects all variables, evidence suggests that whether or not the correlation between two variables is affected by CMV is a function of both the method and the particular constructs being measured. [4]

Contents

Remedies

Ex ante remedies

Several ex ante remedies exist that help to avoid or minimize possible common method variance. Important remedies have been compiled and discussed by Chang et al. (2010), Lindell & Whitney (2001) and Podsakoff et al. (2003). [5] [6] [1]

Ex post remedies

Using simulated data sets, Richardson et al. (2009) investigate three ex post techniques to test for common method variance: the correlational marker technique, the confirmatory factor analysis (CFA) marker technique, and the unmeasured latent method construct (ULMC) technique. Only the CFA marker technique turns out to provide some value, whereas the commonly used Harman test does not turn out to provide such value. [2] A comprehensive example of this technique has been demonstrated by Williams et al. (2010). [7] Kock (2015) discusses a full collinearity test that is successful in the identification of common method bias with a model that nevertheless passes standard convergent and discriminant validity assessment criteria based on a CFA. [8] [9]

Related Research Articles

Psychological statistics is application of formulas, theorems, numbers and laws to psychology. Statistical Methods for psychology include development and application statistical theory and methods for modeling psychological data. These methods include psychometrics, Factor analysis, Experimental Designs, and Multivariate Behavioral Research. The article also discusses journals in the same field.

Statistics Study of the collection, analysis, interpretation, and presentation of data

Statistics is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.

Meta-analysis Statistical method that summarizes data from multiple sources

A meta-analysis is a statistical analysis that combines the results of multiple scientific studies. Meta-analysis can be performed when there are multiple scientific studies addressing the same question, with each individual study reporting measurements that are expected to have some degree of error. The aim then is to use approaches from statistics to derive a pooled estimate closest to the unknown common truth based on how this error is perceived.

Factor analysis is a statistical method used to describe variability among observed, correlated variables in terms of a potentially lower number of unobserved variables called factors. For example, it is possible that variations in six observed variables mainly reflect the variations in two unobserved (underlying) variables. Factor analysis searches for such joint variations in response to unobserved latent variables. The observed variables are modelled as linear combinations of the potential factors, plus "error" terms.

The g factor is a construct developed in psychometric investigations of cognitive abilities and human intelligence. It is a variable that summarizes positive correlations among different cognitive tasks, reflecting the fact that an individual's performance on one type of cognitive task tends to be comparable to that person's performance on other kinds of cognitive tasks. The g factor typically accounts for 40 to 50 percent of the between-individual performance differences on a given cognitive test, and composite scores based on many tests are frequently regarded as estimates of individuals' standing on the g factor. The terms IQ, general intelligence, general cognitive ability, general mental ability, and simply intelligence are often used interchangeably to refer to this common core shared by cognitive tests. The g factor targets a particular measure of general intelligence.

In statistics, an effect size is a number measuring the strength of the relationship between two variables in a population, or a sample-based estimate of that quantity. It can refer to the value of a statistic calculated from a sample of data, the value of a parameter for a hypothetical population, or to the equation that operationalizes how statistics or parameters lead to the effect size value. Examples of effect sizes include the correlation between two variables, the regression coefficient in a regression, the mean difference, or the risk of a particular event happening. Effect sizes complement statistical hypothesis testing, and play an important role in power analyses, sample size planning, and in meta-analyses. The cluster of data-analysis methods concerning effect sizes is referred to as estimation statistics.

Heteroscedasticity

In statistics, a vector of random variables is heteroscedastic if the variability of the random disturbance is different across elements of the vector. Here, variability could be quantified by the variance or any other measure of statistical dispersion. Thus heteroscedasticity is the absence of homoscedasticity. A typical example is the set of observations of income in different cities.

In statistics, multicollinearity is a phenomenon in which one predictor variable in a multiple regression model can be linearly predicted from the others with a substantial degree of accuracy. In this situation, the coefficient estimates of the multiple regression may change erratically in response to small changes in the model or the data. Multicollinearity does not reduce the predictive power or reliability of the model as a whole, at least within the sample data set; it only affects calculations regarding individual predictors. That is, a multivariate regression model with collinear predictors can indicate how well the entire bundle of predictors predicts the outcome variable, but it may not give valid results about any individual predictor, or about which predictors are redundant with respect to others.

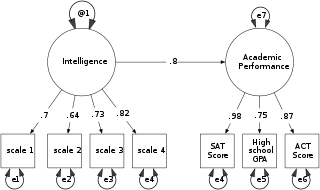
Structural equation modeling Form of causal modeling that fit networks of constructs to data

Structural equation modeling (SEM) includes a diverse set of mathematical models, computer algorithms, and statistical methods that fit networks of constructs to data. SEM includes confirmatory factor analysis, confirmatory composite analysis, path analysis, partial least squares path modeling, and latent growth modeling. The concept should not be confused with the related concept of structural models in econometrics, nor with structural models in economics. Structural equation models are often used to assess unobservable 'latent' constructs. They often invoke a measurement model that defines latent variables using one or more observed variables, and a structural model that imputes relationships between latent variables. The links between constructs of a structural equation model may be estimated with independent regression equations or through more involved approaches such as those employed in LISREL.

In psychology, discriminant validity tests whether concepts or measurements that are not supposed to be related are actually unrelated.

Acquiescence bias, also known as agreement bias, is a category of response bias common to survey research in which respondents have a tendency to select a positive response option or indicate a positive connotation disproportionately more frequently. Respondents do so without considering the content of the question or their 'true' preference. Acquiescence is sometimes referred to as "yea-saying" and is the tendency of a respondent to agree with a statement when in doubt. Questions affected by acquiescence bias take the following format: a stimulus in the form of a statement is presented, followed by 'agree/disagree,' 'yes/no' or 'true/false' response options. For example, a respondent might be presented with the statement "gardening makes me feel happy," and would then be expected to select either 'agree' or 'disagree.' Such question formats are favoured by both survey designers and respondents because they are straightforward to produce and respond to. The bias is particularly prevalent in the case of surveys or questionnaires that employ truisms as the stimuli, such as: "It is better to give than to receive" or "Never a lender nor a borrower be". Acquiescence bias can introduce systematic errors that affect the validity of research by confounding attitudes and behaviours with the general tendency to agree, which can result in misguided inference. Research suggests that the proportion of respondents who carry out this behaviour is between 10% and 20%.

In statistics, confirmatory factor analysis (CFA) is a special form of factor analysis, most commonly used in social research. It is used to test whether measures of a construct are consistent with a researcher's understanding of the nature of that construct. As such, the objective of confirmatory factor analysis is to test whether the data fit a hypothesized measurement model. This hypothesized model is based on theory and/or previous analytic research. CFA was first developed by Jöreskog (1969) and has built upon and replaced older methods of analyzing construct validity such as the MTMM Matrix as described in Campbell & Fiske (1959).

Statistical conclusion validity is the degree to which conclusions about the relationship among variables based on the data are correct or "reasonable". This began as being solely about whether the statistical conclusion about the relationship of the variables was correct, but now there is a movement towards moving to "reasonable" conclusions that use: quantitative, statistical, and qualitative data. Fundamentally, two types of errors can occur: type I and type II. Statistical conclusion validity concerns the qualities of the study that make these types of errors more likely. Statistical conclusion validity involves ensuring the use of adequate sampling procedures, appropriate statistical tests, and reliable measurement procedures.

In multivariate statistics, exploratory factor analysis (EFA) is a statistical method used to uncover the underlying structure of a relatively large set of variables. EFA is a technique within factor analysis whose overarching goal is to identify the underlying relationships between measured variables. It is commonly used by researchers when developing a scale and serves to identify a set of latent constructs underlying a battery of measured variables. It should be used when the researcher has no a priori hypothesis about factors or patterns of measured variables. Measured variables are any one of several attributes of people that may be observed and measured. Examples of measured variables could be the physical height, weight, and pulse rate of a human being. Usually, researchers would have a large number of measured variables, which are assumed to be related to a smaller number of "unobserved" factors. Researchers must carefully consider the number of measured variables to include in the analysis. EFA procedures are more accurate when each factor is represented by multiple measured variables in the analysis.

Substitutes for leadership theory is a leadership theory first developed by Steven Kerr and John M. Jermier and published in Organizational Behavior and Human Performance in December 1978.

Measurement invariance or measurement equivalence is a statistical property of measurement that indicates that the same construct is being measured across some specified groups. For example, measurement invariance can be used to study whether a given measure is interpreted in a conceptually similar manner by respondents representing different genders or cultural backgrounds. Violations of measurement invariance may preclude meaningful interpretation of measurement data. Tests of measurement invariance are increasingly used in fields such as psychology to supplement evaluation of measurement quality rooted in classical test theory.

Philip Michael Podsakoff is an American management professor, researcher, author, and consultant who held the John F. Mee Chair of Management at Indiana University. Currently, he is the Hyatt and Cici Brown Chair in Business at the University of Florida.

The partial least squares path modeling or partial least squares structural equation modeling is a method of structural equation modeling which allows estimating complex cause-effect relationship models with latent variables.

WarpPLS

WarpPLS is a software with graphical user interface for variance-based and factor-based structural equation modeling (SEM) using the partial least squares and factor-based methods. The software can be used in empirical research to analyse collected data and test hypothesized relationships. Since it runs on the MATLAB Compiler Runtime, it does not require the MATLAB software development application to be installed; and can be installed and used on various operating systems in addition to Windows, with virtual installations.

In statistics, confirmatory composite analysis (CCA) is a sub-type of structural equation modeling (SEM). Although, historically, CCA emerged from a re-orientation and re-start of partial least squares path modeling (PLS-PM), it has become an independent approach and the two should not be confused. In many ways it is similar to, but also quite distinct from confirmatory factor analysis (CFA). It shares with CFA the process of model specification, model identification, model estimation, and model assessment. However, in contrast to CFA which always assumes the existence of latent variables, in CCA all variables can be observable, with their interrelationships expressed in terms of composites, i.e., linear compounds of subsets of the variables. The composites are treated as the fundamental objects and path diagrams can be used to illustrate their relationships. This makes CCA particularly useful for disciplines examining theoretical concepts that are designed to attain certain goals, so-called artifacts, and their interplay with theoretical concepts of behavioral sciences.

References

  1. 1 2 Podsakoff, P.M.; MacKenzie, S.B.; Lee, J.-Y.; Podsakoff, N.P. (October 2003). "Common method biases in behavioral research: A critical review of the literature and recommended remedies" (PDF). Journal of Applied Psychology. 88 (5): 879–903. doi:10.1037/0021-9010.88.5.879. hdl: 2027.42/147112 . PMID   14516251.
  2. 1 2 Richardson, H.A.; Simmering, M.J.; Sturman, M.C. (October 2009). "A tale of three perspectives: Examining post hoc statistical techniques for detection and correction of common method variance". Organizational Research Methods. 12 (4): 762–800. doi:10.1177/1094428109332834. hdl: 1813/72364 .
  3. ↑ Williams, L. J.; Brown, B. K. (1994). "Method variance in organizational behavior and human resources research: Effects on correlations, path coefficients, and hypothesis testing". Organizational Behavior and Human Decision Processes. 57 (2): 185–209. doi:10.1006/obhd.1994.1011.
  4. ↑ Spector, P. E. (2006). "Method Variance in Organizational Research: Truth or Urban Legend?". Organizational Research Methods. 9 (2): 221–232. doi:10.1177/1094428105284955.
  5. ↑ Chang, S.-J.; van Witteloostuijn, A.; Eden, L. (2010). "Common method variance in international business research". Journal of International Business Studies. 41: 178–184. doi: 10.1057/jibs.2009.88 .
  6. ↑ Lindell, M. K.; Whitney, D. J. (2001). "Accounting for common method variance in cross-sectional research designs". Journal of Applied Psychology. 86 (1): 114–121. doi:10.1037/0021-9010.86.1.114.
  7. ↑ Williams, L.J.; Hartman, N.; Cavazotte, F. (July 2010). "Method variance and marker variables: A review and comprehensive CFA marker technique". Organizational Research Methods. 13 (3): 477–514. doi:10.1177/1094428110366036.
  8. ↑ Kock, N. (2015). Common method bias in PLS-SEM: A full collinearity assessment approach. International Journal of e-Collaboration, 11(4), 1-10.
  9. ↑ Kock, N.; Lynn, G. S. (2012). "Lateral collinearity and misleading results in variance-based SEM: An illustration and recommendations" (PDF). Journal of the Association for Information Systems. 13 (7): 546–580. doi:10.17705/1jais.00302.


Bellcurve.svg

This statistics-related article is a stub. You can help Wikipedia by expanding it.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.