
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is helpful in many branches of mathematics, including algebraic geometry, number theory, analytic combinatorics, and applied mathematics, as well as in physics, including the branches of hydrodynamics, thermodynamics, quantum mechanics, and twistor theory. By extension, use of complex analysis also has applications in engineering fields such as nuclear, aerospace, mechanical and electrical engineering.

In mathematics, specifically general topology, compactness is a property that seeks to generalize the notion of a closed and bounded subset of Euclidean space. The idea is that a compact space has no "punctures" or "missing endpoints", i.e., it includes all limiting values of points. For example, the open interval (0,1) would not be compact because it excludes the limiting values of 0 and 1, whereas the closed interval [0,1] would be compact. Similarly, the space of rational numbers is not compact, because it has infinitely many "punctures" corresponding to the irrational numbers, and the space of real numbers is not compact either, because it excludes the two limiting values and . However, the extended real number linewould be compact, since it contains both infinities. There are many ways to make this heuristic notion precise. These ways usually agree in a metric space, but may not be equivalent in other topological spaces.
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of unintuitive properties. It was discovered in 1874 by Henry John Stephen Smith and mentioned by German mathematician Georg Cantor in 1883.

In mathematics, computable numbers are the real numbers that can be computed to within any desired precision by a finite, terminating algorithm. They are also known as the recursive numbers, effective numbers or the computable reals or recursive reals. The concept of a computable real number was introduced by Emile Borel in 1912, using the intuitive notion of computability available at the time.
In mathematics, the branch of real analysis studies the behavior of real numbers, sequences and series of real numbers, and real functions. Some particular properties of real-valued sequences and functions that real analysis studies include convergence, limits, continuity, smoothness, differentiability and integrability.

In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members. The number of elements is called the length of the sequence. Unlike a set, the same elements can appear multiple times at different positions in a sequence, and unlike a set, the order does matter. Formally, a sequence can be defined as a function from natural numbers to the elements at each position. The notion of a sequence can be generalized to an indexed family, defined as a function from an arbitrary index set.
In mathematics, a topological space is called separable if it contains a countable, dense subset; that is, there exists a sequence of elements of the space such that every nonempty open subset of the space contains at least one element of the sequence.
In mathematical analysis, the Haar measure assigns an "invariant volume" to subsets of locally compact topological groups, consequently defining an integral for functions on those groups.

Cantor's diagonal argument is a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence with the infinite set of natural numbers – informally, that there are sets which in some sense contain more elements than there are positive integers. Such sets are now called uncountable sets, and the size of infinite sets is treated by the theory of cardinal numbers, which Cantor began.
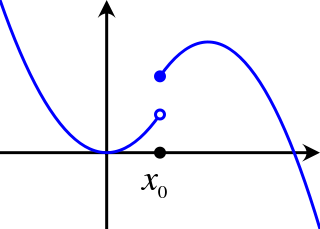
In mathematical analysis, semicontinuity is a property of extended real-valued functions that is weaker than continuity. An extended real-valued function is uppersemicontinuous at a point if, roughly speaking, the function values for arguments near are not much higher than
In mathematics, constructive analysis is mathematical analysis done according to some principles of constructive mathematics.
In computability theory, a set S of natural numbers is called computably enumerable (c.e.), recursively enumerable (r.e.), semidecidable, partially decidable, listable, provable or Turing-recognizable if:
In mathematics, the Gelfand representation in functional analysis is either of two things:

In mathematics, Pontryagin duality is a duality between locally compact abelian groups that allows generalizing Fourier transform to all such groups, which include the circle group, the finite abelian groups, and the additive group of the integers, the real numbers, and every finite-dimensional vector space over the reals or a p-adic field.
In mathematics, the support of a real-valued function is the subset of the function domain containing the elements which are not mapped to zero. If the domain of is a topological space, then the support of is instead defined as the smallest closed set containing all points not mapped to zero. This concept is used widely in mathematical analysis.
In several mathematical areas, including harmonic analysis, topology, and number theory, locally compact abelian groups are abelian groups which have a particularly convenient topology on them. For example, the group of integers, or the real numbers or the circle are locally compact abelian groups.
In mathematics, a Radon measure, named after Johann Radon, is a measure on the σ-algebra of Borel sets of a Hausdorff topological space X that is finite on all compact sets, outer regular on all Borel sets, and inner regular on open sets. These conditions guarantee that the measure is "compatible" with the topology of the space, and most measures used in mathematical analysis and in number theory are indeed Radon measures.
Computable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithms, in the sense that a function is computable if there exists an algorithm that can do the job of the function, i.e. given an input of the function domain it can return the corresponding output. Computable functions are used to discuss computability without referring to any concrete model of computation such as Turing machines or register machines. Any definition, however, must make reference to some specific model of computation but all valid definitions yield the same class of functions. Particular models of computability that give rise to the set of computable functions are the Turing-computable functions and the general recursive functions.
In computability theory, hyperarithmetic theory is a generalization of Turing computability. It has close connections with definability in second-order arithmetic and with weak systems of set theory such as Kripke–Platek set theory. It is an important tool in effective descriptive set theory.

In mathematics, a real number is a number that can be used to measure a continuous one-dimensional quantity such as a distance, duration or temperature. Here, continuous means that pairs of values can have arbitrarily small differences. Every real number can be almost uniquely represented by an infinite decimal expansion.





























