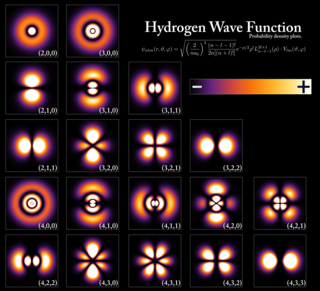
In atomic theory and quantum mechanics, an atomic orbital is a function describing the location and wave-like behavior of an electron in an atom. This function can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus. The term atomic orbital may also refer to the physical region or space where the electron can be calculated to be present, as predicted by the particular mathematical form of the orbital.
A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral atom contains a single positively charged proton and a single negatively charged electron bound to the nucleus by the Coulomb force. Atomic hydrogen constitutes about 75% of the baryonic mass of the universe.

A quantum mechanical system or particle that is bound—that is, confined spatially—can only take on certain discrete values of energy, called energy levels. This contrasts with classical particles, which can have any amount of energy. The term is commonly used for the energy levels of the electrons in atoms, ions, or molecules, which are bound by the electric field of the nucleus, but can also refer to energy levels of nuclei or vibrational or rotational energy levels in molecules. The energy spectrum of a system with such discrete energy levels is said to be quantized.
In quantum mechanics, the case of a particle in a one-dimensional ring is similar to the particle in a box. The Schrödinger equation for a free particle which is restricted to a ring is

In atomic physics, hyperfine structure is defined by small shifts in otherwise degenerate energy levels and the resulting splittings in those energy levels of atoms, molecules, and ions, due to electromagnetic multipole interaction between the nucleus and electron clouds.
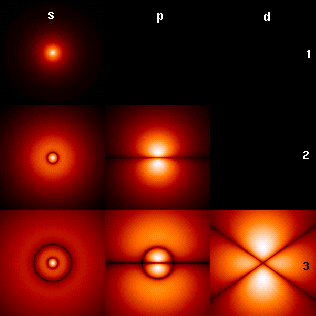
In quantum mechanics, the azimuthal quantum number is a quantum number for an atomic orbital that determines its orbital angular momentum and describes the shape of the orbital. The azimuthal quantum number is the second of a set of quantum numbers that describe the unique quantum state of an electron. It is also known as the orbital angular momentum quantum number, orbital quantum number, subsidiary quantum number, or second quantum number, and is symbolized as ℓ.
In atomic physics, a magnetic quantum number is a quantum number used to distinguish quantum states of an electron or other particle according to its angular momentum along a given axis in space. The orbital magnetic quantum number distinguishes the orbitals available within a given subshell of an atom. It specifies the component of the orbital angular momentum that lies along a given axis, conventionally called the z-axis, so it describes the orientation of the orbital in space. The spin magnetic quantum numberms specifies the z-axis component of the spin angular momentum for a particle having spin quantum number s. For an electron, s is 1⁄2, and ms is either +1⁄2 or −1⁄2, often called "spin-up" and "spin-down", or α and β. The term magnetic in the name refers to the magnetic dipole moment associated with each type of angular momentum, so states having different magnetic quantum numbers shift in energy in a magnetic field according to the Zeeman effect.
In physics and chemistry, a selection rule, or transition rule, formally constrains the possible transitions of a system from one quantum state to another. Selection rules have been derived for electromagnetic transitions in molecules, in atoms, in atomic nuclei, and so on. The selection rules may differ according to the technique used to observe the transition. The selection rule also plays a role in chemical reactions, where some are formally spin-forbidden reactions, that is, reactions where the spin state changes at least once from reactants to products.
In physics, the C parity or charge parity is a multiplicative quantum number of some particles that describes their behavior under the symmetry operation of charge conjugation.
In molecular physics, the molecular term symbol is a shorthand expression of the group representation and angular momenta that characterize the state of a molecule, i.e. its electronic quantum state which is an eigenstate of the electronic molecular Hamiltonian. It is the equivalent of the term symbol for the atomic case. However, the following presentation is restricted to the case of homonuclear diatomic molecules, or other symmetric molecules with an inversion centre. For heteronuclear diatomic molecules, the u/g symbol does not correspond to any exact symmetry of the electronic molecular Hamiltonian. In the case of less symmetric molecules the molecular term symbol contains the symbol of the group representation to which the molecular electronic state belongs.
Multi-configurational self-consistent field (MCSCF) is a method in quantum chemistry used to generate qualitatively correct reference states of molecules in cases where Hartree–Fock and density functional theory are not adequate. It uses a linear combination of configuration state functions (CSF), or configuration determinants, to approximate the exact electronic wavefunction of an atom or molecule. In an MCSCF calculation, the set of coefficients of both the CSFs or determinants and the basis functions in the molecular orbitals are varied to obtain the total electronic wavefunction with the lowest possible energy. This method can be considered a combination between configuration interaction and Hartree–Fock.
A stationary state is a quantum state with all observables independent of time. It is an eigenvector of the energy operator. It is also called energy eigenvector, energy eigenstate, energy eigenfunction, or energy eigenket. It is very similar to the concept of atomic orbital and molecular orbital in chemistry, with some slight differences explained below.
The theoretical and experimental justification for the Schrödinger equation motivates the discovery of the Schrödinger equation, the equation that describes the dynamics of nonrelativistic particles. The motivation uses photons, which are relativistic particles with dynamics described by Maxwell's equations, as an analogue for all types of particles.
In atomic, molecular, and optical physics and quantum chemistry, the molecular Hamiltonian is the Hamiltonian operator representing the energy of the electrons and nuclei in a molecule. This operator and the associated Schrödinger equation play a central role in computational chemistry and physics for computing properties of molecules and aggregates of molecules, such as thermal conductivity, specific heat, electrical conductivity, optical, and magnetic properties, and reactivity.
A hydrogen-like atom (or hydrogenic atom) is any atom or ion with a single valence electron. These atoms are isoelectronic with hydrogen. Examples of hydrogen-like atoms include, but are not limited to, hydrogen itself, all alkali metals such as Rb and Cs, singly ionized alkaline earth metals such as Ca+ and Sr+ and other ions such as He+, Li2+, and Be3+ and isotopes of any of the above. A hydrogen-like atom includes a positively charged core consisting of the atomic nucleus and any core electrons as well as a single valence electron. Because helium is common in the universe, the spectroscopy of singly ionized helium is important in EUV astronomy, for example, of DO white dwarf stars.
In 1927, a year after the publication of the Schrödinger equation, Hartree formulated what are now known as the Hartree equations for atoms, using the concept of self-consistency that Lindsay had introduced in his study of many electron systems in the context of Bohr theory. Hartree assumed that the nucleus together with the electrons formed a spherically symmetric field. The charge distribution of each electron was the solution of the Schrödinger equation for an electron in a potential , derived from the field. Self-consistency required that the final field, computed from the solutions, was self-consistent with the initial field, and he thus called his method the self-consistent field method.
Within computational chemistry, the Slater–Condon rules express integrals of one- and two-body operators over wavefunctions constructed as Slater determinants of orthonormal orbitals in terms of the individual orbitals. In doing so, the original integrals involving N-electron wavefunctions are reduced to sums over integrals involving at most two molecular orbitals, or in other words, the original 3N dimensional integral is expressed in terms of many three- and six-dimensional integrals.
A helium atom is an atom of the chemical element helium. Helium is composed of two electrons bound by the electromagnetic force to a nucleus containing two protons along with either one or two neutrons, depending on the isotope, held together by the strong force. Unlike for hydrogen, a closed-form solution to the Schrödinger equation for the helium atom has not been found. However, various approximations, such as the Hartree–Fock method, can be used to estimate the ground state energy and wavefunction of the atom.
In rotational-vibrational and electronic spectroscopy of diatomic molecules, Hund's coupling cases are idealized descriptions of rotational states in which specific terms in the molecular Hamiltonian and involving couplings between angular momenta are assumed to dominate over all other terms. There are five cases, proposed by Friedrich Hund in 1926-27 and traditionally denoted by the letters (a) through (e). Most diatomic molecules are somewhere between the idealized cases (a) and (b).
In pure and applied mathematics, quantum mechanics and computer graphics, a tensor operator generalizes the notion of operators which are scalars and vectors. A special class of these are spherical tensor operators which apply the notion of the spherical basis and spherical harmonics. The spherical basis closely relates to the description of angular momentum in quantum mechanics and spherical harmonic functions. The coordinate-free generalization of a tensor operator is known as a representation operator.
























































