
In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. In its integral form, it states that the flux of the electric field out of an arbitrary closed surface is proportional to the electric charge enclosed by the surface, irrespective of how that charge is distributed. Even though the law alone is insufficient to determine the electric field across a surface enclosing any charge distribution, this may be possible in cases where symmetry mandates uniformity of the field. Where no such symmetry exists, Gauss's law can be used in its differential form, which states that the divergence of the electric field is proportional to the local density of charge.
In physics, the screened Poisson equation is a Poisson equation, which arises in the Klein–Gordon equation, electric field screening in plasmas, and nonlocal granular fluidity in granular flow.

Poisson's equation is an elliptic partial differential equation of broad utility in theoretical physics. For example, the solution to Poisson's equation is the potential field caused by a given electric charge or mass density distribution; with the potential field known, one can then calculate electrostatic or gravitational (force) field. It is a generalization of Laplace's equation, which is also frequently seen in physics. The equation is named after French mathematician and physicist Siméon Denis Poisson.
In the calculus of variations, a field of mathematical analysis, the functional derivative relates a change in a functional to a change in a function on which the functional depends.

Electrostatics is a branch of physics that studies slow-moving or stationary electric charges.
In quantum physics, Fermi's golden rule is a formula that describes the transition rate from one energy eigenstate of a quantum system to a group of energy eigenstates in a continuum, as a result of a weak perturbation. This transition rate is effectively independent of time and is proportional to the strength of the coupling between the initial and final states of the system as well as the density of states. It is also applicable when the final state is discrete, i.e. it is not part of a continuum, if there is some decoherence in the process, like relaxation or collision of the atoms, or like noise in the perturbation, in which case the density of states is replaced by the reciprocal of the decoherence bandwidth.
In plasmas and electrolytes, the Debye length, is a measure of a charge carrier's net electrostatic effect in a solution and how far its electrostatic effect persists. With each Debye length the charges are increasingly electrically screened and the electric potential decreases in magnitude by 1/e. A Debye sphere is a volume whose radius is the Debye length. Debye length is an important parameter in plasma physics, electrolytes, and colloids. The corresponding Debye screening wave vector for particles of density , charge at a temperature is given by in Gaussian units. Expressions in MKS units will be given below. The analogous quantities at very low temperatures are known as the Thomas–Fermi length and the Thomas–Fermi wave vector. They are of interest in describing the behaviour of electrons in metals at room temperature.

Electric potential energy is a potential energy that results from conservative Coulomb forces and is associated with the configuration of a particular set of point charges within a defined system. An object may be said to have electric potential energy by virtue of either its own electric charge or its relative position to other electrically charged objects.
The Vlasov equation is a differential equation describing time evolution of the distribution function of plasma consisting of charged particles with long-range interaction, such as the Coulomb interaction. The equation was first suggested for the description of plasma by Anatoly Vlasov in 1938 and later discussed by him in detail in a monograph.
In physics, the Einstein relation is a previously unexpected connection revealed independently by William Sutherland in 1904, Albert Einstein in 1905, and by Marian Smoluchowski in 1906 in their works on Brownian motion. The more general form of the equation in the classical case is

In electromagnetism, charge density is the amount of electric charge per unit length, surface area, or volume. Volume charge density is the quantity of charge per unit volume, measured in the SI system in coulombs per cubic meter (C⋅m−3), at any point in a volume. Surface charge density (σ) is the quantity of charge per unit area, measured in coulombs per square meter (C⋅m−2), at any point on a surface charge distribution on a two dimensional surface. Linear charge density (λ) is the quantity of charge per unit length, measured in coulombs per meter (C⋅m−1), at any point on a line charge distribution. Charge density can be either positive or negative, since electric charge can be either positive or negative.
Local-density approximations (LDA) are a class of approximations to the exchange–correlation (XC) energy functional in density functional theory (DFT) that depend solely upon the value of the electronic density at each point in space. Many approaches can yield local approximations to the XC energy. However, overwhelmingly successful local approximations are those that have been derived from the homogeneous electron gas (HEG) model. In this regard, LDA is generally synonymous with functionals based on the HEG approximation, which are then applied to realistic systems.
The Kohn-Sham equations are a set of mathematical equations used in quantum mechanics to simplify the complex problem of understanding how electrons behave in atoms and molecules. They introduce fictitious non-interacting electrons and use them to find the most stable arrangement of electrons, which helps scientists understand and predict the properties of matter at the atomic and molecular scale.
The Poisson–Boltzmann equation is a useful equation in many settings, whether it be to understand physiological interfaces, polymer science, electron interactions in a semiconductor, or more. It aims to describe the distribution of the electric potential in solution in the direction normal to a charged surface. This distribution is important to determine how the electrostatic interactions will affect the molecules in solution. The Poisson–Boltzmann equation is derived via mean-field assumptions. From the Poisson–Boltzmann equation many other equations have been derived with a number of different assumptions.
In atomic, molecular, and optical physics and quantum chemistry, the molecular Hamiltonian is the Hamiltonian operator representing the energy of the electrons and nuclei in a molecule. This operator and the associated Schrödinger equation play a central role in computational chemistry and physics for computing properties of molecules and aggregates of molecules, such as thermal conductivity, specific heat, electrical conductivity, optical, and magnetic properties, and reactivity.

There are various mathematical descriptions of the electromagnetic field that are used in the study of electromagnetism, one of the four fundamental interactions of nature. In this article, several approaches are discussed, although the equations are in terms of electric and magnetic fields, potentials, and charges with currents, generally speaking.
Defect types include atom vacancies, adatoms, steps, and kinks that occur most frequently at surfaces due to the finite material size causing crystal discontinuity. What all types of defects have in common, whether surface or bulk defects, is that they produce dangling bonds that have specific electron energy levels different from those of the bulk. This difference occurs because these states cannot be described with periodic Bloch waves due to the change in electron potential energy caused by the missing ion cores just outside the surface. Hence, these are localized states that require separate solutions to the Schrödinger equation so that electron energies can be properly described. The break in periodicity results in a decrease in conductivity due to defect scattering.
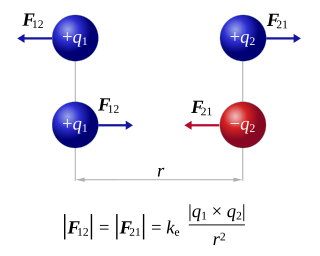
Coulomb's inverse-square law, or simply Coulomb's law, is an experimental law of physics that calculates the amount of force between two electrically charged particles at rest. This electric force is conventionally called electrostatic force or Coulomb force. Although the law was known earlier, it was first published in 1785 by French physicist Charles-Augustin de Coulomb. Coulomb's law was essential to the development of the theory of electromagnetism and maybe even its starting point, as it allowed meaningful discussions of the amount of electric charge in a particle.
Static force fields are fields, such as a simple electric, magnetic or gravitational fields, that exist without excitations. The most common approximation method that physicists use for scattering calculations can be interpreted as static forces arising from the interactions between two bodies mediated by virtual particles, particles that exist for only a short time determined by the uncertainty principle. The virtual particles, also known as force carriers, are bosons, with different bosons associated with each force.

The electric dipole moment is a measure of the separation of positive and negative electrical charges within a system, that is, a measure of the system's overall polarity. The SI unit for electric dipole moment is the coulomb-meter (C⋅m). The debye (D) is another unit of measurement used in atomic physics and chemistry.



























