
Bandwidth is the difference between the upper and lower frequencies in a continuous band of frequencies. It is typically measured in hertz, and depending on context, may specifically refer to passband bandwidth or baseband bandwidth. Passband bandwidth is the difference between the upper and lower cutoff frequencies of, for example, a band-pass filter, a communication channel, or a signal spectrum. Baseband bandwidth applies to a low-pass filter or baseband signal; the bandwidth is equal to its upper cutoff frequency.

In mathematics, the geometric mean is a mean or average which indicates a central tendency of a finite set of real numbers by using the product of their values. The geometric mean is defined as the nth root of the product of n numbers, i.e., for a set of numbers a1, a2, ..., an, the geometric mean is defined as
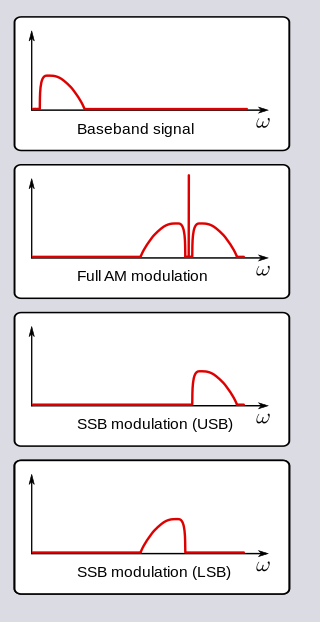
In radio communications, single-sideband modulation (SSB) or single-sideband suppressed-carrier modulation (SSB-SC) is a type of modulation used to transmit information, such as an audio signal, by radio waves. A refinement of amplitude modulation, it uses transmitter power and bandwidth more efficiently. Amplitude modulation produces an output signal the bandwidth of which is twice the maximum frequency of the original baseband signal. Single-sideband modulation avoids this bandwidth increase, and the power wasted on a carrier, at the cost of increased device complexity and more difficult tuning at the receiver.

The Nyquist–Shannon sampling theorem is an essential principle for digital signal processing linking the frequency range of a signal and the sample rate required to avoid a type of distortion called aliasing. The theorem states that the sample rate must be at least twice the bandwidth of the signal to avoid aliasing distortion. In practice, it is used to select band-limiting filters to keep aliasing distortion below an acceptable amount when an analog signal is sampled or when sample rates are changed within a digital signal processing function.
Signal-to-noise ratio is a measure used in science and engineering that compares the level of a desired signal to the level of background noise. SNR is defined as the ratio of signal power to noise power, often expressed in decibels. A ratio higher than 1:1 indicates more signal than noise.

The mel scale is a perceptual scale of pitches judged by listeners to be equal in distance from one another. The reference point between this scale and normal frequency measurement is defined by assigning a perceptual pitch of 1000 mels to a 1000 Hz tone, 40 dB above the listener's threshold. Above about 500 Hz, increasingly large intervals are judged by listeners to produce equal pitch increments.
In information theory, the Shannon–Hartley theorem tells the maximum rate at which information can be transmitted over a communications channel of a specified bandwidth in the presence of noise. It is an application of the noisy-channel coding theorem to the archetypal case of a continuous-time analog communications channel subject to Gaussian noise. The theorem establishes Shannon's channel capacity for such a communication link, a bound on the maximum amount of error-free information per time unit that can be transmitted with a specified bandwidth in the presence of the noise interference, assuming that the signal power is bounded, and that the Gaussian noise process is characterized by a known power or power spectral density. The law is named after Claude Shannon and Ralph Hartley.

In mathematics, Stirling's approximation is an approximation for factorials. It is a good approximation, leading to accurate results even for small values of . It is named after James Stirling, though a related but less precise result was first stated by Abraham de Moivre.
The jansky is a non-SI unit of spectral flux density, or spectral irradiance, used especially in radio astronomy. It is equivalent to 10−26 watts per square metre per hertz.
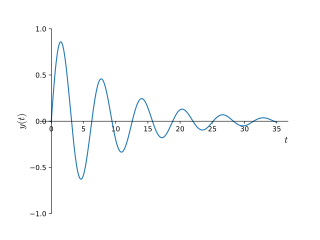
In physics and engineering, the quality factor or Q factor is a dimensionless parameter that describes how underdamped an oscillator or resonator is. It is defined as the ratio of the initial energy stored in the resonator to the energy lost in one radian of the cycle of oscillation. Q factor is alternatively defined as the ratio of a resonator's centre frequency to its bandwidth when subject to an oscillating driving force. These two definitions give numerically similar, but not identical, results. Higher Q indicates a lower rate of energy loss and the oscillations die out more slowly. A pendulum suspended from a high-quality bearing, oscillating in air, has a high Q, while a pendulum immersed in oil has a low one. Resonators with high quality factors have low damping, so that they ring or vibrate longer.
Chebyshev filters are analog or digital filters that have a steeper roll-off than Butterworth filters, and have either passband ripple or stopband ripple. Chebyshev filters have the property that they minimize the error between the idealized and the actual filter characteristic over the operating frequency range of the filter, but they achieve this with ripples in the passband. This type of filter is named after Pafnuty Chebyshev because its mathematical characteristics are derived from Chebyshev polynomials. Type I Chebyshev filters are usually referred to as "Chebyshev filters", while type II filters are usually called "inverse Chebyshev filters". Because of the passband ripple inherent in Chebyshev filters, filters with a smoother response in the passband but a more irregular response in the stopband are preferred for certain applications.
Sound power or acoustic power is the rate at which sound energy is emitted, reflected, transmitted or received, per unit time. It is defined as "through a surface, the product of the sound pressure, and the component of the particle velocity, at a point on the surface in the direction normal to the surface, integrated over that surface." The SI unit of sound power is the watt (W). It relates to the power of the sound force on a surface enclosing a sound source, in air. For a sound source, unlike sound pressure, sound power is neither room-dependent nor distance-dependent. Sound pressure is a property of the field at a point in space, while sound power is a property of a sound source, equal to the total power emitted by that source in all directions. Sound power passing through an area is sometimes called sound flux or acoustic flux through that area.
In electronics, when describing a voltage or current step function, rise time is the time taken by a signal to change from a specified low value to a specified high value. These values may be expressed as ratios or, equivalently, as percentages with respect to a given reference value. In analog electronics and digital electronics, these percentages are commonly the 10% and 90% of the output step height: however, other values are commonly used. For applications in control theory, according to Levine, rise time is defined as "the time required for the response to rise from x% to y% of its final value", with 0% to 100% rise time common for underdamped second order systems, 5% to 95% for critically damped and 10% to 90% for overdamped ones. According to Orwiler, the term "rise time" applies to either positive or negative step response, even if a displayed negative excursion is popularly termed fall time.
In audiology and psychoacoustics the concept of critical bands, introduced by Harvey Fletcher in 1933 and refined in 1940, describes the frequency bandwidth of the "auditory filter" created by the cochlea, the sense organ of hearing within the inner ear. Roughly, the critical band is the band of audio frequencies within which a second tone will interfere with the perception of the first tone by auditory masking.

The gain–bandwidth product for an amplifier is the product of the amplifier's bandwidth and the gain at which the bandwidth is measured.
Ripple in electronics is the residual periodic variation of the DC voltage within a power supply which has been derived from an alternating current (AC) source. This ripple is due to incomplete suppression of the alternating waveform after rectification. Ripple voltage originates as the output of a rectifier or from generation and commutation of DC power.
The zero-order hold (ZOH) is a mathematical model of the practical signal reconstruction done by a conventional digital-to-analog converter (DAC). That is, it describes the effect of converting a discrete-time signal to a continuous-time signal by holding each sample value for one sample interval. It has several applications in electrical communication.

In electronics and signal processing, mainly in digital signal processing, a Gaussian filter is a filter whose impulse response is a Gaussian function. Gaussian filters have the properties of having no overshoot to a step function input while minimizing the rise and fall time. This behavior is closely connected to the fact that the Gaussian filter has the minimum possible group delay. A Gaussian filter will have the best combination of suppression of high frequencies while also minimizing spatial spread, being the critical point of the uncertainty principle. These properties are important in areas such as oscilloscopes and digital telecommunication systems.

In mathematics and signal processing, the constant-Q transform and variable-Q transform, simply known as CQT and VQT, transforms a data series to the frequency domain. It is related to the Fourier transform and very closely related to the complex Morlet wavelet transform. Its design is suited for musical representation.
In fluid dynamics, the Darcy friction factor formulae are equations that allow the calculation of the Darcy friction factor, a dimensionless quantity used in the Darcy–Weisbach equation, for the description of friction losses in pipe flow as well as open-channel flow.
















