
In physics, the Maxwell–Boltzmann distribution, or Maxwell(ian) distribution, is a particular probability distribution named after James Clerk Maxwell and Ludwig Boltzmann.

In mathematical physics, the Dirac delta distribution, also known as the unit impulse, is a generalized function or distribution over the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one.
In quantum computing, Grover's algorithm, also known as the quantum search algorithm, refers to a quantum algorithm for unstructured search that finds with high probability the unique input to a black box function that produces a particular output value, using just evaluations of the function, where is the size of the function's domain. It was devised by Lov Grover in 1996.

The kinetic theory of gases is a simple, historically significant classical model of the thermodynamic behavior of gases, with which many principal concepts of thermodynamics were established. The model describes a gas as a large number of identical submicroscopic particles, all of which are in constant, rapid, random motion. Their size is assumed to be much smaller than the average distance between the particles. The particles undergo random elastic collisions between themselves and with the enclosing walls of the container. The basic version of the model describes the ideal gas, and considers no other interactions between the particles.
In calculus, and more generally in mathematical analysis, integration by parts or partial integration is a process that finds the integral of a product of functions in terms of the integral of the product of their derivative and antiderivative. It is frequently used to transform the antiderivative of a product of functions into an antiderivative for which a solution can be more easily found. The rule can be thought of as an integral version of the product rule of differentiation.
In mechanics and geometry, the 3D rotation group, often denoted SO(3), is the group of all rotations about the origin of three-dimensional Euclidean space under the operation of composition.
In linear algebra, two vectors in an inner product space are orthonormal if they are orthogonal unit vectors. A set of vectors form an orthonormal set if all vectors in the set are mutually orthogonal and all of unit length. An orthonormal set which forms a basis is called an orthonormal basis.
In the mathematical field of differential geometry, a metric tensor is an additional structure on a manifold M that allows defining distances and angles, just as the inner product on a Euclidean space allows defining distances and angles there. More precisely, a metric tensor at a point p of M is a bilinear form defined on the tangent space at p, and a metric tensor on M consists of a metric tensor at each point p of M that varies smoothly with p.

In mathematics, the beta function, also called the Euler integral of the first kind, is a special function that is closely related to the gamma function and to binomial coefficients. It is defined by the integral
In differential geometry, the second fundamental form is a quadratic form on the tangent plane of a smooth surface in the three-dimensional Euclidean space, usually denoted by . Together with the first fundamental form, it serves to define extrinsic invariants of the surface, its principal curvatures. More generally, such a quadratic form is defined for a smooth immersed submanifold in a Riemannian manifold.
A fictitious force is a force that appears to act on a mass whose motion is described using a non-inertial frame of reference, such as a linearly accelerating or rotating reference frame. It is related to Newton's second law of motion, which treats forces for just one object.
A parametric surface is a surface in the Euclidean space which is defined by a parametric equation with two parameters :\mathbb {R} ^{2}\to \mathbb {R} ^{3}} . Parametric representation is a very general way to specify a surface, as well as implicit representation. Surfaces that occur in two of the main theorems of vector calculus, Stokes' theorem and the divergence theorem, are frequently given in a parametric form. The curvature and arc length of curves on the surface, surface area, differential geometric invariants such as the first and second fundamental forms, Gaussian, mean, and principal curvatures can all be computed from a given parametrization.
The Rabi problem concerns the response of an atom to an applied harmonic electric field, with an applied frequency very close to the atom's natural frequency. It provides a simple and generally solvable example of light–atom interactions and is named after Isidor Isaac Rabi.
Photon polarization is the quantum mechanical description of the classical polarized sinusoidal plane electromagnetic wave. An individual photon can be described as having right or left circular polarization, or a superposition of the two. Equivalently, a photon can be described as having horizontal or vertical linear polarization, or a superposition of the two.
In mathematics, the Möbius energy of a knot is a particular knot energy, i.e., a functional on the space of knots. It was discovered by Jun O'Hara, who demonstrated that the energy blows up as the knot's strands get close to one another. This is a useful property because it prevents self-intersection and ensures the result under gradient descent is of the same knot type.
This article derives the main properties of rotations in 3-dimensional space.
In probability theory and directional statistics, a circular uniform distribution is a probability distribution on the unit circle whose density is uniform for all angles.
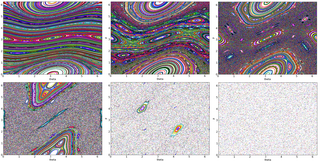
The kicked rotator, also spelled as kicked rotor, is a paradigmatic model for both Hamiltonian chaos and quantum chaos. It describes a free rotating stick in an inhomogeneous "gravitation like" field that is periodically switched on in short pulses. The model is described by the Hamiltonian
In NMR spectroscopy, the product operator formalism is a method used to determine the outcome of pulse sequences in a rigorous but straightforward way. With this method it is possible to predict how the bulk magnetization evolves with time under the action of pulses applied in different directions. It is a net improvement from the semi-classical vector model which is not able to predict many of the results in NMR spectroscopy and is a simplification of the complete density matrix formalism.
The problem of reconstructing a multidimensional signal from its projection is uniquely multidimensional, having no 1-D counterpart. It has applications that range from computer-aided tomography to geophysical signal processing. It is a problem which can be explored from several points of view—as a deconvolution problem, a modeling problem, an estimation problem, or an interpolation problem.




















