In mathematics, specifically number theory, Granville numbers, also known as -perfect numbers, are an extension of the perfect numbers.
In mathematics, specifically number theory, Granville numbers, also known as -perfect numbers, are an extension of the perfect numbers.
In 1996, Andrew Granville proposed the following construction of a set : [1]
A Granville number is an element of for which equality holds, that is, is a Granville number if it is equal to the sum of its proper divisors that are also in . Granville numbers are also called -perfect numbers. [2]
The elements of can be k-deficient, k-perfect, or k-abundant. In particular, 2-perfect numbers are a proper subset of . [1]
Numbers that fulfill the strict form of the inequality in the above definition are known as -deficient numbers. That is, the -deficient numbers are the natural numbers for which the sum of their divisors in is strictly less than themselves:
Numbers that fulfill equality in the above definition are known as -perfect numbers. [1] That is, the -perfect numbers are the natural numbers that are equal the sum of their divisors in . The first few -perfect numbers are:
Every perfect number is also -perfect. [1] However, there are numbers such as 24 which are -perfect but not perfect. The only known -perfect number with three distinct prime factors is 126 = 2 · 32 · 7. [2]
Every number of form 2^(n - 1) * (2^n - 1) * (2^n)^m where m >= 0, where 2^n - 1 is Prime, are Granville Numbers. So, there are infinitely many Granville Numbers and the infinite family has 2 prime factors- 2 and a Mersenne Prime. Others include 126, 5540590, 9078520, 22528935, 56918394 and 246650552 having 3, 5, 5, 5, 5 and 5 prime factors.
Numbers that violate the inequality in the above definition are known as -abundant numbers. That is, the -abundant numbers are the natural numbers for which the sum of their divisors in is strictly greater than themselves:
They belong to the complement of . The first few -abundant numbers are:
Every deficient number and every perfect number is in because the restriction of the divisors sum to members of either decreases the divisors sum or leaves it unchanged. The first natural number that is not in is the smallest abundant number, which is 12. The next two abundant numbers, 18 and 20, are also not in . However, the fourth abundant number, 24, is in because the sum of its proper divisors in is:
In other words, 24 is abundant but not -abundant because 12 is not in . In fact, 24 is -perfect - it is the smallest number that is -perfect but not perfect.
The smallest odd abundant number that is in is 2835, and the smallest pair of consecutive numbers that are not in are 5984 and 5985. [1]

Amicable numbers are two different natural numbers related in such a way that the sum of the proper divisors of each is equal to the other number. That is, s(a)=b and s(b)=a, where s(n)=σ(n)-n is equal to the sum of positive divisors of n except n itself (see also divisor function).
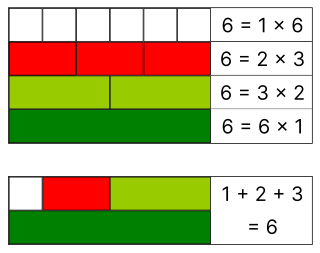
In number theory, a perfect number is a positive integer that is equal to the sum of its positive proper divisors, that is, divisors excluding the number itself. For instance, 6 has proper divisors 1, 2 and 3, and 1 + 2 + 3 = 6, so 6 is a perfect number. The next perfect number is 28, since 1 + 2 + 4 + 7 + 14 = 28.
2 (two) is a number, numeral and digit. It is the natural number following 1 and preceding 3. It is the smallest and only even prime number. Because it forms the basis of a duality, it has religious and spiritual significance in many cultures.

The tables below list all of the divisors of the numbers 1 to 1000.
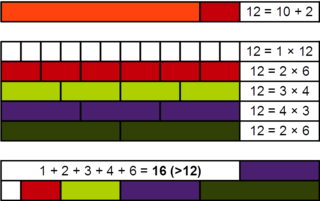
In number theory, an abundant number or excessive number is a positive integer for which the sum of its proper divisors is greater than the number. The integer 12 is the first abundant number. Its proper divisors are 1, 2, 3, 4 and 6 for a total of 16. The amount by which the sum exceeds the number is the abundance. The number 12 has an abundance of 4, for example.

In number theory, a deficient number or defective number is a positive integer n for which the sum of divisors of n is less than 2n. Equivalently, it is a number for which the sum of proper divisors is less than n. For example, the proper divisors of 8 are 1, 2, and 4, and their sum is less than 8, so 8 is deficient.

In number theory, a semiperfect number or pseudoperfect number is a natural number n that is equal to the sum of all or some of its proper divisors. A semiperfect number that is equal to the sum of all its proper divisors is a perfect number.

In number theory, a weird number is a natural number that is abundant but not semiperfect. In other words, the sum of the proper divisors of the number is greater than the number, but no subset of those divisors sums to the number itself.

In mathematics, an almost perfect number (sometimes also called slightly defective or least deficientnumber) is a natural number n such that the sum of all divisors of n (the sum-of-divisors function σ(n)) is equal to 2n − 1, the sum of all proper divisors of n, s(n) = σ(n) − n, then being equal to n − 1. The only known almost perfect numbers are powers of 2 with non-negative exponents (sequence A000079 in the OEIS). Therefore the only known odd almost perfect number is 20 = 1, and the only known even almost perfect numbers are those of the form 2k for some positive integer k; however, it has not been shown that all almost perfect numbers are of this form. It is known that an odd almost perfect number greater than 1 would have at least six prime factors.
90 (ninety) is the natural number following 89 and preceding 91.
72 (seventy-two) is the natural number following 71 and preceding 73. It is half a gross or 6 dozen.
96 (ninety-six) is the natural number following 95 and preceding 97. It is a number that appears the same when turned upside down.
1000 or one thousand is the natural number following 999 and preceding 1001. In most English-speaking countries, it can be written with or without a comma or sometimes a period separating the thousands digit: 1,000.

360 is the natural number following 359 and preceding 361.
126 is the natural number following 125 and preceding 127.
In number theory, friendly numbers are two or more natural numbers with a common abundancy index, the ratio between the sum of divisors of a number and the number itself. Two numbers with the same "abundancy" form a friendly pair; n numbers with the same "abundancy" form a friendly n-tuple.
1728 is the natural number following 1727 and preceding 1729. It is a dozen gross, or one great gross. It is also the number of cubic inches in a cubic foot.
5 (five) is a number, numeral and digit. It is the natural number, and cardinal number, following 4 and preceding 6, and is a prime number. It has garnered attention throughout history in part because distal extremities in humans typically contain five digits.
In number theory, the aliquot sums(n) of a positive integer n is the sum of all proper divisors of n, that is, all divisors of n other than n itself. That is,

In mathematics a primitive abundant number is an abundant number whose proper divisors are all deficient numbers.