In mathematics, specifically category theory, a functor is a mapping between categories. Functors were first considered in algebraic topology, where algebraic objects are associated to topological spaces, and maps between these algebraic objects are associated to continuous maps between spaces. Nowadays, functors are used throughout modern mathematics to relate various categories. Thus, functors are important in all areas within mathematics to which category theory is applied.
In mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:
In category theory, a branch of mathematics, a Grothendieck topology is a structure on a category C that makes the objects of C act like the open sets of a topological space. A category together with a choice of Grothendieck topology is called a site.
In algebra, a homomorphism is a structure-preserving map between two algebraic structures of the same type. The word homomorphism comes from the Ancient Greek language: ὁμός meaning "same" and μορφή meaning "form" or "shape". However, the word was apparently introduced to mathematics due to a (mis)translation of German ähnlich meaning "similar" to ὁμός meaning "same". The term "homomorphism" appeared as early as 1892, when it was attributed to the German mathematician Felix Klein (1849–1925).

In abstract algebra, a branch of mathematics, a monoid is a set equipped with an associative binary operation and an identity element. For example, the nonnegative integers with addition form a monoid, the identity element being 0.
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties.

In mathematics, a category is a collection of "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose objects are sets and whose arrows are functions.
In mathematics, specifically category theory, adjunction is a relationship that two functors may exhibit, intuitively corresponding to a weak form of equivalence between two related categories. Two functors that stand in this relationship are known as adjoint functors, one being the left adjoint and the other the right adjoint. Pairs of adjoint functors are ubiquitous in mathematics and often arise from constructions of "optimal solutions" to certain problems, such as the construction of a free group on a set in algebra, or the construction of the Stone–Čech compactification of a topological space in topology.
In category theory, an epimorphism is a morphism f : X → Y that is right-cancellative in the sense that, for all objects Z and all morphisms g1, g2: Y → Z,
In mathematics, an algebraic structure consists of a nonempty set A, a collection of operations on A, and a finite set of identities, known as axioms, that these operations must satisfy.
In category theory, a branch of mathematics, an enriched category generalizes the idea of a category by replacing hom-sets with objects from a general monoidal category. It is motivated by the observation that, in many practical applications, the hom-set often has additional structure that should be respected, e.g., that of being a vector space of morphisms, or a topological space of morphisms. In an enriched category, the set of morphisms associated with every pair of objects is replaced by an object in some fixed monoidal category of "hom-objects". In order to emulate the (associative) composition of morphisms in an ordinary category, the hom-category must have a means of composing hom-objects in an associative manner: that is, there must be a binary operation on objects giving us at least the structure of a monoidal category, though in some contexts the operation may also need to be commutative and perhaps also to have a right adjoint.
In mathematics, the idea of a free object is one of the basic concepts of abstract algebra. Informally, a free object over a set A can be thought of as being a "generic" algebraic structure over A: the only equations that hold between elements of the free object are those that follow from the defining axioms of the algebraic structure. Examples include free groups, tensor algebras, or free lattices.
In mathematics, particularly category theory, a representable functor is a certain functor from an arbitrary category into the category of sets. Such functors give representations of an abstract category in terms of known structures allowing one to utilize, as much as possible, knowledge about the category of sets in other settings.
In mathematics, in the area of category theory, a forgetful functor 'forgets' or drops some or all of the input's structure or properties 'before' mapping to the output. For an algebraic structure of a given signature, this may be expressed by curtailing the signature: the new signature is an edited form of the old one. If the signature is left as an empty list, the functor is simply to take the underlying set of a structure. Because many structures in mathematics consist of a set with an additional added structure, a forgetful functor that maps to the underlying set is the most common case.
In mathematics, a simplicial set is an object composed of simplices in a specific way. Simplicial sets are higher-dimensional generalizations of directed graphs, partially ordered sets and categories. Formally, a simplicial set may be defined as a contravariant functor from the simplex category to the category of sets. Simplicial sets were introduced in 1950 by Samuel Eilenberg and Joseph A. Zilber.
This is a glossary of properties and concepts in category theory in mathematics.
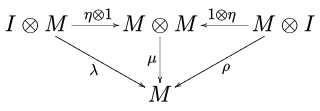
In category theory, a branch of mathematics, a monoid (or monoid object, or internal monoid, or algebra) (M, μ, η) in a monoidal category (C, ⊗, I) is an object M together with two morphisms
In mathematics, a quotient category is a category obtained from another category by identifying sets of morphisms. Formally, it is a quotient object in the category of categories, analogous to a quotient group or quotient space, but in the categorical setting.
In mathematics, the category of rings, denoted by Ring, is the category whose objects are rings and whose morphisms are ring homomorphisms. Like many categories in mathematics, the category of rings is large, meaning that the class of all rings is proper.
In mathematics, particularly in category theory, a morphism is a structure-preserving map from one mathematical structure to another one of the same type. The notion of morphism recurs in much of contemporary mathematics. In set theory, morphisms are functions; in linear algebra, linear transformations; in group theory, group homomorphisms; in analysis and topology, continuous functions, and so on.



