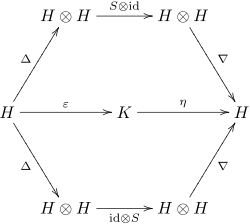
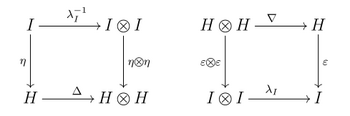
In mathematics, coalgebras or cogebras are structures that are dual to unital associative algebras. The axioms of unital associative algebras can be formulated in terms of commutative diagrams. Turning all arrows around, one obtains the axioms of coalgebras. Every coalgebra, by duality, gives rise to an algebra, but not in general the other way. In finite dimensions, this duality goes in both directions.
In mathematics, a bialgebra over a field K is a vector space over K which is both a unital associative algebra and a counital coassociative coalgebra. The algebraic and coalgebraic structures are made compatible with a few more axioms. Specifically, the comultiplication and the counit are both unital algebra homomorphisms, or equivalently, the multiplication and the unit of the algebra both are coalgebra morphisms.

In mathematics and theoretical physics, the term quantum group denotes one of a few different kinds of noncommutative algebras with additional structure. These include Drinfeld–Jimbo type quantum groups, compact matrix quantum groups, and bicrossproduct quantum groups. Despite their name, they do not themselves have a natural group structure, though they are in some sense 'close' to a group.
In mathematics, the tensor algebra of a vector space V, denoted T(V) or T•(V), is the algebra of tensors on V (of any rank) with multiplication being the tensor product. It is the free algebra on V, in the sense of being left adjoint to the forgetful functor from algebras to vector spaces: it is the "most general" algebra containing V, in the sense of the corresponding universal property (see below).
In abstract algebra, a representation of a Hopf algebra is a representation of its underlying associative algebra. That is, a representation of a Hopf algebra H over a field K is a K-vector space V with an action H × V → V usually denoted by juxtaposition ( that is, the image of (h,v) is written hv ). The vector space V is called an H-module.
In mathematics, a comodule or corepresentation is a concept dual to a module. The definition of a comodule over a coalgebra is formed by dualizing the definition of a module over an associative algebra.
In mathematics, especially in the fields of representation theory and module theory, a Frobenius algebra is a finite-dimensional unital associative algebra with a special kind of bilinear form which gives the algebras particularly nice duality theories. Frobenius algebras began to be studied in the 1930s by Richard Brauer and Cecil Nesbitt and were named after Georg Frobenius. Tadashi Nakayama discovered the beginnings of a rich duality theory, . Jean Dieudonné used this to characterize Frobenius algebras. Frobenius algebras were generalized to quasi-Frobenius rings, those Noetherian rings whose right regular representation is injective. In recent times, interest has been renewed in Frobenius algebras due to connections to topological quantum field theory.
In mathematics, a Hopf algebra, H, is quasitriangular if there exists an invertible element, R, of such that
In mathematics, compact quantum groups are generalisations of compact groups, where the commutative -algebra of continuous complex-valued functions on a compact group is generalised to an abstract structure on a not-necessarily commutative unital -algebra, which plays the role of the "algebra of continuous complex-valued functions on the compact quantum group".
In mathematics, quasi-bialgebras are a generalization of bialgebras: they were first defined by the Ukrainian mathematician Vladimir Drinfeld in 1990. A quasi-bialgebra differs from a bialgebra by having coassociativity replaced by an invertible element which controls the non-coassociativity. One of their key properties is that the corresponding category of modules forms a tensor category.
A quasi-Hopf algebra is a generalization of a Hopf algebra, which was defined by the Russian mathematician Vladimir Drinfeld in 1989.
A ribbon Hopf algebra is a quasitriangular Hopf algebra which possess an invertible central element more commonly known as the ribbon element, such that the following conditions hold:
In mathematics, a braided Hopf algebra is a Hopf algebra in a braided monoidal category. The most common braided Hopf algebras are objects in a Yetter–Drinfeld category of a Hopf algebra H, particularly the Nichols algebra of a braided vector space in that category.
In mathematics, the Butcher group, named after the New Zealand mathematician John C. Butcher by Hairer & Wanner (1974), is an infinite-dimensional Lie group first introduced in numerical analysis to study solutions of non-linear ordinary differential equations by the Runge–Kutta method. It arose from an algebraic formalism involving rooted trees that provides formal power series solutions of the differential equation modeling the flow of a vector field. It was Cayley (1857), prompted by the work of Sylvester on change of variables in differential calculus, who first noted that the derivatives of a composition of functions can be conveniently expressed in terms of rooted trees and their combinatorics.
In mathematics, Schur algebras, named after Issai Schur, are certain finite-dimensional algebras closely associated with Schur–Weyl duality between general linear and symmetric groups. They are used to relate the representation theories of those two groups. Their use was promoted by the influential monograph of J. A. Green first published in 1980. The name "Schur algebra" is due to Green. In the modular case Schur algebras were used by Gordon James and Karin Erdmann to show that the problems of computing decomposition numbers for general linear groups and symmetric groups are actually equivalent. Schur algebras were used by Friedlander and Suslin to prove finite generation of cohomology of finite group schemes.
In mathematics, in the theory of Hopf algebras, a Hopf algebroid is a generalisation of weak Hopf algebras, certain skew Hopf algebras and commutative Hopf k-algebroids. If k is a field, a commutative k-algebroid is a cogroupoid object in the category of k-algebras; the category of such is hence dual to the category of groupoid k-schemes. This commutative version has been used in 1970-s in algebraic geometry and stable homotopy theory. The generalization of Hopf algebroids and its main part of the structure, associative bialgebroids, to the noncommutative base algebra was introduced by J.-H. Lu in 1996 as a result on work on groupoids in Poisson geometry. They may be loosely thought of as Hopf algebras over a noncommutative base ring, where weak Hopf algebras become Hopf algebras over a separable algebra. It is a theorem that a Hopf algebroid satisfying a finite projectivity condition over a separable algebra is a weak Hopf algebra, and conversely a weak Hopf algebra H is a Hopf algebroid over its separable subalgebra HL. The antipode axioms have been changed by G. Böhm and K. Szlachányi in 2004 for tensor categorical reasons and to accommodate examples associated to depth two Frobenius algebra extensions.
In mathematics, weak bialgebras are a generalization of bialgebras that are both algebras and coalgebras but for which the compatibility conditions between the two structures have been "weakened". In the same spirit, weak Hopf algebras are weak bialgebras together with a linear map S satisfying specific conditions; they are generalizations of Hopf algebras.
In mathematics, if is an associative algebra over some ground field k, then a left associative -bialgebroid is another associative k-algebra together with the following additional maps: an algebra map called the source map, an algebra map called the target map, so that the elements of the images of and commute in , therefore inducing an -bimodule structure on via the rule for ; an -bimodule morphism which is required to be a counital coassociative comultiplication on in the monoidal category of -bimodules with monoidal product .
In algebraic topology, through an algebraic operation (dualization), there is an associated commutative algebra from the noncommutative Steenrod algebras called the dual Steenrod algebra. This dual algebra has a number of surprising benefits, such as being commutative and provided technical tools for computing the Adams spectral sequence in many cases with much ease.
In quantum group and Hopf algebra, the bicrossed product is a process to create new Hopf algebras from the given ones. It's motivated by the Zappa–Szép product of groups. It was first discussed by M. Takeuchi in 1981, and now a general tool for construction of Drinfeld quantum double.