
The uncertainty principle, also known as Heisenberg's indeterminacy principle, is a fundamental concept in quantum mechanics. It states that there is a limit to the precision with which certain pairs of physical properties, such as position and momentum, can be simultaneously known. In other words, the more accurately one property is measured, the less accurately the other property can be known.

The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary smooth potential can usually be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics. Furthermore, it is one of the few quantum-mechanical systems for which an exact, analytical solution is known.

A wavelet is a wave-like oscillation with an amplitude that begins at zero, increases or decreases, and then returns to zero one or more times. Wavelets are termed a "brief oscillation". A taxonomy of wavelets has been established, based on the number and direction of its pulses. Wavelets are imbued with specific properties that make them useful for signal processing.

In physics, engineering and mathematics, the Fourier transform (FT) is an integral transform that takes a function as input and outputs another function that describes the extent to which various frequencies are present in the original function. The output of the transform is a complex-valued function of frequency. The term Fourier transform refers to both this complex-valued function and the mathematical operation. When a distinction needs to be made the Fourier transform is sometimes called the frequency domain representation of the original function. The Fourier transform is analogous to decomposing the sound of a musical chord into the intensities of its constituent pitches.
In mathematics, the Hermite polynomials are a classical orthogonal polynomial sequence.
In mathematics, a Gaussian function, often simply referred to as a Gaussian, is a function of the base form

In mathematics, the digamma function is defined as the logarithmic derivative of the gamma function:

In physics, a wave packet is a short burst of localized wave action that travels as a unit, outlined by an envelope. A wave packet can be analyzed into, or can be synthesized from, a potentially-infinite set of component sinusoidal waves of different wavenumbers, with phases and amplitudes such that they interfere constructively only over a small region of space, and destructively elsewhere. Any signal of a limited width in time or space requires many frequency components around a center frequency within a bandwidth inversely proportional to that width; even a gaussian function is considered a wave packet because its Fourier transform is a "packet" of waves of frequencies clustered around a central frequency. Each component wave function, and hence the wave packet, are solutions of a wave equation. Depending on the wave equation, the wave packet's profile may remain constant or it may change while propagating.
The Gram–Charlier A series, and the Edgeworth series are series that approximate a probability distribution in terms of its cumulants. The series are the same; but, the arrangement of terms differ. The key idea of these expansions is to write the characteristic function of the distribution whose probability density function f is to be approximated in terms of the characteristic function of a distribution with known and suitable properties, and to recover f through the inverse Fourier transform.

In numerical analysis and functional analysis, a discrete wavelet transform (DWT) is any wavelet transform for which the wavelets are discretely sampled. As with other wavelet transforms, a key advantage it has over Fourier transforms is temporal resolution: it captures both frequency and location information.

In mathematics and numerical analysis, the Ricker wavelet
In applied mathematics, the complex Mexican hat wavelet is a low-oscillation, complex-valued, wavelet for the continuous wavelet transform. This wavelet is formulated in terms of its Fourier transform as the Hilbert analytic signal of the conventional Mexican hat wavelet:

In algebra, the Bring radical or ultraradical of a real number a is the unique real root of the polynomial

In mathematics, a wavelet series is a representation of a square-integrable function by a certain orthonormal series generated by a wavelet. This article provides a formal, mathematical definition of an orthonormal wavelet and of the integral wavelet transform.
In functional analysis, the Shannon wavelet is a decomposition that is defined by signal analysis by ideal bandpass filters. Shannon wavelet may be either of real or complex type.
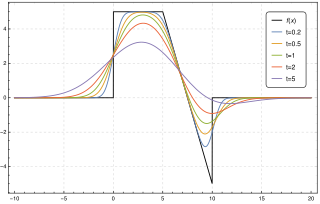
In mathematics, the Weierstrass transform of a function f : R → R, named after Karl Weierstrass, is a "smoothed" version of f(x) obtained by averaging the values of f, weighted with a Gaussian centered at x.
The Mehler kernel is a complex-valued function found to be the propagator of the quantum harmonic oscillator.
The wavelet transform modulus maxima (WTMM) is a method for detecting the fractal dimension of a signal.
Fractional wavelet transform (FRWT) is a generalization of the classical wavelet transform (WT). This transform is proposed in order to rectify the limitations of the WT and the fractional Fourier transform (FRFT). The FRWT inherits the advantages of multiresolution analysis of the WT and has the capability of signal representations in the fractional domain which is similar to the FRFT.
In mathematics, in functional analysis, several different wavelets are known by the name Poisson wavelet. In one context, the term "Poisson wavelet" is used to denote a family of wavelets labeled by the set of positive integers, the members of which are associated with the Poisson probability distribution. These wavelets were first defined and studied by Karlene A. Kosanovich, Allan R. Moser and Michael J. Piovoso in 1995–96. In another context, the term refers to a certain wavelet which involves a form of the Poisson integral kernel. In still another context, the terminology is used to describe a family of complex wavelets indexed by positive integers which are connected with the derivatives of the Poisson integral kernel.




























