
A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e. an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is radially equilateral.

In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Expressed algebraically, for quantities and with ,

In geometry, an octahedron is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.

A Pythagorean triple consists of three positive integers a, b, and c, such that a2 + b2 = c2. Such a triple is commonly written (a, b, c), and a well-known example is (3, 4, 5). If (a, b, c) is a Pythagorean triple, then so is (ka, kb, kc) for any positive integer k. A primitive Pythagorean triple is one in which a, b and c are coprime (that is, they have no common divisor larger than 1). For example, (3, 4, 5) is a primitive Pythagorean triple whereas (6, 8, 10) is not. A triangle whose sides form a Pythagorean triple is called a Pythagorean triangle, and is necessarily a right triangle.

In geometry, a tetrahedron, also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the ordinary convex polyhedra.

A right triangle or right-angled triangle (British), or more formally an orthogonal triangle, formerly called a rectangled triangle, is a triangle in which one angle is a right angle, i.e., in which two sides are perpendicular. The relation between the sides and other angles of the right triangle is the basis for trigonometry.
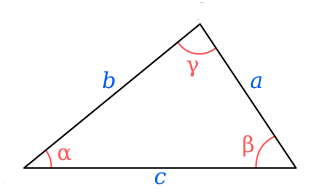
In geometry, Heron's formula gives the area of a triangle in terms of the three side lengths a, b, c. If is the semiperimeter of the triangle, the area A is,

In geometry, an isosceles triangle is a triangle that has two sides of equal length. Sometimes it is specified as having exactly two sides of equal length, and sometimes as having at least two sides of equal length, the latter version thus including the equilateral triangle as a special case. Examples of isosceles triangles include the isosceles right triangle, the golden triangle, and the faces of bipyramids and certain Catalan solids.

In geometry, the triangular bipyramid is a type of hexahedron, being the first in the infinite set of face-transitive bipyramids. It is the dual of the triangular prism with 6 isosceles triangle faces.
In geometry, a Heronian triangle is a triangle whose side lengths a, b, and c and area A are all positive integers. Heronian triangles are named after Heron of Alexandria, based on their relation to Heron's formula which Heron demonstrated with the example triangle of sides 13, 14, 15 and area 84.

In geometry, a median of a triangle is a line segment joining a vertex to the midpoint of the opposite side, thus bisecting that side. Every triangle has exactly three medians, one from each vertex, and they all intersect each other at the triangle's centroid. In the case of isosceles and equilateral triangles, a median bisects any angle at a vertex whose two adjacent sides are equal in length. The concept of a median extends to tetrahedra.
In mathematics, an Euler brick, named after Leonhard Euler, is a rectangular cuboid whose edges and face diagonals all have integer lengths. A primitive Euler brick is an Euler brick whose edge lengths are relatively prime. A perfect Euler brick is one whose space diagonal is also an integer but such a brick has not yet been found.

A special right triangle is a right triangle with some regular feature that makes calculations on the triangle easier, or for which simple formulas exist. For example, a right triangle may have angles that form simple relationships, such as 45°–45°–90°. This is called an "angle-based" right triangle. A "side-based" right triangle is one in which the lengths of the sides form ratios of whole numbers, such as 3 : 4 : 5, or of other special numbers such as the golden ratio. Knowing the relationships of the angles or ratios of sides of these special right triangles allows one to quickly calculate various lengths in geometric problems without resorting to more advanced methods.

In geometry, a disphenoid is a tetrahedron whose four faces are congruent acute-angled triangles. It can also be described as a tetrahedron in which every two edges that are opposite each other have equal lengths. Other names for the same shape are isotetrahedron, sphenoid, bisphenoid, isosceles tetrahedron, equifacial tetrahedron, almost regular tetrahedron, and tetramonohedron.
A two-dimensional equable shape is one whose area is numerically equal to its perimeter. For example, a right angled triangle with sides 5, 12 and 13 has area and perimeter both have a unitless numerical value of 30.
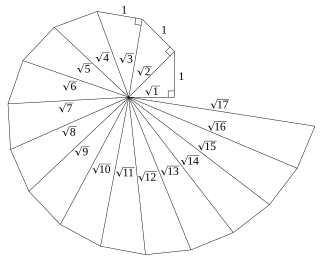
In geometry, the spiral of Theodorus is a spiral composed of right triangles, placed edge-to-edge. It was named after Theodorus of Cyrene.

An integer triangle or integral triangle is a triangle all of whose side lengths are integers. A rational triangle is one whose side lengths are rational numbers; any rational triangle can be rescaled by the lowest common denominator of the sides to obtain a similar integer triangle, so there is a close relationship between integer triangles and rational triangles.

In plane geometry, an automedian triangle is a triangle in which the lengths of the three medians are proportional to the lengths of the three sides, in a different order. The three medians of an automedian triangle may be translated to form the sides of a second triangle that is similar to the first one.

In geometry, a trirectangular tetrahedron is a tetrahedron where all three face angles at one vertex are right angles. That vertex is called the right angle of the trirectangular tetrahedron and the face opposite it is called the base. The three edges that meet at the right angle are called the legs and the perpendicular from the right angle to the base is called the altitude of the tetrahedron.
Pythagorean Triangles is a book on right triangles, the Pythagorean theorem, and Pythagorean triples. It was originally written in the Polish language by Wacław Sierpiński, and published in Warsaw in 1954. Indian mathematician Ambikeshwar Sharma translated it into English, with some added material from Sierpiński, and published it in the Scripta Mathematica Studies series of Yeshiva University in 1962. Dover Books republished the translation in a paperback edition in 2003. There is also a Russian translation of the 1954 edition.

























