
The uncertainty principle, also known as Heisenberg's indeterminacy principle, is a fundamental concept in quantum mechanics. It states that there is a limit to the precision with which certain pairs of physical properties, such as position and momentum, can be simultaneously known. In other words, the more accurately one property is measured, the less accurately the other property can be known.
Shor's algorithm is a quantum algorithm for finding the prime factors of an integer. It was developed in 1994 by the American mathematician Peter Shor. It is one of the few known quantum algorithms with compelling potential applications and strong evidence of superpolynomial speedup compared to best known classical algorithms. On the other hand, factoring numbers of practical significance requires far more qubits than available in the near future. Another concern is that noise in quantum circuits may undermine results, requiring additional qubits for quantum error correction.
In quantum computing, Grover's algorithm, also known as the quantum search algorithm, is a quantum algorithm for unstructured search that finds with high probability the unique input to a black box function that produces a particular output value, using just evaluations of the function, where is the size of the function's domain. It was devised by Lov Grover in 1996.
The Riemann hypothesis is one of the most important conjectures in mathematics. It is a statement about the zeros of the Riemann zeta function. Various geometrical and arithmetical objects can be described by so-called global L-functions, which are formally similar to the Riemann zeta-function. One can then ask the same question about the zeros of these L-functions, yielding various generalizations of the Riemann hypothesis. Many mathematicians believe these generalizations of the Riemann hypothesis to be true. The only cases of these conjectures which have been proven occur in the algebraic function field case.
The Deutsch–Jozsa algorithm is a deterministic quantum algorithm proposed by David Deutsch and Richard Jozsa in 1992 with improvements by Richard Cleve, Artur Ekert, Chiara Macchiavello, and Michele Mosca in 1998. Although of little practical use, it is one of the first examples of a quantum algorithm that is exponentially faster than any possible deterministic classical algorithm.
In quantum mechanics, a Slater determinant is an expression that describes the wave function of a multi-fermionic system. It satisfies anti-symmetry requirements, and consequently the Pauli principle, by changing sign upon exchange of two electrons. Only a small subset of all possible fermionic wave functions can be written as a single Slater determinant, but those form an important and useful subset because of their simplicity.
In quantum computing, a quantum algorithm is an algorithm which runs on a realistic model of quantum computation, the most commonly used model being the quantum circuit model of computation. A classical algorithm is a finite sequence of instructions, or a step-by-step procedure for solving a problem, where each step or instruction can be performed on a classical computer. Similarly, a quantum algorithm is a step-by-step procedure, where each of the steps can be performed on a quantum computer. Although all classical algorithms can also be performed on a quantum computer, the term quantum algorithm is usually used for those algorithms which seem inherently quantum, or use some essential feature of quantum computation such as quantum superposition or quantum entanglement.
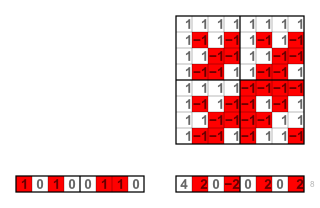
The Hadamard transform is an example of a generalized class of Fourier transforms. It performs an orthogonal, symmetric, involutive, linear operation on 2m real numbers.
In group theory, a branch of abstract algebra, a character table is a two-dimensional table whose rows correspond to irreducible representations, and whose columns correspond to conjugacy classes of group elements. The entries consist of characters, the traces of the matrices representing group elements of the column's class in the given row's group representation. In chemistry, crystallography, and spectroscopy, character tables of point groups are used to classify e.g. molecular vibrations according to their symmetry, and to predict whether a transition between two states is forbidden for symmetry reasons. Many university level textbooks on physical chemistry, quantum chemistry, spectroscopy and inorganic chemistry devote a chapter to the use of symmetry group character tables.

In mathematics, Burnside's theorem in group theory states that if G is a finite group of order where p and q are prime numbers, and a and b are non-negative integers, then G is solvable. Hence each non-Abelian finite simple group has order divisible by at least three distinct primes.
In computational complexity theory, PostBQP is a complexity class consisting of all of the computational problems solvable in polynomial time on a quantum Turing machine with postselection and bounded error.
The time-evolving block decimation (TEBD) algorithm is a numerical scheme used to simulate one-dimensional quantum many-body systems, characterized by at most nearest-neighbour interactions. It is dubbed Time-evolving Block Decimation because it dynamically identifies the relevant low-dimensional Hilbert subspaces of an exponentially larger original Hilbert space. The algorithm, based on the Matrix Product States formalism, is highly efficient when the amount of entanglement in the system is limited, a requirement fulfilled by a large class of quantum many-body systems in one dimension.
In computational complexity theory and quantum computing, Simon's problem is a computational problem that is proven to be solved exponentially faster on a quantum computer than on a classical computer. The quantum algorithm solving Simon's problem, usually called Simon's algorithm, served as the inspiration for Shor's algorithm. Both problems are special cases of the abelian hidden subgroup problem, which is now known to have efficient quantum algorithms.
Quantum walks are quantum analogues of classical random walks. In contrast to the classical random walk, where the walker occupies definite states and the randomness arises due to stochastic transitions between states, in quantum walks randomness arises through: (1) quantum superposition of states, (2) non-random, reversible unitary evolution and (3) collapse of the wave function due to state measurements.
Amplitude amplification is a technique in quantum computing which generalizes the idea behind Grover's search algorithm, and gives rise to a family of quantum algorithms. It was discovered by Gilles Brassard and Peter Høyer in 1997, and independently rediscovered by Lov Grover in 1998.
In cryptography, Learning with errors (LWE) is a mathematical problem that is widely used in cryptography to create secure encryption algorithms. It is based on the idea of representing secret information as a set of equations with errors. In other words, LWE is a way to hide the value of a secret by introducing noise to it. In more technical terms, it refers to the computational problem of inferring a linear -ary function over a finite ring from given samples some of which may be erroneous. The LWE problem is conjectured to be hard to solve, and thus to be useful in cryptography.
In quantum computing, the quantum Fourier transform (QFT) is a linear transformation on quantum bits, and is the quantum analogue of the discrete Fourier transform. The quantum Fourier transform is a part of many quantum algorithms, notably Shor's algorithm for factoring and computing the discrete logarithm, the quantum phase estimation algorithm for estimating the eigenvalues of a unitary operator, and algorithms for the hidden subgroup problem. The quantum Fourier transform was discovered by Don Coppersmith.

A Matrix product state (MPS) is a quantum state of many particles, written in the following form:
Quantum counting algorithm is a quantum algorithm for efficiently counting the number of solutions for a given search problem. The algorithm is based on the quantum phase estimation algorithm and on Grover's search algorithm.

The Bernstein–Vazirani algorithm, which solves the Bernstein–Vazirani problem, is a quantum algorithm invented by Ethan Bernstein and Umesh Vazirani in 1997. It is a restricted version of the Deutsch–Jozsa algorithm where instead of distinguishing between two different classes of functions, it tries to learn a string encoded in a function. The Bernstein–Vazirani algorithm was designed to prove an oracle separation between complexity classes BQP and BPP.




























































