Klein paradox

Last updated April 01, 2024

In 1929, physicist Oskar Klein ^[1] obtained a surprising result by applying the Dirac equation to the familiar problem of electron scattering from a potential barrier. In nonrelativistic quantum mechanics, electron tunneling into a barrier is observed, with exponential damping. However, Klein's result showed that if the potential is at least of the order of the electron mass, $Ve\sim mc^{2}$ , the barrier is nearly transparent. Moreover, as the potential approaches infinity, the reflection diminishes and the electron is always transmitted.

The immediate application of the paradox was to Rutherford's proton–electron model for neutral particles within the nucleus, before the discovery of the neutron. The paradox presented a quantum mechanical objection to the notion of an electron confined within a nucleus.^[2] This clear and precise paradox suggested that an electron could not be confined within a nucleus by any potential well. The meaning of this paradox was intensely debated at the time.^[2]

Massless particles

Consider a massless relativistic particle approaching a potential step of height $V_{0}$ with energy $E_{0}<V_{0}e$ and momentum $p$ .

The particle's wave function, $\psi$ , follows the time-independent Dirac equation:

\left(\sigma _{x}p+V\right)\psi =E_{0}\psi ,\quad V={\begin{cases}0,&x<0\\V_{0},&x>0\end{cases}}

And $\sigma _{x}$ is the Pauli matrix:

\sigma _{x}=\left({\begin{matrix}0&1\\1&0\end{matrix}}\right)

Fig. 1 A depiction of the dispersion relation, the x-axis represents momentum while the y-axis represents energy. Dispersion1.png — Fig. 1 A depiction of the dispersion relation, the x-axis represents momentum while the y-axis represents energy.

Assuming the particle is propagating from the left, we obtain two solutions — one before the step, in region (1) and one under the potential, in region (2):

\psi _{1}=Ae^{ipx}\left({\begin{matrix}1\\1\end{matrix}}\right)+A'e^{-ipx}\left({\begin{matrix}-1\\1\end{matrix}}\right),\quad p=E_{0}\,

\psi _{2}=Be^{ikx}\left({\begin{matrix}1\\1\end{matrix}}\right),\quad \left|k\right|=V_{0}-E_{0}\,

where the coefficients $A$ , $A'$ and $B$ are complex numbers. Both the incoming and transmitted wave functions are associated with positive group velocity (Blue lines in Fig.1), whereas the reflected wave function is associated with negative group velocity. (Green lines in Fig.1)

We now want to calculate the transmission and reflection coefficients, $T,R.$ They are derived from the probability amplitude currents.

The definition of the probability current associated with the Dirac equation is:

J_{i}=\psi _{i}^{\dagger }\sigma _{x}\psi _{i},\ i=1,2\,

In this case:

J_{1}=2\left[\left|A\right|^{2}-\left|A'\right|^{2}\right],\quad J_{2}=2\left|B\right|^{2}\,

The transmission and reflection coefficients are:

R={\frac {\left|A'\right|^{2}}{\left|A\right|^{2}}},\quad T={\frac {\left|B\right|^{2}}{\left|A\right|^{2}}}\,

Continuity of the wave function at $x=0$ , yields:

\left|A\right|^{2}=\left|B\right|^{2}\,

\left|A'\right|^{2}=0\,

And so the transmission coefficient is 1 and there is no reflection.

One interpretation of the paradox is that a potential step cannot reverse the direction of the group velocity of a massless relativistic particle. This explanation best suits the single particle solution cited above. Other, more complex interpretations are suggested in literature, in the context of quantum field theory where the unrestrained tunnelling is shown to occur due to the existence of particle–antiparticle pairs at the potential.

Massive case

For the massive case, the calculations are similar to the above. The results are as surprising as in the massless case. The transmission coefficient is always larger than zero, and approaches 1 as the potential step goes to infinity.

The Klein zone

If the energy of the particle is in the range $mc^{2}<E<Ve-mc^{2}$ , then partial reflection rather than total reflection will result.

Resolutions for the massive case

While the traditional resolution uses particle–anti-particle pair production in the context of quantum field theory (Hansen 1981), a simpler resolution exists that substitutes physical pair production for the scattering of negative energy solutions under the barrier (Alhaidari 2009). This strategy was also applied to obtain analytic solutions to the Dirac equation for an infinite square well.

Other cases

These results were expanded to higher dimensions, and to other types of potentials, such as a linear step, a square barrier, a smooth potential, etc. Many experiments in electron transport in graphene rely on the Klein paradox for massless particles.^[3]^[4]

Related Research Articles

In particle physics, the Dirac equation is a relativistic wave equation derived by British physicist Paul Dirac in 1928. In its free form, or including electromagnetic interactions, it describes all spin-1⁄2 massive particles, called "Dirac particles", such as electrons and quarks for which parity is a symmetry. It is consistent with both the principles of quantum mechanics and the theory of special relativity, and was the first theory to account fully for special relativity in the context of quantum mechanics. It was validated by accounting for the fine structure of the hydrogen spectrum in a completely rigorous way.

The Schrödinger equation is a linear partial differential equation that governs the wave function of a quantum-mechanical system. Its discovery was a significant landmark in the development of quantum mechanics. It is named after Erwin Schrödinger, who postulated the equation in 1925 and published it in 1926, forming the basis for the work that resulted in his Nobel Prize in Physics in 1933.

In physics, charge conjugation is a transformation that switches all particles with their corresponding antiparticles, thus changing the sign of all charges: not only electric charge but also the charges relevant to other forces. The term C-symmetry is an abbreviation of the phrase "charge conjugation symmetry", and is used in discussions of the symmetry of physical laws under charge-conjugation. Other important discrete symmetries are P-symmetry (parity) and T-symmetry.

The Klein–Gordon equation is a relativistic wave equation, related to the Schrödinger equation. It is second-order in space and time and manifestly Lorentz-covariant. It is a differential equation version of the relativistic energy–momentum relation $.$

The Dirac sea is a theoretical model of the electron vacuum as an infinite sea of electrons with negative energy, now called positrons. It was first postulated by the British physicist Paul Dirac in 1930 to explain the anomalous negative-energy quantum states predicted by the Dirac equation for relativistic electrons. The positron, the antimatter counterpart of the electron, was originally conceived of as a hole in the Dirac sea, before its experimental discovery in 1932.

In physics, specifically relativistic quantum mechanics (RQM) and its applications to particle physics, relativistic wave equations predict the behavior of particles at high energies and velocities comparable to the speed of light. In the context of quantum field theory (QFT), the equations determine the dynamics of quantum fields. The solutions to the equations, universally denoted as $ψ$ or $Ψ$ , are referred to as "wave functions" in the context of RQM, and "fields" in the context of QFT. The equations themselves are called "wave equations" or "field equations", because they have the mathematical form of a wave equation or are generated from a Lagrangian density and the field-theoretic Euler–Lagrange equations.

In physics, the S-matrix or scattering matrix relates the initial state and the final state of a physical system undergoing a scattering process. It is used in quantum mechanics, scattering theory and quantum field theory (QFT).

In physics, quantum tunnelling, barrier penetration, or simply tunnelling is a quantum mechanical phenomenon in which an object such as an electron or atom passes through a potential energy barrier that, according to classical mechanics, should not be passable due to the object not having sufficient energy to pass or surmount the barrier.

The Compton wavelength is a quantum mechanical property of a particle, defined as the wavelength of a photon the energy of which is the same as the rest energy of that particle. It was introduced by Arthur Compton in 1923 in his explanation of the scattering of photons by electrons.

In atomic physics, the electron magnetic moment, or more specifically the electron magnetic dipole moment, is the magnetic moment of an electron resulting from its intrinsic properties of spin and electric charge. The value of the electron magnetic moment is −9.2847647043(28)×10⁻²⁴ J⋅T⁻¹. In units of the Bohr magneton (μ_B), it is −1.00115965218059(13) μ_B, a value that was measured with a relative accuracy of 1.3×10⁻¹³.

In physics, the zitterbewegung (German pronunciation:[ˈtsɪtɐ.bəˌveːɡʊŋ], from German zittern 'to tremble, jitter', and Bewegung 'motion') is the theoretical prediction of a rapid oscillatory motion of elementary particles that obey relativistic wave equations. This prediction was first discussed by Gregory Breit in 1928 and later by Erwin Schrödinger in 1930 as a result of analysis of the wave packet solutions of the Dirac equation for relativistic electrons in free space, in which an interference between positive and negative energy states produces an apparent fluctuation (up to the speed of light) of the position of an electron around the median, with an angular frequency of $2 mc 2 / ℏ$ , or approximately 1.6×10²¹ radians per second.

This article describes the mathematics of the Standard Model of particle physics, a gauge quantum field theory containing the internal symmetries of the unitary product group $SU(3) \times SU(2) \times U(1)$ . The theory is commonly viewed as describing the fundamental set of particles – the leptons, quarks, gauge bosons and the Higgs boson.

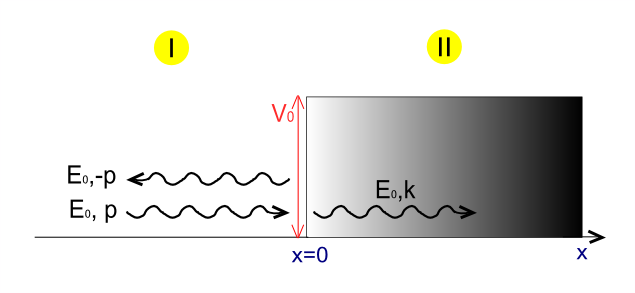
In quantum mechanics and scattering theory, the one-dimensional step potential is an idealized system used to model incident, reflected and transmitted matter waves. The problem consists of solving the time-independent Schrödinger equation for a particle with a step-like potential in one dimension. Typically, the potential is modeled as a Heaviside step function.

In quantum mechanics, the rectangularpotential barrier is a standard one-dimensional problem that demonstrates the phenomena of wave-mechanical tunneling and wave-mechanical reflection. The problem consists of solving the one-dimensional time-independent Schrödinger equation for a particle encountering a rectangular potential energy barrier. It is usually assumed, as here, that a free particle impinges on the barrier from the left.

In quantum mechanics, the energies of cyclotron orbits of charged particles in a uniform magnetic field are quantized to discrete values, called Landau levels. These levels are degenerate, with the number of electrons per level directly proportional to the strength of the applied magnetic field. It is named after the Soviet physicist Lev Landau.

In quantum mechanics the delta potential is a potential well mathematically described by the Dirac delta function - a generalized function. Qualitatively, it corresponds to a potential which is zero everywhere, except at a single point, where it takes an infinite value. This can be used to simulate situations where a particle is free to move in two regions of space with a barrier between the two regions. For example, an electron can move almost freely in a conducting material, but if two conducting surfaces are put close together, the interface between them acts as a barrier for the electron that can be approximated by a delta potential.

In quantum mechanics, the Pauli equation or Schrödinger–Pauli equation is the formulation of the Schrödinger equation for spin-½ particles, which takes into account the interaction of the particle's spin with an external electromagnetic field. It is the non-relativistic limit of the Dirac equation and can be used where particles are moving at speeds much less than the speed of light, so that relativistic effects can be neglected. It was formulated by Wolfgang Pauli in 1927. In its linearized form it is known as Lévy-Leblond equation.

In physics, relativistic quantum mechanics (RQM) is any Poincaré covariant formulation of quantum mechanics (QM). This theory is applicable to massive particles propagating at all velocities up to those comparable to the speed of light c, and can accommodate massless particles. The theory has application in high energy physics, particle physics and accelerator physics, as well as atomic physics, chemistry and condensed matter physics. Non-relativistic quantum mechanics refers to the mathematical formulation of quantum mechanics applied in the context of Galilean relativity, more specifically quantizing the equations of classical mechanics by replacing dynamical variables by operators. Relativistic quantum mechanics (RQM) is quantum mechanics applied with special relativity. Although the earlier formulations, like the Schrödinger picture and Heisenberg picture were originally formulated in a non-relativistic background, a few of them also work with special relativity.

The term Dirac matter refers to a class of condensed matter systems which can be effectively described by the Dirac equation. Even though the Dirac equation itself was formulated for fermions, the quasi-particles present within Dirac matter can be of any statistics. As a consequence, Dirac matter can be distinguished in fermionic, bosonic or anyonic Dirac matter. Prominent examples of Dirac matter are graphene and other Dirac semimetals, topological insulators, Weyl semimetals, various high-temperature superconductors with $-wave pairing and liquid helium-3. The effective theory of such systems is classified by a specific choice of the Dirac mass, the Dirac velocity, the gamma matrices and the space-time curvature. The universal treatment of the class of Dirac matter in terms of an effective theory leads to a common features with respect to the density of states, the heat capacity and impurity scattering.$

In quantum mechanics, the Lévy-Leblond equation describes the dynamics of a spin-1/2 particle. It is a linearized version of the Schrödinger equation and of the Pauli equation. It was derived by French physicist Jean-Marc Lévy-Leblond in 1967.

References

↑ Klein, O. (1929). "Die Reflexion von Elektronen an einem Potentialsprung nach der relativistischen Dynamik von Dirac". Zeitschrift für Physik. 53 (3–4): 157–165. Bibcode:1929ZPhy...53..157K. doi:10.1007/BF01339716. S2CID 121771000.
1 2 Stuewer, Roger H. (1985). "Niels Bohr and Nuclear Physics" . In French, A. P.; Kennedy, P. J. (eds.). Niels Bohr: A Centenary Volume. Harvard University Press. pp. 197–220. ISBN 0674624165.
↑ Katsnelson, M. I.; Novoselov, K. S.; Geim, A. K. (2006). "Chiral tunnelling and the Klein paradox in graphene". Nature Physics. 2 (9): 620–625. arXiv: cond-mat/0604323 . Bibcode:2006NatPh...2..620K. doi:10.1038/nphys384. S2CID 3472119.
↑ Pendry, J. B. (2007). "PHYSICS: Negative Refraction for Electrons?". Science. 315 (5816): 1226–7. doi:10.1126/science.1140178. PMID 17332397. S2CID 122548440.