
In mathematics, a diffeomorphism is an isomorphism of differentiable manifolds. It is an invertible function that maps one differentiable manifold to another such that both the function and its inverse are continuously differentiable.

In mathematics and more specifically in topology, a homeomorphism, also called topological isomorphism, or bicontinuous function, is a bijective and continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are the mappings that preserve all the topological properties of a given space. Two spaces with a homeomorphism between them are called homeomorphic, and from a topological viewpoint they are the same.
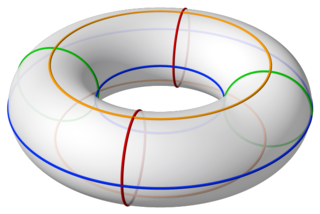
In geometry, a torus is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanar with the circle. The main types of toruses include ring toruses, horn toruses, and spindle toruses. A ring torus is sometimes colloquially referred to as a donut or doughnut.
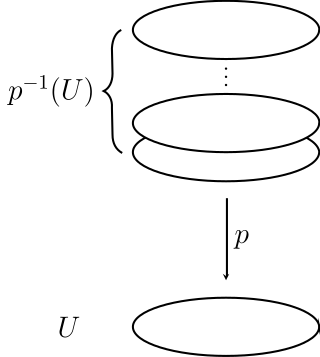
In topology, a covering or covering projection is a map between topological spaces that, intuitively, locally acts like a projection of multiple copies of a space onto itself. In particular, coverings are special types of local homeomorphisms. If is a covering, is said to be a covering space or cover of , and is said to be the base of the covering, or simply the base. By abuse of terminology, and may sometimes be called covering spaces as well. Since coverings are local homeomorphisms, a covering space is a special kind of étale space.
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, denoted which records information about loops in a space. Intuitively, homotopy groups record information about the basic shape, or holes, of a topological space.

In mathematics, cobordism is a fundamental equivalence relation on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold. Two manifolds of the same dimension are cobordant if their disjoint union is the boundary of a compact manifold one dimension higher.

In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.

In mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines through the origin of a complex Euclidean space (see below for an intuitive account). Formally, a complex projective space is the space of complex lines through the origin of an (n+1)-dimensional complex vector space. The space is denoted variously as P(Cn+1), Pn(C) or CPn. When n = 1, the complex projective space CP1 is the Riemann sphere, and when n = 2, CP2 is the complex projective plane (see there for a more elementary discussion).
In mathematics, real projective space, denoted or is the topological space of lines passing through the origin 0 in the real space It is a compact, smooth manifold of dimension n, and is a special case of a Grassmannian space.

In mathematics, the Whitehead manifold is an open 3-manifold that is contractible, but not homeomorphic to J. H. C. Whitehead discovered this puzzling object while he was trying to prove the Poincaré conjecture, correcting an error in an earlier paper Whitehead where he incorrectly claimed that no such manifold exists.
In mathematics, a spherical 3-manifoldM is a 3-manifold of the form
In mathematics, a 4-manifold is a 4-dimensional topological manifold. A smooth 4-manifold is a 4-manifold with a smooth structure. In dimension four, in marked contrast with lower dimensions, topological and smooth manifolds are quite different. There exist some topological 4-manifolds which admit no smooth structure, and even if there exists a smooth structure, it need not be unique.

In mathematics, triangulation describes the replacement of topological spaces by piecewise linear spaces, i.e. the choice of a homeomorphism in a suitable simplicial complex. Spaces being homeomorphic to a simplicial complex are called triangulable. Triangulation has various uses in different branches of mathematics, for instance in algebraic topology, in complex analysis or in modeling.
In topology, a branch of mathematics, a topological manifold is a topological space that locally resembles real n-dimensional Euclidean space. Topological manifolds are an important class of topological spaces, with applications throughout mathematics. All manifolds are topological manifolds by definition. Other types of manifolds are formed by adding structure to a topological manifold. Every manifold has an "underlying" topological manifold, obtained by simply "forgetting" the added structure. However, not every topological manifold can be endowed with a particular additional structure. For example, the E8 manifold is a topological manifold which cannot be endowed with a differentiable structure.
The Hauptvermutung of geometric topology is a now refuted conjecture asking whether any two triangulations of a triangulable space have subdivisions that are combinatorially equivalent, i.e. the subdivided triangulations are built up in the same combinatorial pattern. It was originally formulated as a conjecture in 1908 by Ernst Steinitz and Heinrich Franz Friedrich Tietze, but it is now known to be false.
In mathematics, a Hilbert manifold is a manifold modeled on Hilbert spaces. Thus it is a separable Hausdorff space in which each point has a neighbourhood homeomorphic to an infinite dimensional Hilbert space. The concept of a Hilbert manifold provides a possibility of extending the theory of manifolds to infinite-dimensional setting. Analogous to the finite-dimensional situation, one can define a differentiable Hilbert manifold by considering a maximal atlas in which the transition maps are differentiable.
In mathematics, quaternionic projective space is an extension of the ideas of real projective space and complex projective space, to the case where coordinates lie in the ring of quaternions Quaternionic projective space of dimension n is usually denoted by
In mathematics, specifically geometric topology, the Borel conjecture asserts that an aspherical closed manifold is determined by its fundamental group, up to homeomorphism. It is a rigidity conjecture, asserting that a weak, algebraic notion of equivalence should imply a stronger, topological notion.
In mathematics, Reidemeister torsion is a topological invariant of manifolds introduced by Kurt Reidemeister for 3-manifolds and generalized to higher dimensions by Wolfgang Franz and Georges de Rham . Analytic torsion is an invariant of Riemannian manifolds defined by Daniel B. Ray and Isadore M. Singer as an analytic analogue of Reidemeister torsion. Jeff Cheeger and Werner Müller proved Ray and Singer's conjecture that Reidemeister torsion and analytic torsion are the same for compact Riemannian manifolds.
This is a glossary of properties and concepts in algebraic topology in mathematics.












































